No CrossRef data available.
Article contents
MUCHNIK DEGREES AND CARDINAL CHARACTERISTICS
Published online by Cambridge University Press: 04 September 2020
Abstract
A mass problem is a set of functions 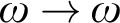 $\omega \to \omega $. For mass problems
$\omega \to \omega $. For mass problems 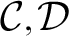 ${\mathcal {C}}, {\mathcal {D}}$, one says that
${\mathcal {C}}, {\mathcal {D}}$, one says that 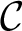 ${\mathcal {C}}$ is Muchnik reducible to
${\mathcal {C}}$ is Muchnik reducible to 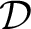 ${\mathcal {D}}$ if each function in
${\mathcal {D}}$ if each function in 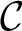 ${\mathcal {C}}$ is computed by a function in
${\mathcal {C}}$ is computed by a function in 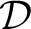 ${\mathcal {D}}$. In this paper we study some highness properties of Turing oracles, which we view as mass problems. We compare them with respect to Muchnik reducibility and its uniform strengthening, Medvedev reducibility.
${\mathcal {D}}$. In this paper we study some highness properties of Turing oracles, which we view as mass problems. We compare them with respect to Muchnik reducibility and its uniform strengthening, Medvedev reducibility.
For 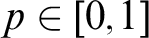 $p \in [0,1]$ let
$p \in [0,1]$ let 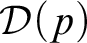 ${\mathcal {D}}(p)$ be the mass problem of infinite bit sequences y (i.e.,
${\mathcal {D}}(p)$ be the mass problem of infinite bit sequences y (i.e., 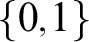 $\{0,1\}$-valued functions) such that for each computable bit sequence x, the bit sequence
$\{0,1\}$-valued functions) such that for each computable bit sequence x, the bit sequence 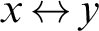 $ x {\,\leftrightarrow\,} y$ has asymptotic lower density at most p (where
$ x {\,\leftrightarrow\,} y$ has asymptotic lower density at most p (where 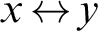 $x {\,\leftrightarrow\,} y$ has a
$x {\,\leftrightarrow\,} y$ has a 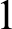 $1$ in position n iff
$1$ in position n iff 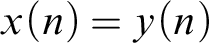 $x(n) = y(n)$). We show that all members of this family of mass problems parameterized by a real p with
$x(n) = y(n)$). We show that all members of this family of mass problems parameterized by a real p with 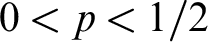 $0 < p <1/2 $ have the same complexity in the sense of Muchnik reducibility. We prove this by showing Muchnik equivalence of the problems
$0 < p <1/2 $ have the same complexity in the sense of Muchnik reducibility. We prove this by showing Muchnik equivalence of the problems 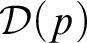 ${\mathcal {D}}(p)$ with the mass problem
${\mathcal {D}}(p)$ with the mass problem 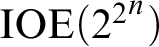 $\text {IOE}({2^{2}}^{n})$; here for an order function h, the mass problem
$\text {IOE}({2^{2}}^{n})$; here for an order function h, the mass problem 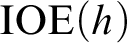 $\text {IOE}(h)$ consists of the functions f that agree infinitely often with each computable function bounded by h. This result also yields a new version of the proof to of the affirmative answer to the “Gamma question” due to the first author:
$\text {IOE}(h)$ consists of the functions f that agree infinitely often with each computable function bounded by h. This result also yields a new version of the proof to of the affirmative answer to the “Gamma question” due to the first author: 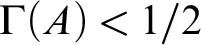 $\Gamma (A)< 1/2$ implies
$\Gamma (A)< 1/2$ implies 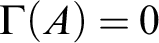 $\Gamma (A)=0$ for each Turing oracle A.
$\Gamma (A)=0$ for each Turing oracle A.
As a dual of the problem 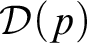 ${\mathcal {D}}(p)$, define
${\mathcal {D}}(p)$, define 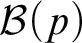 ${\mathcal {B}}(p)$, for
${\mathcal {B}}(p)$, for 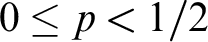 $0 \le p < 1/2$, to be the set of bit sequences y such that
$0 \le p < 1/2$, to be the set of bit sequences y such that 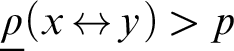 $\underline \rho (x {\,\leftrightarrow\,} y)> p$ for each computable set x. We prove that the Medvedev (and hence Muchnik) complexity of the mass problems
$\underline \rho (x {\,\leftrightarrow\,} y)> p$ for each computable set x. We prove that the Medvedev (and hence Muchnik) complexity of the mass problems 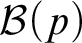 ${\mathcal {B}}(p)$ is the same for all
${\mathcal {B}}(p)$ is the same for all 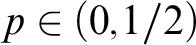 $p \in (0, 1/2)$, by showing that they are Medvedev equivalent to the mass problem of functions bounded by
$p \in (0, 1/2)$, by showing that they are Medvedev equivalent to the mass problem of functions bounded by 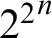 ${2^{2}}^{n}$ that are almost everywhere different from each computable function.
${2^{2}}^{n}$ that are almost everywhere different from each computable function.
Next, together with Joseph Miller, we obtain a proper hierarchy of the mass problems of type 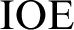 $\text {IOE}$: we show that for any order function g there exists a faster growing order function
$\text {IOE}$: we show that for any order function g there exists a faster growing order function 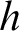 $h $ such that
$h $ such that 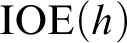 $\text {IOE}(h)$ is strictly above
$\text {IOE}(h)$ is strictly above 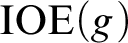 $\text {IOE}(g)$ in the sense of Muchnik reducibility.
$\text {IOE}(g)$ in the sense of Muchnik reducibility.
We study cardinal characteristics in the sense of set theory that are analogous to the highness properties above. For instance, 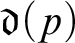 ${\mathfrak {d}} (p)$ is the least size of a set G of bit sequences such that for each bit sequence x there is a bit sequence y in G so that
${\mathfrak {d}} (p)$ is the least size of a set G of bit sequences such that for each bit sequence x there is a bit sequence y in G so that 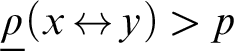 $\underline \rho (x {\,\leftrightarrow\,} y)>p$. We prove within ZFC all the coincidences of cardinal characteristics that are the analogs of the results above.
$\underline \rho (x {\,\leftrightarrow\,} y)>p$. We prove within ZFC all the coincidences of cardinal characteristics that are the analogs of the results above.
MSC classification
Information
- Type
- Article
- Information
- Copyright
- © The Association for Symbolic Logic 2020


