Published online by Cambridge University Press: 17 January 2017
The relative velocities and positions of monodisperse high-inertia particle pairs in isotropic turbulence are studied using direct numerical simulations (DNS), as well as Langevin simulations (LS) based on a probability density function (PDF) kinetic model for pair relative motion. In a prior study (Rani et al., J. Fluid Mech., vol. 756, 2014, pp. 870–902), the authors developed a stochastic theory that involved deriving closures in the limit of high Stokes number for the diffusivity tensor in the PDF equation for monodisperse particle pairs. The diffusivity contained the time integral of the Eulerian two-time correlation of fluid relative velocities seen by pairs that are nearly stationary. The two-time correlation was analytically resolved through the approximation that the temporal change in the fluid relative velocities seen by a pair occurs principally due to the advection of smaller eddies past the pair by large-scale eddies. Accordingly, two diffusivity expressions were obtained based on whether the pair centre of mass remained fixed during flow time scales, or moved in response to integral-scale eddies. In the current study, a quantitative analysis of the (Rani et al. 2014) stochastic theory is performed through a comparison of the pair statistics obtained using LS with those from DNS. LS consist of evolving the Langevin equations for pair separation and relative velocity, which is statistically equivalent to solving the classical Fokker–Planck form of the pair PDF equation. Langevin simulations of particle-pair dispersion were performed using three closure forms of the diffusivity – i.e. the one containing the time integral of the Eulerian two-time correlation of the seen fluid relative velocities and the two analytical diffusivity expressions. In the first closure form, the two-time correlation was computed using DNS of forced isotropic turbulence laden with stationary particles. The two analytical closure forms have the advantage that they can be evaluated using a model for the turbulence energy spectrum that closely matched the DNS spectrum. The three diffusivities are analysed to quantify the effects of the approximations made in deriving them. Pair relative-motion statistics obtained from the three sets of Langevin simulations are compared with the results from the DNS of (moving) particle-laden forced isotropic turbulence for 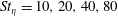 $St_{\unicode[STIX]{x1D702}}=10,20,40,80$ and
$St_{\unicode[STIX]{x1D702}}=10,20,40,80$ and 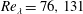 $Re_{\unicode[STIX]{x1D706}}=76,131$. Here,
$Re_{\unicode[STIX]{x1D706}}=76,131$. Here, 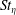 $St_{\unicode[STIX]{x1D702}}$ is the particle Stokes number based on the Kolmogorov time scale and
$St_{\unicode[STIX]{x1D702}}$ is the particle Stokes number based on the Kolmogorov time scale and 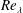 $Re_{\unicode[STIX]{x1D706}}$ is the Taylor micro-scale Reynolds number. Statistics such as the radial distribution function (RDF), the variance and kurtosis of particle-pair relative velocities and the particle collision kernel were computed using both Langevin and DNS runs, and compared. The RDFs from the stochastic runs were in good agreement with those from the DNS. Also computed were the PDFs
$Re_{\unicode[STIX]{x1D706}}$ is the Taylor micro-scale Reynolds number. Statistics such as the radial distribution function (RDF), the variance and kurtosis of particle-pair relative velocities and the particle collision kernel were computed using both Langevin and DNS runs, and compared. The RDFs from the stochastic runs were in good agreement with those from the DNS. Also computed were the PDFs 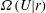 $\unicode[STIX]{x1D6FA}(U|r)$ and
$\unicode[STIX]{x1D6FA}(U|r)$ and 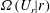 $\unicode[STIX]{x1D6FA}(U_{r}|r)$ of relative velocity
$\unicode[STIX]{x1D6FA}(U_{r}|r)$ of relative velocity 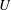 $U$ and of the radial component of relative velocity
$U$ and of the radial component of relative velocity 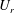 $U_{r}$ respectively, both PDFs conditioned on separation
$U_{r}$ respectively, both PDFs conditioned on separation  $r$. The first closure form, involving the Eulerian two-time correlation of fluid relative velocities, showed the best agreement with the DNS results for the PDFs.
$r$. The first closure form, involving the Eulerian two-time correlation of fluid relative velocities, showed the best agreement with the DNS results for the PDFs.