Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Barkley, D.
2016.
Theoretical perspective on the route to turbulence in a pipe.
Journal of Fluid Mechanics,
Vol. 803,
Issue. ,
Hwang, Yongyun
Willis, Ashley P.
and
Cossu, Carlo
2016.
Invariant solutions of minimal large-scale structures in turbulent channel flow for up to 1000.
Journal of Fluid Mechanics,
Vol. 802,
Issue. ,
Fershtman, A.
Babin, V.
Barnea, D.
and
Shemer, L.
2017.
On shapes and motion of an elongated bubble in downward liquid pipe flow.
Physics of Fluids,
Vol. 29,
Issue. 11,
Ritter, Paul
Zammert, Stefan
Song, Baofang
Eckhardt, Bruno
and
Avila, Marc
2018.
Analysis and modeling of localized invariant solutions in pipe flow.
Physical Review Fluids,
Vol. 3,
Issue. 1,
Priymak, V. G.
2018.
Direct numerical simulation of quasi-equilibrium turbulent puffs in pipe flow.
Physics of Fluids,
Vol. 30,
Issue. 6,
Xu, Duo
and
Avila, Marc
2018.
The effect of pulsation frequency on transition in pulsatile pipe flow.
Journal of Fluid Mechanics,
Vol. 857,
Issue. ,
p.
937.
Rolland, Joran
2018.
Extremely rare collapse and build-up of turbulence in stochastic models of transitional wall flows.
Physical Review E,
Vol. 97,
Issue. 2,
Rinaldi, Enrico
Canton, Jacopo
and
Schlatter, Philipp
2019.
The vanishing of strong turbulent fronts in bent pipes.
Journal of Fluid Mechanics,
Vol. 866,
Issue. ,
p.
487.
Yakhot, Alexander
Feldman, Yuri
Moxey, David
Sherwin, Spencer
and
Karniadakis, George Em
2019.
Turbulence in a Localized Puff in a Pipe.
Flow, Turbulence and Combustion,
Vol. 103,
Issue. 1,
p.
1.
Yakhot, Alexander
Feldman, Yuri
Moxey, David
Sherwin, Spencer
and
Karniadakis, George Em
2019.
Progress in Turbulence VIII.
Vol. 226,
Issue. ,
p.
15.
Winters, K. J.
and
Longmire, E. K.
2019.
PIV-based characterization of puffs in transitional pipe flow.
Experiments in Fluids,
Vol. 60,
Issue. 4,
Picella, Francesco
Bucci, Michele Alessandro
Cherubini, Stefania
and
Robinet, Jean-Christophe
2019.
A synthetic forcing to trigger laminar-turbulent transition in parallel wall bounded flows via receptivity.
Journal of Computational Physics,
Vol. 393,
Issue. ,
p.
92.
Barkley, D.
2019.
Taming turbulent fronts by bending pipes.
Journal of Fluid Mechanics,
Vol. 872,
Issue. ,
p.
1.
Nakayama, Saki
Yamashita, Hiroshi
Yabu, Takuya
Itano, Tomoaki
and
Sugihara-Seki, Masako
2019.
Three regimes of inertial focusing for spherical particles suspended in circular tube flows.
Journal of Fluid Mechanics,
Vol. 871,
Issue. ,
p.
952.
Rigo, Leonardo
Biau, Damien
and
Gloerfelt, Xavier
2020.
The aeroacoustic field produced by a turbulent puff in a duct of square cross section.
Pomyalov, A.
2020.
Dynamics of turbulent plugs in a superfluid
He4
channel counterflow.
Physical Review B,
Vol. 101,
Issue. 13,
Cerbus, R. T.
Sakakibara, J.
Gioia, G.
and
Chakraborty, P.
2020.
The turbulent flow in a slug: a re-examination.
Journal of Fluid Mechanics,
Vol. 883,
Issue. ,
Cerbus, Rory T.
Liu, Chien-chia
Gioia, Gustavo
and
Chakraborty, Pinaki
2020.
Small-scale universality in the spectral structure of transitional pipe flows.
Science Advances,
Vol. 6,
Issue. 4,
Gomé, Sébastien
Tuckerman, Laurette S.
and
Barkley, Dwight
2020.
Statistical transition to turbulence in plane channel flow.
Physical Review Fluids,
Vol. 5,
Issue. 8,
Wang, Xueying
Shih, Hong-Yan
and
Goldenfeld, Nigel
2022.
Stochastic Model for Quasi-One-Dimensional Transitional Turbulence with Streamwise Shear Interactions.
Physical Review Letters,
Vol. 129,
Issue. 3,
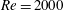 $Re=2000$ and 5500. We here investigate the physical distinction between the fronts of weak and strong slugs both by analysing the turbulent kinetic energy budget and by comparing the downstream front motion to the advection speed of bulk turbulent structures. Our study shows that weak downstream fronts travel slower than turbulent structures in the bulk and correspond to decaying turbulence at the front. At
$Re=2000$ and 5500. We here investigate the physical distinction between the fronts of weak and strong slugs both by analysing the turbulent kinetic energy budget and by comparing the downstream front motion to the advection speed of bulk turbulent structures. Our study shows that weak downstream fronts travel slower than turbulent structures in the bulk and correspond to decaying turbulence at the front. At 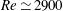 $Re\simeq 2900$ the downstream front speed becomes faster than the advection speed, marking the onset of strong fronts. In contrast to weak fronts, turbulent eddies are generated at strong fronts by feeding on the downstream laminar flow. Our study also suggests that temporal fluctuations of production and dissipation at the downstream laminar–turbulent front drive the dynamical switches between the two types of front observed up to
$Re\simeq 2900$ the downstream front speed becomes faster than the advection speed, marking the onset of strong fronts. In contrast to weak fronts, turbulent eddies are generated at strong fronts by feeding on the downstream laminar flow. Our study also suggests that temporal fluctuations of production and dissipation at the downstream laminar–turbulent front drive the dynamical switches between the two types of front observed up to 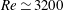 $Re\simeq 3200$.
$Re\simeq 3200$.