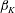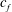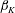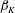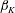1 Introduction
Most investigations of compressible turbulent boundary layers (TBLs) have been performed for zero streamwise pressure gradient (ZPG). In contrast to the ZPG TBL case, however, PG-influenced TBLs are difficult to study systematically since the pressure distribution can arbitrarily change in the streamwise direction, rendering the history of every spatially evolving PG TBL fairly unique (Vinuesa et al. Reference Vinuesa, Hosseini, Hanifi, Henningson and Schlatter2017). The dynamic properties of the TBL are strongly influenced by this history even in the ZPG case (Perry, Marusic & Jones Reference Perry, Marusic and Jones2002) and thus strongly depend upon the specific distribution of the streamwise PG. In the incompressible regime, a fundamental part of understanding PG effects is therefore gained from self-similar PG TBLs, meaning that all or at least the most important terms of the governing equations have the same proportionality in their streamwise evolution. Since Reynolds-number effects are largely excluded and history effects clearly and reproducibly defined due to the equilibrium character of the resulting flow, PG effects can be isolated and generalized conclusions drawn, see Stratford (Reference Stratford1959), Skåre & Krogstad (Reference Skåre and Krogstad1994), Skote, Henningson & Henkes (Reference Skote, Henningson and Henkes1998), Lee & Sung (Reference Lee and Sung2008), Kitsios et al. (Reference Kitsios, Atkinson, Sillero, Borrell, Gungor, Jiménez and Soria2016), Bobke et al. (Reference Bobke, Vinuesa, Örlü and Schlatter2017), Kitsios et al. (Reference Kitsios, Sekimoto, Atkinson, Sillero, Borrell, Gungor, Jiménez and Soria2017) and Lee (Reference Lee2017).
In many aspects, the understanding of PG effects is more intricate in the compressible regime, even without taking the aspect of self-similarity into account. PGs are additionally linked for instance to Mach number and thus wall-temperature/heat-flux variations in the streamwise direction. Supersonic boundary layers possess both a subsonic near-wall region and a supersonic outer part, and the overall effects of PGs are not readily predictable since the thickening of the boundary layer is the result of two opposing effects. While streamtubes tend to diverge for APGs in the subsonic near-wall region, they tend to converge in the supersonic outer part of the boundary layer (Smits & Dussauge Reference Smits and Dussauge2006). Mainly caused by its spatially parabolic character and the presence of strong density variations in the wall-normal direction, the response of the supersonic PG TBL also highly depends on the way the PG is imposed. Different set-ups invoke additional phenomena strongly superimposing on the effect of ‘pure’ PGs. For compression ramps, for instance, the boundary layer is mainly affected by a (slightly oscillating) shock and a small region of separated flow in the corner, both significantly amplifying the level of turbulent fluctuations, see Ardonceau (Reference Ardonceau1984), Dussauge & Gaviglio (Reference Dussauge and Gaviglio1987), Smits & Muck (Reference Smits and Muck1987), Selig et al. (Reference Selig, Andreopoulos, Muck, Dussauge and Smits1989), Adams (Reference Adams2000), Wu & Martin (Reference Wu and Martin2007), Fang et al. (Reference Fang, Yao, Zheltovodov, Li and Lu2015) and Sun, Hu & Sandham (Reference Sun, Hu and Sandham2017), among others. Boundary layers over convex/concave curved surfaces, on the other hand, are additionally influenced by streamline curvature, wall-normal PGs, bulk dilatation and Görtler vortices, see Bradshaw (Reference Bradshaw1973, Reference Bradshaw1974), Jayaram, Taylor & Smits (Reference Jayaram, Taylor and Smits1987), Donovan, Spina & Smits (Reference Donovan, Spina and Smits1994), Bowersox & Buter (Reference Bowersox and Buter1996), Arnette, Samimy & Elliott (Reference Arnette, Samimy and Elliott1998), Luker et al. (Reference Luker, Bowersox, Rodney and Buter2000), Tichenor, Humble & Bowersox (Reference Tichenor, Humble and Bowersox2013) and Wang, Wang & Zhao (Reference Wang, Wang and Zhao2016a ), for instance.
As a consequence, nearly everything known about pure PG effects on compressible TBLs has been gained from investigations of reflected-wave set-ups where the PG is imposed by a smoothly shaped body placed above a flat plate. The principal strain rate and the bulk dilatation are only slightly changed in the near-wall region along the streamwise direction in such flows (Wang, Wang & Zhao Reference Wang, Wang and Zhao2016b ). Hence, the reflected-wave set-up is the only case which really allows the isolation and thus a meaningful discussion of pure PG effects in the compressible regime. Although the gross effects of PGs on compressible TBLs are understood or at least well described, a lot of fundamental questions remain.
One of the main problem seems to be that only a few experimental realizations (and no DNS data at all) of the reflected-wave set-up are available in the literature, and thus data being accurate or complete enough to verify theoretical results are lacking, see, e.g. Fernholz, Finley & Mikulla (Reference Fernholz, Finley and Mikulla1981), Fernholz et al. (Reference Fernholz, Dussauge, Finlay, Smits and Reshotko1989), Fernando & Smits (Reference Fernando and Smits1990), Smith & Smits (Reference Smith and Smits1997), Franko & Lele (Reference Franko and Lele2014), Wang et al. (Reference Wang, Wang and Zhao2016b ) and Wang, Wang & Zhao (Reference Wang, Wang and Zhao2017). Compressibility transformations such as Morkovin’s scaling or van Driest’s transformation are derived under somewhat restrictive conditions which are assumed to be only approximately valid for the special case of the compressible ZPG TBL. Both, however, represent the basis for the description and thus our understanding of compressible TBLs, since they directly connect the compressible and incompressible regimes. This does not imply that they do not hold for PG cases, but due to the scarcity of data, their validity is not proven. In fact, experimental data transformed via van Driest’s transformation show good agreement with incompressible data correlations for various wall-heating conditions and modest PGs. However, since the exact incompressible counterparts of the compressible problems are generally not known and often not even realizable for incompressible flows, this agreement is primarily qualitative (Cebeci & Bradshaw Reference Cebeci and Bradshaw1984). Furthermore, also the influence of PGs on the turbulent Prandtl number, the recovery factor and thus on the adiabatic wall temperature is unknown. All are of central importance for the derivation of turbulence models, as their success largely depends on the possibly physics-based modelling/universality of these values.
When considering the importance of compressible PG flows for e.g. commercial aviation or gas turbines, it would be highly desirable to extend the knowledge about pure PG effects on compressible TBLs by using DNS. These studies should be done with the same systematic approach as has been used for the incompressible regime so far by investigating self-similar PG TBLs. It is surprising, however, that virtually nothing is known from the analytical or numerical/experimental perspective about the canonical case of the compressible self-similar PG TBLs at all, despite the fact that its understanding/description should actually be the first step to understand PG effects in general in the compressible regime. It is not even clear to which degree any kind of self-similarity can be obtained in the turbulent compressible regime, if at all. It can certainly be expected that the compressible turbulent boundary-layer equations allow self-similar solutions due to the close relationship between the Favre-averaged and the incompressible Reynolds-averaged representations which are used as a starting point for self-similarity investigations. However, the concept of compressible self-similarity must compensate both Reynolds-number and compressibility effects caused by Mach-number variations in the streamwise direction, and its existence is not readily apparent.
1.1 Objectives of this study
It is the primary goal of this study to systematically investigate the effects of pure PGs on compressible TBLs by considering locally self-similar compressible PG TBLs via DNS. The equilibrium character of this canonical case should allow generalizable insight into the isolated effects of pure PGs on compressible turbulence and thus a well-described starting point for related investigations. Furthermore, it should allow for a direct comparison between compressible and incompressible cases (which are expected to be mutual counterparts) and thus the evaluation of compressibility transformations and Morkovin’s hypothesis (Morkovin Reference Morkovin and Favre1961), which have only been proven for ZPG TBLs so far.
The achievement of approximate self-similarity, however, cannot be assessed for flow data without understanding the theoretical conditions for self-similarity. Critical assumptions which have to be made for a compressible self-similarity analysis, however, cannot be verified without having data available. To this end, both a theoretically derived self-similarity analysis and results of carefully conducted DNS of self-similar compressible PG TBL are presented for the first time. Since only few investigations are available in the literature providing any detailed reference data of compressible PG TBLs, reliable DNS results are sought in general even without taking the aspect of self-similarity into account. The present investigations are therefore subdivided into two parts, the present first part which is mainly focused on the DNS results, and a second part which is mainly focused on the derivation/validation of compressible self-similarity, see Gibis et al. (Reference Gibis, Wenzel, Kloker and Rist2019).
The present study is structured as follows: in order to allow for a clear understanding of the present DNS study, both the numerical methodology and the numerical set-ups employed are summarized in § 2. The following results section is split into two parts. While the first part (§ 3) mainly characterizes the spatial evolution of the resulting compressible flow fields, the validity of compressibility transformations applied to local mean-flow-field profiles is assessed in the second part (§ 4). Concluding remarks are given in § 5.
2 Methodology and numerical set-up
First the modelling of the free-stream pressure distributions is presented, followed by a summary of the simulation parameters. To enable a clear interpretation of the results in the following, effects which are mainly caused by density variations due to a fixed non-small Mach number are referred to as compressibility effects. Shock-wave phenomena (by APGs), which may possibly occur, are referred to as supersonic effects. Quantities with an overbar represent quantities averaged in both the spanwise direction and time. The subscripts ‘
![]() $w$
’ and ‘
$w$
’ and ‘
![]() $e$
’ refer to wall and free-stream quantities, respectively, see Wenzel et al. (Reference Wenzel, Selent, Kloker and Rist2018b
) for details.
$e$
’ refer to wall and free-stream quantities, respectively, see Wenzel et al. (Reference Wenzel, Selent, Kloker and Rist2018b
) for details.
2.1 Methodology of the present study
DNS results are computed for the canonical case of the self-similar (equilibrium) compressible PG TBL both for moderate APG and FPG cases. Therefore, all cases should be characterized by long distances of a constant kinematic Rotta–Clauser parameter
![]() $\unicode[STIX]{x1D6FD}_{K}=(\unicode[STIX]{x1D6FF}_{K}^{\ast }/\overline{\unicode[STIX]{x1D70F}}_{w})(\text{d}p_{e}/\text{d}x)$
, where
$\unicode[STIX]{x1D6FD}_{K}=(\unicode[STIX]{x1D6FF}_{K}^{\ast }/\overline{\unicode[STIX]{x1D70F}}_{w})(\text{d}p_{e}/\text{d}x)$
, where
![]() $\unicode[STIX]{x1D6FF}_{K}^{\ast }$
is the kinematic displacement thickness (see § 3.2.1),
$\unicode[STIX]{x1D6FF}_{K}^{\ast }$
is the kinematic displacement thickness (see § 3.2.1),
![]() $\overline{\unicode[STIX]{x1D70F}}_{w}$
the mean wall shear stress and
$\overline{\unicode[STIX]{x1D70F}}_{w}$
the mean wall shear stress and
![]() $\text{d}p_{e}/\text{d}x$
the pressure gradient in streamwise direction evaluated at the edge of the boundary layer. It was found that those regions still yield the state of approximate streamwise self-similarity in the compressible regime, see § 4.1.1 and Gibis et al. (Reference Gibis, Wenzel, Kloker and Rist2019) for a detailed discussion. The use of both sub- and supersonic inflow Mach numbers should further allow for a meaningful comparison between the incompressible/subsonic and the compressible/supersonic regimes. As summarized in table 1, three nearly incompressible APG cases are investigated with inflow Mach numbers of
$\text{d}p_{e}/\text{d}x$
the pressure gradient in streamwise direction evaluated at the edge of the boundary layer. It was found that those regions still yield the state of approximate streamwise self-similarity in the compressible regime, see § 4.1.1 and Gibis et al. (Reference Gibis, Wenzel, Kloker and Rist2019) for a detailed discussion. The use of both sub- and supersonic inflow Mach numbers should further allow for a meaningful comparison between the incompressible/subsonic and the compressible/supersonic regimes. As summarized in table 1, three nearly incompressible APG cases are investigated with inflow Mach numbers of
![]() $M_{\infty ,0}=0.5$
, yielding Rotta–Clauser parameters of
$M_{\infty ,0}=0.5$
, yielding Rotta–Clauser parameters of
![]() $\unicode[STIX]{x1D6FD}_{K}=0.19$
, 0.58 and 1.05. The subscript ‘
$\unicode[STIX]{x1D6FD}_{K}=0.19$
, 0.58 and 1.05. The subscript ‘
![]() $\infty$
’ represents far-field values, the subscript ‘0’ values evaluated at the inflow of the domain. For the compressible, supersonic regime four APG cases and one FPG case are investigated with inflow Mach numbers of
$\infty$
’ represents far-field values, the subscript ‘0’ values evaluated at the inflow of the domain. For the compressible, supersonic regime four APG cases and one FPG case are investigated with inflow Mach numbers of
![]() $M_{\infty ,0}=2.0$
, yielding
$M_{\infty ,0}=2.0$
, yielding
![]() $\unicode[STIX]{x1D6FD}_{K}=0.15$
, 0.42, 0.55 and 0.69 for the APG and
$\unicode[STIX]{x1D6FD}_{K}=0.15$
, 0.42, 0.55 and 0.69 for the APG and
![]() $\unicode[STIX]{x1D6FD}_{K}=-0.18$
for the FPG case. Additionally, ZPG cases are computed for both inflow Mach numbers with the same set-up to provide reference data for all PG cases. In order to benefit from the verified reliability of the ZPG set-ups, see Wenzel et al. (Reference Wenzel, Selent, Kloker and Rist2018b
), the same inflow Reynolds number of about
$\unicode[STIX]{x1D6FD}_{K}=-0.18$
for the FPG case. Additionally, ZPG cases are computed for both inflow Mach numbers with the same set-up to provide reference data for all PG cases. In order to benefit from the verified reliability of the ZPG set-ups, see Wenzel et al. (Reference Wenzel, Selent, Kloker and Rist2018b
), the same inflow Reynolds number of about
![]() $Re_{\unicode[STIX]{x1D703}}\approx 300$
is chosen for all cases.
$Re_{\unicode[STIX]{x1D703}}\approx 300$
is chosen for all cases.
2.2 Numerical method
All computations are performed with the compressible high-order in-house DNS code
![]() $NS3D$
; fundamentals are described in Babucke (Reference Babucke2009), Linn & Kloker (Reference Linn, Kloker and Gülhan2008, Reference Linn and Kloker2011), Keller & Kloker (Reference Keller and Kloker2014, Reference Keller and Kloker2016) and Wenzel et al. (Reference Wenzel, Peter, Selent, Weinschenk, Rist, Kloker and Nagel2018a
). With the velocity vector
$NS3D$
; fundamentals are described in Babucke (Reference Babucke2009), Linn & Kloker (Reference Linn, Kloker and Gülhan2008, Reference Linn and Kloker2011), Keller & Kloker (Reference Keller and Kloker2014, Reference Keller and Kloker2016) and Wenzel et al. (Reference Wenzel, Peter, Selent, Weinschenk, Rist, Kloker and Nagel2018a
). With the velocity vector
![]() $\boldsymbol{u}=[u,v,w]^{T}$
with components in the streamwise, wall-normal and spanwise directions
$\boldsymbol{u}=[u,v,w]^{T}$
with components in the streamwise, wall-normal and spanwise directions
![]() $x$
,
$x$
,
![]() $y$
and
$y$
and
![]() $z$
, the dimensionless solution vector is
$z$
, the dimensionless solution vector is
![]() $\boldsymbol{Q}=[\unicode[STIX]{x1D70C},\unicode[STIX]{x1D70C}u,\unicode[STIX]{x1D70C}v,\unicode[STIX]{x1D70C}w,E]^{T}$
, where
$\boldsymbol{Q}=[\unicode[STIX]{x1D70C},\unicode[STIX]{x1D70C}u,\unicode[STIX]{x1D70C}v,\unicode[STIX]{x1D70C}w,E]^{T}$
, where
![]() $\unicode[STIX]{x1D70C}$
and
$\unicode[STIX]{x1D70C}$
and
![]() $E$
are the density and the total energy, respectively. Velocities and length scales are normalized by the streamwise reference velocity
$E$
are the density and the total energy, respectively. Velocities and length scales are normalized by the streamwise reference velocity
![]() $u_{\infty }$
and the reference length
$u_{\infty }$
and the reference length
![]() $L=\unicode[STIX]{x1D6FF}_{99,0}$
, respectively, where
$L=\unicode[STIX]{x1D6FF}_{99,0}$
, respectively, where
![]() $\unicode[STIX]{x1D6FF}_{99,0}$
is the boundary-layer thickness at the inflow of the domain. Temperature or density are normalized by the reference temperature
$\unicode[STIX]{x1D6FF}_{99,0}$
is the boundary-layer thickness at the inflow of the domain. Temperature or density are normalized by the reference temperature
![]() $T_{\infty }$
and the reference density
$T_{\infty }$
and the reference density
![]() $\unicode[STIX]{x1D70C}_{\infty }$
; similarly for the thermal conductivity
$\unicode[STIX]{x1D70C}_{\infty }$
; similarly for the thermal conductivity
![]() $\unicode[STIX]{x1D717}$
and the dynamic viscosity
$\unicode[STIX]{x1D717}$
and the dynamic viscosity
![]() $\unicode[STIX]{x1D707}$
. Specific heats and the pressure
$\unicode[STIX]{x1D707}$
. Specific heats and the pressure
![]() $p$
are non-dimensionalized by
$p$
are non-dimensionalized by
![]() $u_{\infty }^{2}/T_{\infty }$
and
$u_{\infty }^{2}/T_{\infty }$
and
![]() $\unicode[STIX]{x1D70C}_{\infty }u_{\infty }^{2}$
, respectively. The ratio
$\unicode[STIX]{x1D70C}_{\infty }u_{\infty }^{2}$
, respectively. The ratio
![]() $\unicode[STIX]{x1D6FE}=c_{p}/c_{v}=1.4$
and the Prandtl number
$\unicode[STIX]{x1D6FE}=c_{p}/c_{v}=1.4$
and the Prandtl number
![]() $Pr=0.71$
are assumed constant. The temperature dependence of the viscosity is modelled by Sutherland’s law and the linear law below the Sutherland temperature. The equations are solved on a block-structured Cartesian grid spanning a rectangular integration domain.
$Pr=0.71$
are assumed constant. The temperature dependence of the viscosity is modelled by Sutherland’s law and the linear law below the Sutherland temperature. The equations are solved on a block-structured Cartesian grid spanning a rectangular integration domain.
Either sixth-order subdomain-compact finite differences (FDs) or eighth-order explicit FDs are used for the three spatial directions, see Keller & Kloker (Reference Keller and Kloker2013) or Babucke (Reference Babucke2009), Keller (Reference Keller2016) and Dörr (Reference Dörr2018), respectively; compact FDs are more stable for the supersonic cases. The classical explicit fourth-order Runge–Kutta scheme is used for time integration, coupled with alternating forward- and backward-biased FDs for the convective first derivatives, see Kloker (Reference Kloker1997) and Babucke (Reference Babucke2009).
2.3 Numerical set-up and boundary conditions
The numerical set-ups for the sub- and supersonic cases differ somewhat. For instance, the thickening of the boundary layer is less for supersonic than for subsonic APG cases, which effectively allows longer simulation domains for the same domain width in the supersonic case. Caused by the opposing effect of APGs on the effective grid resolution – increasing in the subsonic and decreasing in the supersonic case in terms of wall units for a fixed grid step – also the numerical grid has to be designed independently for both regimes. Furthermore, the pressure distribution noticeably varies across the far field – initially it is determined for the edge of the boundary layer but prescribed at the upper boundary of the simulation domain. The height of the domain thus has to be restricted to a minimum to minimize the distortion of the pressure distribution reaching the boundary layer. The set-ups for the sub- and supersonic cases are described below independently.
2.3.1 Subsonic cases

Figure 1. Simulation domain for present subsonic PG simulations. The yellow coloured regions represent sponge zones, blue shaded regions between
![]() $x_{end}$
and
$x_{end}$
and
![]() $x_{max}$
regions where grid stretching is applied in the streamwise direction to make spatial filtering effective. The red-bordered zone represents the main region of the simulations. (a) Simplified simulation domain for the calculation of physical mean values for sponge-zone application. (b) Simulation domain for the final calculation. The yellow coloured sponge regions force the unsteady flow to the previously calculated mean-flow values, which are set as new base-flow values.
$x_{max}$
regions where grid stretching is applied in the streamwise direction to make spatial filtering effective. The red-bordered zone represents the main region of the simulations. (a) Simplified simulation domain for the calculation of physical mean values for sponge-zone application. (b) Simulation domain for the final calculation. The yellow coloured sponge regions force the unsteady flow to the previously calculated mean-flow values, which are set as new base-flow values.
A sketch of the subsonic simulation domain is presented in figure 1. The main region of the computational box (red framed in figure 1
a,b) is designed with a height of at least three boundary-layer thicknesses
![]() $\unicode[STIX]{x1D6FF}_{99,end}$
in the wall-normal
$\unicode[STIX]{x1D6FF}_{99,end}$
in the wall-normal
![]() $y$
-direction, measured at the end of the main region
$y$
-direction, measured at the end of the main region
![]() $x_{end}$
for the most restricting
$x_{end}$
for the most restricting
![]() $\unicode[STIX]{x1D6FD}_{K}=1.05$
case. The width is approximately
$\unicode[STIX]{x1D6FD}_{K}=1.05$
case. The width is approximately
![]() $\unicode[STIX]{x03C0}\,\unicode[STIX]{x1D6FF}_{99,end}$
in the spanwise
$\unicode[STIX]{x03C0}\,\unicode[STIX]{x1D6FF}_{99,end}$
in the spanwise
![]() $z$
-direction. Measured in boundary-layer thicknesses at the inflow of the simulation domain (
$z$
-direction. Measured in boundary-layer thicknesses at the inflow of the simulation domain (
![]() $Re_{\unicode[STIX]{x1D703}}\approx 300$
), the main region of the computational box has a dimension of
$Re_{\unicode[STIX]{x1D703}}\approx 300$
), the main region of the computational box has a dimension of
![]() $340\,\unicode[STIX]{x1D6FF}_{99,0}\times 34\,\unicode[STIX]{x1D6FF}_{99,0}\times 12\unicode[STIX]{x03C0}\,\unicode[STIX]{x1D6FF}_{99,0}$
, respectively. The length of the PG set-up in the streamwise
$340\,\unicode[STIX]{x1D6FF}_{99,0}\times 34\,\unicode[STIX]{x1D6FF}_{99,0}\times 12\unicode[STIX]{x03C0}\,\unicode[STIX]{x1D6FF}_{99,0}$
, respectively. The length of the PG set-up in the streamwise
![]() $x$
-direction thus corresponds to 73 % of the ZPG case discussed in Wenzel et al. (Reference Wenzel, Selent, Kloker and Rist2018b
) whereas the width corresponds to 150 %.
$x$
-direction thus corresponds to 73 % of the ZPG case discussed in Wenzel et al. (Reference Wenzel, Selent, Kloker and Rist2018b
) whereas the width corresponds to 150 %.
At the solid wall, the flow field is treated as fully adiabatic at every time instance with
![]() $(\text{d}T/\text{d}y)_{w}=0$
, which suppresses any heat exchange between the wall and fluid; the pressure at the wall is calculated by
$(\text{d}T/\text{d}y)_{w}=0$
, which suppresses any heat exchange between the wall and fluid; the pressure at the wall is calculated by
![]() $(\text{d}p/\text{d}y)_{w}=0$
. For the velocity components, the no-slip impermeable wall BC is applied. At the outflow, the time derivative, respectively the complete space operator, is extrapolated with
$(\text{d}p/\text{d}y)_{w}=0$
. For the velocity components, the no-slip impermeable wall BC is applied. At the outflow, the time derivative, respectively the complete space operator, is extrapolated with
![]() $\unicode[STIX]{x2202}\boldsymbol{Q}/\unicode[STIX]{x2202}t|_{N}=\unicode[STIX]{x2202}\boldsymbol{Q}/\unicode[STIX]{x2202}t|_{N-1}$
corresponding to a first-order extrapolation. At the top of the domain,
$\unicode[STIX]{x2202}\boldsymbol{Q}/\unicode[STIX]{x2202}t|_{N}=\unicode[STIX]{x2202}\boldsymbol{Q}/\unicode[STIX]{x2202}t|_{N-1}$
corresponding to a first-order extrapolation. At the top of the domain,
![]() $p$
,
$p$
,
![]() $T$
and thus also
$T$
and thus also
![]() $\unicode[STIX]{x1D70C}$
are kept constant. The velocity components
$\unicode[STIX]{x1D70C}$
are kept constant. The velocity components
![]() $u$
and
$u$
and
![]() $w$
are specified by
$w$
are specified by
![]() $\text{d}/\text{d}y=0$
; the wall-normal velocity component
$\text{d}/\text{d}y=0$
; the wall-normal velocity component
![]() $v$
is calculated from the continuity equation under the assumption of
$v$
is calculated from the continuity equation under the assumption of
![]() $\text{d}\unicode[STIX]{x1D70C}/\text{d}y=0$
such that
$\text{d}\unicode[STIX]{x1D70C}/\text{d}y=0$
such that
![]() $\text{d}v/\text{d}y=-1/\unicode[STIX]{x1D70C}(\text{d}(\unicode[STIX]{x1D70C}u)/\text{d}x+\text{d}(\unicode[STIX]{x1D70C}w)/\text{d}z)$
. Caused by the non-characteristic behaviour of this BC, the additional application of numerical grid stretching and filtering and/or additional sponge zones is necessary if sound-wave reflection should be suppressed. At the inflow, a digital-filtering synthetic-eddy-method (SEM) approach is used to generate an unsteady, turbulent inflow condition, see Wenzel et al. (Reference Wenzel, Selent, Kloker and Rist2018b
) or Wenzel (Reference Wenzel2019). The spanwise direction is treated as periodic.
$\text{d}v/\text{d}y=-1/\unicode[STIX]{x1D70C}(\text{d}(\unicode[STIX]{x1D70C}u)/\text{d}x+\text{d}(\unicode[STIX]{x1D70C}w)/\text{d}z)$
. Caused by the non-characteristic behaviour of this BC, the additional application of numerical grid stretching and filtering and/or additional sponge zones is necessary if sound-wave reflection should be suppressed. At the inflow, a digital-filtering synthetic-eddy-method (SEM) approach is used to generate an unsteady, turbulent inflow condition, see Wenzel et al. (Reference Wenzel, Selent, Kloker and Rist2018b
) or Wenzel (Reference Wenzel2019). The spanwise direction is treated as periodic.
In order to allow a smooth transition process with a defined state from the pseudo-physical to a fully developed turbulent state, a ZPG region with a spatial extent of
![]() $30\unicode[STIX]{x1D6FF}_{99,0}$
is applied at the inflow of the domain before the PG is forced, see § 2.4. The induction distance for reaching fully developed turbulence is therefore the same as for the ZPG case at
$30\unicode[STIX]{x1D6FF}_{99,0}$
is applied at the inflow of the domain before the PG is forced, see § 2.4. The induction distance for reaching fully developed turbulence is therefore the same as for the ZPG case at
![]() $M_{\infty }=0.5$
(
$M_{\infty }=0.5$
(
![]() $\unicode[STIX]{x0394}x_{ind}/\unicode[STIX]{x1D6FF}_{99,0}\approx 28$
, see table 2 and Wenzel et al. (Reference Wenzel, Selent, Kloker and Rist2018b
)), and similar for all PG distributions. A sponge region is applied outside the boundary layer at the inflow to prevent the included far-field flow from being unduly distorted by the transient process, see Schmidt (Reference Schmidt2014), Kurz & Kloker (Reference Kurz and Kloker2014) and Wenzel (Reference Wenzel2019). The sponge zone fixes the constant pressure region in the far field through the inflow region, which otherwise is strongly influenced by the retroactive effect of the PG applied further downstream. Only in the streamwise direction, geometrical grid stretching is applied to the numerical grid in the outflow region, see Wenzel (Reference Wenzel2019).
$\unicode[STIX]{x0394}x_{ind}/\unicode[STIX]{x1D6FF}_{99,0}\approx 28$
, see table 2 and Wenzel et al. (Reference Wenzel, Selent, Kloker and Rist2018b
)), and similar for all PG distributions. A sponge region is applied outside the boundary layer at the inflow to prevent the included far-field flow from being unduly distorted by the transient process, see Schmidt (Reference Schmidt2014), Kurz & Kloker (Reference Kurz and Kloker2014) and Wenzel (Reference Wenzel2019). The sponge zone fixes the constant pressure region in the far field through the inflow region, which otherwise is strongly influenced by the retroactive effect of the PG applied further downstream. Only in the streamwise direction, geometrical grid stretching is applied to the numerical grid in the outflow region, see Wenzel (Reference Wenzel2019).
Due to the limited height of the simulation domain, the realizable total grid cell increase and thus the effect of the numerical filter is limited in the wall-normal direction in the far field of the domain. Possible reflections occurring at the far-field boundary are therefore suppressed by the application of additional sponge zones. These are to damp the unsteady flow to a prescribed mean flow not known a priori. To generate this mean flow, a precursor simulation is computed on a preliminary set-up for all PG cases, see figure 1(a). Weak reflections occurring at the far-field boundary are not treated by this set-up since they have been found to average out in the temporal mean. The accuracy of the resulting flow field has been verified by a comparison with the ZPG case given in Wenzel et al. (Reference Wenzel, Selent, Kloker and Rist2018b ). At the outlet of the simulation domain, a small sponge zone is applied to avoid a temporal drift of the outlet pressure. This sponge damps the flow field to a spatially undeveloped reference solution defined a priori. Hence, to minimize the distortion of the flow field, its effectiveness is reduced to 30 % of the inflow sponge. The resulting mean flow is used as a new base flow for the final set-up in a second step, which allows the application of additional sponge zones at the far-field boundary and the outflow region, both with the same effectiveness as the inflow sponge. A sketch of the final set-up is given in figure 1(b).
2.3.2 Supersonic cases
A sketch of the supersonic simulation domain is depicted in figure 2. Caused by the spatially hyperbolic behaviour of the supersonic flow, the pressure information is only allowed to move along the angle of the flow’s local characteristics. Thus, prescribed by the far-field BC at the top of the domain, the information of the particular PG is diagonally transmitted as Mach waves (shock waves if the PG is too strong) down to the plate (black solid lines in figure 2) where they are reflected (black dashed lines). The final pressure field results from the superposition of the prescribed, incoming and the reflected, outgoing waves. Both yield a complex flow field with lines of constant pressure being almost perpendicular to the wall for regions of fully established wave systems (cyan coloured solid lines). The induction length (inflow region in figure 2) therefore depends on the Mach number, the length of the ZPG inflow region and the height of the simulation domain. Hence, it is fixed by the particular numerical set-up.

Figure 2. Simulation domain for present supersonic PG simulations. The yellow and blue shaded regions represent sponged and grid-stretched zones, respectively. The main region of the simulation is red bordered. Pressure information introduced at the far field moves diagonally to the wall (black solid lines) and is reflected (black dashed lines). The final pressure field is depicted by cyan coloured solid lines.
For the present simulations, the main region of the computational box (red framed in figure 2) is designed with a height of at least three boundary-layer thicknesses
![]() $\unicode[STIX]{x1D6FF}_{99,end}$
in the wall-normal
$\unicode[STIX]{x1D6FF}_{99,end}$
in the wall-normal
![]() $y$
-direction and a width of approximately
$y$
-direction and a width of approximately
![]() $\unicode[STIX]{x03C0}\,\unicode[STIX]{x1D6FF}_{99,end}$
in the spanwise
$\unicode[STIX]{x03C0}\,\unicode[STIX]{x1D6FF}_{99,end}$
in the spanwise
![]() $z$
-direction for the most restricting
$z$
-direction for the most restricting
![]() $\unicode[STIX]{x1D6FD}_{K}=0.69$
case. Measured in boundary-layer thicknesses at the inflow of the simulation domain (
$\unicode[STIX]{x1D6FD}_{K}=0.69$
case. Measured in boundary-layer thicknesses at the inflow of the simulation domain (
![]() $Re_{\unicode[STIX]{x1D703}}\approx 300$
), the main region of the computational box has a dimension of
$Re_{\unicode[STIX]{x1D703}}\approx 300$
), the main region of the computational box has a dimension of
![]() $500\,\unicode[STIX]{x1D6FF}_{99,0}\times 34\,\unicode[STIX]{x1D6FF}_{99,0}\times 12\unicode[STIX]{x03C0}\,\unicode[STIX]{x1D6FF}_{99,0}$
, respectively. The length of the PG set-up in the streamwise
$500\,\unicode[STIX]{x1D6FF}_{99,0}\times 34\,\unicode[STIX]{x1D6FF}_{99,0}\times 12\unicode[STIX]{x03C0}\,\unicode[STIX]{x1D6FF}_{99,0}$
, respectively. The length of the PG set-up in the streamwise
![]() $x$
-direction thus corresponds to 107 % of the ZPG cases discussed in Wenzel et al. (Reference Wenzel, Selent, Kloker and Rist2018b
) and 147 % of the previously presented subsonic PG cases.
$x$
-direction thus corresponds to 107 % of the ZPG cases discussed in Wenzel et al. (Reference Wenzel, Selent, Kloker and Rist2018b
) and 147 % of the previously presented subsonic PG cases.
The outflow is parabolized by neglecting the second
![]() $x$
-derivatives; biased difference stencils are used for the first
$x$
-derivatives; biased difference stencils are used for the first
![]() $x$
-derivatives. At the top of the simulation domain, a subsonic characteristic outflow BC is applied according to Poinsot & Lele (Reference Poinsot and Lele1991) (see also Babucke (Reference Babucke2009), Franko & Lele (Reference Franko and Lele2014)). Its implementation allows upward travelling (outgoing) disturbances to leave the integration domain, whereas downward travelling (incoming) disturbances are set to zero in order to avoid reflections. This BC, in fact, allows the mean pressure to adapt at the upper boundary, see below. A detailed justification and discussion of its use is given in Wenzel (Reference Wenzel2019).
$x$
-derivatives. At the top of the simulation domain, a subsonic characteristic outflow BC is applied according to Poinsot & Lele (Reference Poinsot and Lele1991) (see also Babucke (Reference Babucke2009), Franko & Lele (Reference Franko and Lele2014)). Its implementation allows upward travelling (outgoing) disturbances to leave the integration domain, whereas downward travelling (incoming) disturbances are set to zero in order to avoid reflections. This BC, in fact, allows the mean pressure to adapt at the upper boundary, see below. A detailed justification and discussion of its use is given in Wenzel (Reference Wenzel2019).
Following the same ideas as for the subsonic set-ups, a ZPG region with a spatial extent of
![]() $80\,\unicode[STIX]{x1D6FF}_{99,0}$
is applied at the inflow of the domain before the PG is forced (see next section for details). The induction distance until turbulence is fully developed is therefore the same as for the ZPG case at
$80\,\unicode[STIX]{x1D6FF}_{99,0}$
is applied at the inflow of the domain before the PG is forced (see next section for details). The induction distance until turbulence is fully developed is therefore the same as for the ZPG case at
![]() $M_{\infty }=2.0$
(
$M_{\infty }=2.0$
(
![]() $\unicode[STIX]{x0394}x_{ind}/\unicode[STIX]{x1D6FF}_{99,0}\approx 60$
, see table 2 and Wenzel et al. (Reference Wenzel, Selent, Kloker and Rist2018b
)), and identical for all different PG distributions. As for the subsonic cases, an identically dimensioned sponge region is applied at the inflow of the domain to absorb the shock system which is caused by the transient process of the inflow BC. It is noted that the prescribed wall-normal velocity component
$\unicode[STIX]{x0394}x_{ind}/\unicode[STIX]{x1D6FF}_{99,0}\approx 60$
, see table 2 and Wenzel et al. (Reference Wenzel, Selent, Kloker and Rist2018b
)), and identical for all different PG distributions. As for the subsonic cases, an identically dimensioned sponge region is applied at the inflow of the domain to absorb the shock system which is caused by the transient process of the inflow BC. It is noted that the prescribed wall-normal velocity component
![]() $v$
, to which the flow field is damped down in the sponge region, has to closely match the one generated by the boundary layer itself. A mismatch of both velocities causes a discontinuity (exemplarily given in figure 2 as dotted lines at the inflow), which is reflected by the upper boundary and thus affects the flow field in the whole simulation domain. A detailed derivation of an analytical velocity adaption procedure can be found in Gibis (Reference Gibis2018). The outflow region of the simulation domain is only slightly stretched and filtered to avoid reflections from the outflow BC in the subsonic near-wall regions of the boundary layer. It was found that no additional outflow sponge region is required.
$v$
, to which the flow field is damped down in the sponge region, has to closely match the one generated by the boundary layer itself. A mismatch of both velocities causes a discontinuity (exemplarily given in figure 2 as dotted lines at the inflow), which is reflected by the upper boundary and thus affects the flow field in the whole simulation domain. A detailed derivation of an analytical velocity adaption procedure can be found in Gibis (Reference Gibis2018). The outflow region of the simulation domain is only slightly stretched and filtered to avoid reflections from the outflow BC in the subsonic near-wall regions of the boundary layer. It was found that no additional outflow sponge region is required.
2.4 Modelling of the free-stream pressure distribution
In the incompressible regime, the self-similar state of the PG TBL is usually predicted by evaluation of the non-dimensional Rotta–Clauser parameter
![]() $\unicode[STIX]{x1D6FD}_{K}=(\unicode[STIX]{x1D6FF}_{K}^{\ast }/\overline{\unicode[STIX]{x1D70F}}_{w})\,(\text{d}p_{e}/\text{d}x)$
, which must be constant for all streamwise positions. Following the idea of Townsend (Reference Townsend1956), this state is achieved if the streamwise velocity at the edge of the boundary layer
$\unicode[STIX]{x1D6FD}_{K}=(\unicode[STIX]{x1D6FF}_{K}^{\ast }/\overline{\unicode[STIX]{x1D70F}}_{w})\,(\text{d}p_{e}/\text{d}x)$
, which must be constant for all streamwise positions. Following the idea of Townsend (Reference Townsend1956), this state is achieved if the streamwise velocity at the edge of the boundary layer
![]() $u_{e}$
follows the power-law relation
$u_{e}$
follows the power-law relation
![]() $u_{PG}(x)=\unicode[STIX]{x1D6FC}(x-x_{origin})^{m}$
, with the PG strength exponent
$u_{PG}(x)=\unicode[STIX]{x1D6FC}(x-x_{origin})^{m}$
, with the PG strength exponent
![]() $m$
, a scaling parameter
$m$
, a scaling parameter
![]() $\unicode[STIX]{x1D6FC}=u_{PG}(x_{PG,start})$
and the virtual origin of the boundary layer
$\unicode[STIX]{x1D6FC}=u_{PG}(x_{PG,start})$
and the virtual origin of the boundary layer
![]() $x_{origin}$
. Based on the analytical investigations and the assumptions made therein, both definitions are assumed to approximately still hold for the compressible regime, see Gibis et al. (Reference Gibis, Wenzel, Kloker and Rist2019).
$x_{origin}$
. Based on the analytical investigations and the assumptions made therein, both definitions are assumed to approximately still hold for the compressible regime, see Gibis et al. (Reference Gibis, Wenzel, Kloker and Rist2019).
The corresponding temperature and pressure distributions are calculated from the one-dimensional isentropic gas equations
 $$\begin{eqnarray}T_{PG}(x)=T_{t}-\frac{\displaystyle \frac{\unicode[STIX]{x1D6FE}-1}{2}u_{PG}(x)^{2}}{\unicode[STIX]{x1D6FE}R},\quad p_{PG}(x)=\frac{p_{t}}{\displaystyle \left(1+\frac{\unicode[STIX]{x1D6FE}-1}{2}M_{PG}(x)^{2}\right)^{\unicode[STIX]{x1D6FE}/(\unicode[STIX]{x1D6FE}-1)}},\end{eqnarray}$$
$$\begin{eqnarray}T_{PG}(x)=T_{t}-\frac{\displaystyle \frac{\unicode[STIX]{x1D6FE}-1}{2}u_{PG}(x)^{2}}{\unicode[STIX]{x1D6FE}R},\quad p_{PG}(x)=\frac{p_{t}}{\displaystyle \left(1+\frac{\unicode[STIX]{x1D6FE}-1}{2}M_{PG}(x)^{2}\right)^{\unicode[STIX]{x1D6FE}/(\unicode[STIX]{x1D6FE}-1)}},\end{eqnarray}$$
with the Mach number
![]() $M_{PG}^{2}=u_{PG}^{2}/(\unicode[STIX]{x1D6FE}RT_{PG})$
, the total temperature
$M_{PG}^{2}=u_{PG}^{2}/(\unicode[STIX]{x1D6FE}RT_{PG})$
, the total temperature
![]() $T_{t}$
and total pressure
$T_{t}$
and total pressure
![]() $p_{t}$
calculated at the inflow of the simulation domain as well as the isentropic exponent
$p_{t}$
calculated at the inflow of the simulation domain as well as the isentropic exponent
![]() $\unicode[STIX]{x1D6FE}$
. The distribution of the far-field density is calculated from the equation of state
$\unicode[STIX]{x1D6FE}$
. The distribution of the far-field density is calculated from the equation of state
![]() $\unicode[STIX]{x1D70C}_{PG}=p_{PG}/(RT_{PG})$
. The particular values describing the respective velocity and thus the pressure distributions are summarized in table 1. Note that the definition of the pressure distribution at the top of the simulation domain yielding a requested
$\unicode[STIX]{x1D70C}_{PG}=p_{PG}/(RT_{PG})$
. The particular values describing the respective velocity and thus the pressure distributions are summarized in table 1. Note that the definition of the pressure distribution at the top of the simulation domain yielding a requested
![]() $\unicode[STIX]{x1D6FD}_{K}$
-value is the result of an iterative procedure, since both the correlation between
$\unicode[STIX]{x1D6FD}_{K}$
-value is the result of an iterative procedure, since both the correlation between
![]() $m$
and
$m$
and
![]() $\unicode[STIX]{x1D6FD}_{K}$
as well as the exact value of
$\unicode[STIX]{x1D6FD}_{K}$
as well as the exact value of
![]() $x_{origin}$
are unknown a priori.
$x_{origin}$
are unknown a priori.
Table 1. Initial values for the PG cases. Given parameters are the starting point of the PG region in boundary-layer thicknesses at the inflow of the domain
![]() $\unicode[STIX]{x1D6FF}_{99,0}$
, the virtual origin of the velocity distribution
$\unicode[STIX]{x1D6FF}_{99,0}$
, the virtual origin of the velocity distribution
![]() $x_{origin}$
, the PG strength exponent
$x_{origin}$
, the PG strength exponent
![]() $m$
, smoothed regions between ZPG and PG regions and the resulting
$m$
, smoothed regions between ZPG and PG regions and the resulting
![]() $\unicode[STIX]{x1D6FD}_{K}$
and
$\unicode[STIX]{x1D6FD}_{K}$
and
![]() $\unicode[STIX]{x1D6FD}$
parameters, if computed with the incompressible and compressible displacement thicknesses
$\unicode[STIX]{x1D6FD}$
parameters, if computed with the incompressible and compressible displacement thicknesses
![]() $\unicode[STIX]{x1D6FF}_{K}^{\ast }$
and
$\unicode[STIX]{x1D6FF}_{K}^{\ast }$
and
![]() $\unicode[STIX]{x1D6FF}^{\ast }$
, respectively.
$\unicode[STIX]{x1D6FF}^{\ast }$
, respectively.

Figure 3 visualizes both the initially implied (
![]() $p_{PG}$
,
$p_{PG}$
,
![]() $u_{PG}$
) and the resulting pressure and velocity distributions after being adapted by the particular BC (
$u_{PG}$
) and the resulting pressure and velocity distributions after being adapted by the particular BC (
![]() $p_{top}$
,
$p_{top}$
,
![]() $u_{top}$
,
$u_{top}$
,
![]() $v_{top}$
), all evaluated at the top of the simulation domains. The subsonic pressure distributions are fixed by the subsonic free-stream BC to the prescribed values
$v_{top}$
), all evaluated at the top of the simulation domains. The subsonic pressure distributions are fixed by the subsonic free-stream BC to the prescribed values
![]() $p_{PG}=p_{top}$
in figure 3(a) and thus also approximately the streamwise velocity component
$p_{PG}=p_{top}$
in figure 3(a) and thus also approximately the streamwise velocity component
![]() $u_{PG}\approx u_{top}$
in figure 3(b). The supersonic initial distributions are adapted by the free-stream BC in such a way that the pressure at the far-field boundary matches the pressure of the resulting flow field inside the domain, see Franko & Lele (Reference Franko and Lele2014) and Wenzel (Reference Wenzel2019). The resulting pressure distributions still follow an approximated power-law relation (blue/cyan for the prescribed distributions
$u_{PG}\approx u_{top}$
in figure 3(b). The supersonic initial distributions are adapted by the free-stream BC in such a way that the pressure at the far-field boundary matches the pressure of the resulting flow field inside the domain, see Franko & Lele (Reference Franko and Lele2014) and Wenzel (Reference Wenzel2019). The resulting pressure distributions still follow an approximated power-law relation (blue/cyan for the prescribed distributions
![]() $p_{PG}$
, grey for the resulting distributions
$p_{PG}$
, grey for the resulting distributions
![]() $p_{top}$
, only given for the
$p_{top}$
, only given for the
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}$
and
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}$
and
![]() $cFPG_{\unicode[STIX]{x1D6FD}_{K}=-0.18}$
case). The resulting distributions for the streamwise velocity component
$cFPG_{\unicode[STIX]{x1D6FD}_{K}=-0.18}$
case). The resulting distributions for the streamwise velocity component
![]() $u_{top}$
are given in figure 3(b) and show reciprocal trends. The wall-normal velocity component
$u_{top}$
are given in figure 3(b) and show reciprocal trends. The wall-normal velocity component
![]() $v_{top}$
is given in figure 3(c). Whereas subsonic APG and supersonic FPG cases correspond to diverging nozzle flows with positive
$v_{top}$
is given in figure 3(c). Whereas subsonic APG and supersonic FPG cases correspond to diverging nozzle flows with positive
![]() $v$
-components, supersonic APG and subsonic FPG cases correspond to converging nozzle flows with negative
$v$
-components, supersonic APG and subsonic FPG cases correspond to converging nozzle flows with negative
![]() $v$
-components. It is noted that the strongest APG case decelerates the far-field flow by approximately 35 %, resulting in a maximum wall-normal velocity component
$v$
-components. It is noted that the strongest APG case decelerates the far-field flow by approximately 35 %, resulting in a maximum wall-normal velocity component
![]() $v_{top}$
of approximately 8 % of the streamwise velocity component
$v_{top}$
of approximately 8 % of the streamwise velocity component
![]() $u_{top}$
.
$u_{top}$
.
2.5 Simulation parameters
The grid resolution for all subsonic cases is based on the most restricting one which is the
![]() $iZPG$
case (
$iZPG$
case (
![]() $i$
for quasi incompressible), which thus allows the application of the same resolution criteria as for the ZPG study evaluated in Wenzel et al. (Reference Wenzel, Selent, Kloker and Rist2018b
). For all supersonic cases, the grid resolution is based on the most restricting
$i$
for quasi incompressible), which thus allows the application of the same resolution criteria as for the ZPG study evaluated in Wenzel et al. (Reference Wenzel, Selent, Kloker and Rist2018b
). For all supersonic cases, the grid resolution is based on the most restricting
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}$
case. Its grid resolution is comparable to the ZPG
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}$
case. Its grid resolution is comparable to the ZPG
![]() $M_{\infty }=2.0$
case given in Wenzel et al. (Reference Wenzel, Selent, Kloker and Rist2018b
). A grid convergence analysis for the two most restricting cases is given in appendix A. The numerical grid for the sub- and supersonic cases consists of
$M_{\infty }=2.0$
case given in Wenzel et al. (Reference Wenzel, Selent, Kloker and Rist2018b
). A grid convergence analysis for the two most restricting cases is given in appendix A. The numerical grid for the sub- and supersonic cases consists of
![]() $2500\times 270\times 820$
and
$2500\times 270\times 820$
and
![]() $5000\times 300\times 960$
grid points in the three dimensions, respectively, both with additional
$5000\times 300\times 960$
grid points in the three dimensions, respectively, both with additional
![]() $200$
points appended in the outflow region in the streamwise direction. Whereas each subsonic set-up consists of
$200$
points appended in the outflow region in the streamwise direction. Whereas each subsonic set-up consists of
![]() $597\,780\,000$
total grid points, each supersonic set-up consists of
$597\,780\,000$
total grid points, each supersonic set-up consists of
![]() $1\,497\,600\,000$
total grid points. The resulting grid resolution in wall units is summarized in table 3(b) for all cases; it is evaluated for the usable region where almost constant
$1\,497\,600\,000$
total grid points. The resulting grid resolution in wall units is summarized in table 3(b) for all cases; it is evaluated for the usable region where almost constant
![]() $\unicode[STIX]{x1D6FD}_{K}$
-values can be found, see figure 10. Table 3(a) summarizes additional information characterizing the spatial extent of the numerical simulation domain for all cases. The reference thermodynamic flow properties are the inflow far-field temperature
$\unicode[STIX]{x1D6FD}_{K}$
-values can be found, see figure 10. Table 3(a) summarizes additional information characterizing the spatial extent of the numerical simulation domain for all cases. The reference thermodynamic flow properties are the inflow far-field temperature
![]() $T_{\infty }=288.15~\text{K}$
, inflow far-field density
$T_{\infty }=288.15~\text{K}$
, inflow far-field density
![]() $\unicode[STIX]{x1D70C}_{PG,\infty }=1.225~\text{kg}~\text{m}^{-3}$
, Prandtl number
$\unicode[STIX]{x1D70C}_{PG,\infty }=1.225~\text{kg}~\text{m}^{-3}$
, Prandtl number
![]() $Pr=0.71$
, specific gas constant
$Pr=0.71$
, specific gas constant
![]() $R=287~\text{J}~\text{kg}^{-1}~\text{K}^{-1}$
and ratio of specific heats
$R=287~\text{J}~\text{kg}^{-1}~\text{K}^{-1}$
and ratio of specific heats
![]() $\unicode[STIX]{x1D6FE}=1.4$
and are set equal for all cases.
$\unicode[STIX]{x1D6FE}=1.4$
and are set equal for all cases.

Figure 3. (a) Pressure
![]() $p$
for subsonic cases (left axis) and supersonic cases (right axis), and (b,c)
$p$
for subsonic cases (left axis) and supersonic cases (right axis), and (b,c)
![]() $u$
- and
$u$
- and
![]() $v$
-velocity components. All distributions are evaluated at the top of the simulation domain (index ‘
$v$
-velocity components. All distributions are evaluated at the top of the simulation domain (index ‘
![]() $top$
’). Red lines correspond to subsonic, blue and cyan lines to supersonic cases. Whereas the subsonic far-field BC fixes the pressure distribution
$top$
’). Red lines correspond to subsonic, blue and cyan lines to supersonic cases. Whereas the subsonic far-field BC fixes the pressure distribution
![]() $p_{top}=p_{PG}$
, the supersonic BC allows the pressure to adapt. The initially prescribed values (index ‘
$p_{top}=p_{PG}$
, the supersonic BC allows the pressure to adapt. The initially prescribed values (index ‘
![]() $PG$
’) are represented as coloured lines, the adapted states (index ‘
$PG$
’) are represented as coloured lines, the adapted states (index ‘
![]() $top$
’) as grey lines only given for
$top$
’) as grey lines only given for
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}$
and
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}$
and
![]() $cFPG_{\unicode[STIX]{x1D6FD}_{K}=-0.18}$
.
$cFPG_{\unicode[STIX]{x1D6FD}_{K}=-0.18}$
.
Table 2. Summary of time-averaging parameters measured at the begin and end of the usable region, see figure 10.
![]() $\unicode[STIX]{x0394}tu_{e}/\unicode[STIX]{x1D6FF}^{\ast }$
and
$\unicode[STIX]{x0394}tu_{e}/\unicode[STIX]{x1D6FF}^{\ast }$
and
![]() $\unicode[STIX]{x0394}tu_{e}/\unicode[STIX]{x1D6FF}_{99}$
give the number of local boundary-layer thicknesses
$\unicode[STIX]{x0394}tu_{e}/\unicode[STIX]{x1D6FF}_{99}$
give the number of local boundary-layer thicknesses
![]() $\unicode[STIX]{x1D6FF}_{99}$
and local displacement thicknesses
$\unicode[STIX]{x1D6FF}_{99}$
and local displacement thicknesses
![]() $\unicode[STIX]{x1D6FF}^{\ast }$
, which have been streamed through during
$\unicode[STIX]{x1D6FF}^{\ast }$
, which have been streamed through during
![]() $\unicode[STIX]{x0394}t$
.
$\unicode[STIX]{x0394}t$
.
![]() $\unicode[STIX]{x0394}tu_{\unicode[STIX]{x1D70F},0}^{2}/\unicode[STIX]{x1D708}_{w}$
represents
$\unicode[STIX]{x0394}tu_{\unicode[STIX]{x1D70F},0}^{2}/\unicode[STIX]{x1D708}_{w}$
represents
![]() $\unicode[STIX]{x0394}t$
in wall units
$\unicode[STIX]{x0394}t$
in wall units
![]() $\unicode[STIX]{x0394}t^{+}$
. The number of flow-through times (FTT) gives the number of time-averaged runs through the main region.
$\unicode[STIX]{x0394}t^{+}$
. The number of flow-through times (FTT) gives the number of time-averaged runs through the main region.
![]() $\unicode[STIX]{x0394}x_{ind.}/\unicode[STIX]{x1D6FF}_{99,0}$
gives the induction distance needed to reach a fully turbulent state, see Wenzel et al. (Reference Wenzel, Selent, Kloker and Rist2018b
).
$\unicode[STIX]{x0394}x_{ind.}/\unicode[STIX]{x1D6FF}_{99,0}$
gives the induction distance needed to reach a fully turbulent state, see Wenzel et al. (Reference Wenzel, Selent, Kloker and Rist2018b
).

Table 3. Nearly incompressible cases with inflow Mach numbers of
![]() $M_{\infty ,0}=0.5$
are highlighted by red colour, supersonic cases with
$M_{\infty ,0}=0.5$
are highlighted by red colour, supersonic cases with
![]() $M_{\infty ,0}=2.0$
by blue and cyan colours. Given parameters characterize the beginning and the end of the usable region where
$M_{\infty ,0}=2.0$
by blue and cyan colours. Given parameters characterize the beginning and the end of the usable region where
![]() $\unicode[STIX]{x1D6FD}_{K}$
is almost constant, see figure 10.
$\unicode[STIX]{x1D6FD}_{K}$
is almost constant, see figure 10.

Data averaging is performed over both time and spanwise direction and does not start before the flow has passed the whole simulation domain at least twice. An overview of the time-averaging periods
![]() $\unicode[STIX]{x0394}t$
used for all cases is given in table 2. Consistently for all cases, time averages were performed over a flow-through time corresponding to approximately 250 local boundary-layer thicknesses
$\unicode[STIX]{x0394}t$
used for all cases is given in table 2. Consistently for all cases, time averages were performed over a flow-through time corresponding to approximately 250 local boundary-layer thicknesses
![]() $\unicode[STIX]{x1D6FF}_{99}$
, see
$\unicode[STIX]{x1D6FF}_{99}$
, see
![]() $\unicode[STIX]{x0394}tu_{e}/\unicode[STIX]{x1D6FF}_{99}$
in table 2.
$\unicode[STIX]{x0394}tu_{e}/\unicode[STIX]{x1D6FF}_{99}$
in table 2.
3 Results for the untransformed, compressible flow fields
No DNS data are available in the literature for the reflected-wave set-up. It is the primary goal of this section to characterize the resulting flow-field data first by evaluating the spatial evolution of essential boundary-layer quantities. Additionally, some characteristic features of the instantaneous turbulent flow fields are shortly presented; their detailed interpretation will be part of future studies. The most common compressibility transformations are evaluated and discussed in § 4.
3.1 Two- and three-dimensional flow fields
Figures 4 and 5 show the mean-pressure field
![]() $\overline{p}/p_{\infty ,0}$
and the wall-normal velocity component
$\overline{p}/p_{\infty ,0}$
and the wall-normal velocity component
![]() $\overline{v}/u_{\infty ,0}$
of (a) the strongest subsonic
$\overline{v}/u_{\infty ,0}$
of (a) the strongest subsonic
![]() $iAPG_{\unicode[STIX]{x1D6FD}_{K}=1.05}$
case, (b) the strongest supersonic
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=1.05}$
case, (b) the strongest supersonic
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}$
case and (c) the supersonic
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}$
case and (c) the supersonic
![]() $cFPG_{\unicode[STIX]{x1D6FD}_{K}=-0.18}$
case; the outflow region is cropped. The boundary-layer thickness
$cFPG_{\unicode[STIX]{x1D6FD}_{K}=-0.18}$
case; the outflow region is cropped. The boundary-layer thickness
![]() $\unicode[STIX]{x1D6FF}_{99}$
is depicted by black dash-dotted lines.
$\unicode[STIX]{x1D6FF}_{99}$
is depicted by black dash-dotted lines.
A fully developed pressure field – characterized by lines of constant pressure along
![]() $y$
outside the boundary layer (black solid lines) – is achieved for the subsonic
$y$
outside the boundary layer (black solid lines) – is achieved for the subsonic
![]() $iAPG_{\unicode[STIX]{x1D6FD}_{K}=1.05}$
case for
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=1.05}$
case for
![]() $x/\unicode[STIX]{x1D6FF}_{99,0}\gtrapprox 50$
(figure 4
a). For the supersonic cases, this induction distance is elongated up to
$x/\unicode[STIX]{x1D6FF}_{99,0}\gtrapprox 50$
(figure 4
a). For the supersonic cases, this induction distance is elongated up to
![]() $x/\unicode[STIX]{x1D6FF}_{99,0}\gtrapprox 200$
, see figure 4(b,c) and p. 245. Both the subsonic
$x/\unicode[STIX]{x1D6FF}_{99,0}\gtrapprox 200$
, see figure 4(b,c) and p. 245. Both the subsonic
![]() $iAPG_{\unicode[STIX]{x1D6FD}_{K}=1.05}$
case in figure 5(a) and the supersonic
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=1.05}$
case in figure 5(a) and the supersonic
![]() $cFPG_{\unicode[STIX]{x1D6FD}_{K}=-0.18}$
case in figure 5(c) are characterized by positive wall-normal velocity components
$cFPG_{\unicode[STIX]{x1D6FD}_{K}=-0.18}$
case in figure 5(c) are characterized by positive wall-normal velocity components
![]() $\overline{v}/u_{\infty ,0}$
at the top of the simulation domain, while the supersonic
$\overline{v}/u_{\infty ,0}$
at the top of the simulation domain, while the supersonic
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}$
case in figure 5(b) is characterized by negative
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}$
case in figure 5(b) is characterized by negative
![]() $\overline{v}/u_{\infty ,0}$
. Note, however, that
$\overline{v}/u_{\infty ,0}$
. Note, however, that
![]() $\overline{v}/u_{\infty ,0}$
is almost completely positive inside the boundary layer for the supersonic
$\overline{v}/u_{\infty ,0}$
is almost completely positive inside the boundary layer for the supersonic
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}$
case. This is caused by the strong deceleration of the supersonic flow where the subsonic displacing behaviour dominates the boundary layer; compare the red solid
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}$
case. This is caused by the strong deceleration of the supersonic flow where the subsonic displacing behaviour dominates the boundary layer; compare the red solid
![]() $\overline{v}=0$
and black dash-dotted
$\overline{v}=0$
and black dash-dotted
![]() $\unicode[STIX]{x1D6FF}_{99}$
-lines.
$\unicode[STIX]{x1D6FF}_{99}$
-lines.

Figure 4. Mean-flow pressure field
![]() $\overline{p}/p_{\infty ,0}$
for (a) the strongest subsonic
$\overline{p}/p_{\infty ,0}$
for (a) the strongest subsonic
![]() $iAPG_{\unicode[STIX]{x1D6FD}_{K}=1.05}$
case, (b) the strongest supersonic
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=1.05}$
case, (b) the strongest supersonic
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}$
case and (c) the supersonic
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}$
case and (c) the supersonic
![]() $cFPG_{\unicode[STIX]{x1D6FD}_{K}=-0.18}$
case.
$cFPG_{\unicode[STIX]{x1D6FD}_{K}=-0.18}$
case.

Figure 5. Mean-flow field of the wall-normal velocity component
![]() $\overline{v}/u_{\infty ,0}$
for (a) the strongest subsonic
$\overline{v}/u_{\infty ,0}$
for (a) the strongest subsonic
![]() $iAPG_{\unicode[STIX]{x1D6FD}_{K}=1.05}$
case, the strongest supersonic
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=1.05}$
case, the strongest supersonic
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}$
case and the supersonic
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}$
case and the supersonic
![]() $cFPG_{\unicode[STIX]{x1D6FD}_{K}=-0.18}$
case.
$cFPG_{\unicode[STIX]{x1D6FD}_{K}=-0.18}$
case.
Snapshots of the streamwise velocity component
![]() $u/u_{e}(x)$
are given in figures 6 and 7 for a subset of the simulation domain extracted at
$u/u_{e}(x)$
are given in figures 6 and 7 for a subset of the simulation domain extracted at
![]() $Re_{\unicode[STIX]{x1D70F}}=490$
(FPG at
$Re_{\unicode[STIX]{x1D70F}}=490$
(FPG at
![]() $Re_{\unicode[STIX]{x1D70F}}=360$
) to get an impression of the unsteady flow fields, see also figures 29 and 30. While the subsonic
$Re_{\unicode[STIX]{x1D70F}}=360$
) to get an impression of the unsteady flow fields, see also figures 29 and 30. While the subsonic
![]() $iZPG$
and
$iZPG$
and
![]() $iAPG_{\unicode[STIX]{x1D6FD}_{K}=1.05}$
cases are depicted in figure 6(a,b), respectively, the supersonic
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=1.05}$
cases are depicted in figure 6(a,b), respectively, the supersonic
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}$
,
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}$
,
![]() $cZPG$
and
$cZPG$
and
![]() $cFPG_{\unicode[STIX]{x1D6FD}_{K}=-0.18}$
cases are depicted in figure 7(a,b,c), respectively. The time-averaged boundary-layer thickness
$cFPG_{\unicode[STIX]{x1D6FD}_{K}=-0.18}$
cases are depicted in figure 7(a,b,c), respectively. The time-averaged boundary-layer thickness
![]() $\overline{\unicode[STIX]{x1D6FF}}_{99}$
(only emphasized in the present plots with an overbar) and the instantaneous boundary-layer thickness
$\overline{\unicode[STIX]{x1D6FF}}_{99}$
(only emphasized in the present plots with an overbar) and the instantaneous boundary-layer thickness
![]() $\unicode[STIX]{x1D6FF}_{99}$
are depicted as blue dash-dotted and solid lines, respectively. Grey iso-lines represent nine equidistantly distributed levels of the streamwise velocity component
$\unicode[STIX]{x1D6FF}_{99}$
are depicted as blue dash-dotted and solid lines, respectively. Grey iso-lines represent nine equidistantly distributed levels of the streamwise velocity component
![]() $u/u_{e}(x)$
between
$u/u_{e}(x)$
between
![]() $0.1$
and
$0.1$
and
![]() $0.9$
. Solely for the supersonic cases in figure 7, the instantaneous sonic line is depicted as a black bold solid line.
$0.9$
. Solely for the supersonic cases in figure 7, the instantaneous sonic line is depicted as a black bold solid line.

Figure 6. Snapshots of the streamwise velocity component
![]() $u/u_{\infty ,0}$
for the (a) subsonic
$u/u_{\infty ,0}$
for the (a) subsonic
![]() $iZPG$
case and the (b) strongest subsonic
$iZPG$
case and the (b) strongest subsonic
![]() $iAPG_{\unicode[STIX]{x1D6FD}_{K}=1.05}$
case at
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=1.05}$
case at
![]() $Re_{\unicode[STIX]{x1D70F}}=490$
. Left plots:
$Re_{\unicode[STIX]{x1D70F}}=490$
. Left plots:
![]() $xy$
-plane. Right plots:
$xy$
-plane. Right plots:
![]() $zy$
-plane.
$zy$
-plane.

Figure 7. Snapshots of the streamwise velocity component
![]() $u/u_{\infty ,0}$
for (a) the supersonic
$u/u_{\infty ,0}$
for (a) the supersonic
![]() $cFPG_{\unicode[STIX]{x1D6FD}_{K}=-0.18}$
case, (b) the supersonic
$cFPG_{\unicode[STIX]{x1D6FD}_{K}=-0.18}$
case, (b) the supersonic
![]() $cZPG$
case and (c) the strongest supersonic
$cZPG$
case and (c) the strongest supersonic
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}$
case at
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}$
case at
![]() $Re_{\unicode[STIX]{x1D70F}}=490$
(FPG at
$Re_{\unicode[STIX]{x1D70F}}=490$
(FPG at
![]() $Re_{\unicode[STIX]{x1D70F}}=360$
). Left plots:
$Re_{\unicode[STIX]{x1D70F}}=360$
). Left plots:
![]() $xy$
-plane. Right plots:
$xy$
-plane. Right plots:
![]() $zy$
-plane. The sonic line representing
$zy$
-plane. The sonic line representing
![]() $M=1$
is depicted as black bold line.
$M=1$
is depicted as black bold line.

Figure 8. Snapshots of vortices by iso-surfaces of the
![]() $\unicode[STIX]{x1D706}_{2}$
-criterion with
$\unicode[STIX]{x1D706}_{2}$
-criterion with
![]() $\unicode[STIX]{x1D706}_{2}=-0.05u_{e}(x)/u_{\infty ,0}$
for (a) the subsonic
$\unicode[STIX]{x1D706}_{2}=-0.05u_{e}(x)/u_{\infty ,0}$
for (a) the subsonic
![]() $iZPG$
case and (b) the strongest subsonic
$iZPG$
case and (b) the strongest subsonic
![]() $iAPG_{\unicode[STIX]{x1D6FD}_{K}=1.05}$
case at
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=1.05}$
case at
![]() $Re_{\unicode[STIX]{x1D70F}}=490$
. Colour depicts the fluctuation amplitude of the streamwise velocity component
$Re_{\unicode[STIX]{x1D70F}}=490$
. Colour depicts the fluctuation amplitude of the streamwise velocity component
![]() $u^{\prime }/u_{\infty ,0}$
. Left plots: subset of the simulation domain in top view. Right plots: close-ups of the white bordered regions in the left plots, see also figures 29 and 30.
$u^{\prime }/u_{\infty ,0}$
. Left plots: subset of the simulation domain in top view. Right plots: close-ups of the white bordered regions in the left plots, see also figures 29 and 30.

Figure 9. Snapshots of vortices by iso-surfaces of the
![]() $\unicode[STIX]{x1D706}_{2}$
-criterion with
$\unicode[STIX]{x1D706}_{2}$
-criterion with
![]() $\unicode[STIX]{x1D706}_{2}=-0.05u_{e}(x)/u_{\infty ,0}$
for (a) the supersonic
$\unicode[STIX]{x1D706}_{2}=-0.05u_{e}(x)/u_{\infty ,0}$
for (a) the supersonic
![]() $cFPG_{\unicode[STIX]{x1D6FD}_{K}=-0.18}$
case, (b) the supersonic
$cFPG_{\unicode[STIX]{x1D6FD}_{K}=-0.18}$
case, (b) the supersonic
![]() $cZPG$
case and (c) the strongest supersonic
$cZPG$
case and (c) the strongest supersonic
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}$
case at
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}$
case at
![]() $Re_{\unicode[STIX]{x1D70F}}=490$
(FPG at
$Re_{\unicode[STIX]{x1D70F}}=490$
(FPG at
![]() $Re_{\unicode[STIX]{x1D70F}}=360$
). Colour depicts the fluctuation amplitude of the streamwise velocity component
$Re_{\unicode[STIX]{x1D70F}}=360$
). Colour depicts the fluctuation amplitude of the streamwise velocity component
![]() $u^{\prime }/u_{\infty ,0}$
in the same representation as in figure 8, see also figures 29 and 30.
$u^{\prime }/u_{\infty ,0}$
in the same representation as in figure 8, see also figures 29 and 30.
Compared with the incompressible
![]() $iZPG$
case in figure 6(a), the subsonic APG case shows a coarsening of turbulent structures with increasing APG strength, see figure 6(b). For the supersonic cases in figure 7 the inverse trend is found, turbulent structures are refined for the APG case (figure 7
c) and coarsened for the FPG (figure 7
a) in comparison to the ZPG case (figure 7
b). Whereas the sonic line is pushed to the wall for the supersonic FPG case, it is lifted for the APG case in the streamwise direction. Details will be discussed in the following sections.
$iZPG$
case in figure 6(a), the subsonic APG case shows a coarsening of turbulent structures with increasing APG strength, see figure 6(b). For the supersonic cases in figure 7 the inverse trend is found, turbulent structures are refined for the APG case (figure 7
c) and coarsened for the FPG (figure 7
a) in comparison to the ZPG case (figure 7
b). Whereas the sonic line is pushed to the wall for the supersonic FPG case, it is lifted for the APG case in the streamwise direction. Details will be discussed in the following sections.
Figures 8 and 9 illustrate iso-levels of the
![]() $\unicode[STIX]{x1D706}_{2}$
-criterion computed from the non-dimensionalized flow field
$\unicode[STIX]{x1D706}_{2}$
-criterion computed from the non-dimensionalized flow field
![]() $u_{i}=u_{i}/u_{\infty ,0}$
with
$u_{i}=u_{i}/u_{\infty ,0}$
with
![]() $\unicode[STIX]{x1D706}_{2}=-0.05\,u_{e}(x)/u_{\infty ,0}$
for the previously discussed cases. Snapshots of the complete simulation domain are given in figures 29 and 30. In accordance with the instantaneous velocity fields given before, the
$\unicode[STIX]{x1D706}_{2}=-0.05\,u_{e}(x)/u_{\infty ,0}$
for the previously discussed cases. Snapshots of the complete simulation domain are given in figures 29 and 30. In accordance with the instantaneous velocity fields given before, the
![]() $\unicode[STIX]{x1D706}_{2}$
-structures are thinned out for APGs in the subsonic and FPGs in the supersonic regime, and refined by APGs in the supersonic regime if compared to the respective ZPG case. A detailed investigation of compressible PG effects on the turbulent structures will be part of future studies.
$\unicode[STIX]{x1D706}_{2}$
-structures are thinned out for APGs in the subsonic and FPGs in the supersonic regime, and refined by APGs in the supersonic regime if compared to the respective ZPG case. A detailed investigation of compressible PG effects on the turbulent structures will be part of future studies.
3.2 Boundary-layer characterization
In this section the evolution of the most important boundary-layer quantities is described.
3.2.1 Evaluation of the Rotta–Clauser parameter
Both the kinematic and the compressible results of the Rotta–Clauser parameter
![]() $\unicode[STIX]{x1D6FD}_{(K)}=(\unicode[STIX]{x1D6FF}_{(K)}^{\ast }/\overline{\unicode[STIX]{x1D70F}}_{w})(\text{d}p_{e}/\text{d}x)$
are shown in figure 10, where the kinematic displacement thickness is
$\unicode[STIX]{x1D6FD}_{(K)}=(\unicode[STIX]{x1D6FF}_{(K)}^{\ast }/\overline{\unicode[STIX]{x1D70F}}_{w})(\text{d}p_{e}/\text{d}x)$
are shown in figure 10, where the kinematic displacement thickness is
![]() $\unicode[STIX]{x1D6FF}_{K}^{\ast }=\int _{0}^{\unicode[STIX]{x1D6FF}_{99}}(1-\overline{u}/u_{e})\,\text{d}y$
and the compressible displacement thickness
$\unicode[STIX]{x1D6FF}_{K}^{\ast }=\int _{0}^{\unicode[STIX]{x1D6FF}_{99}}(1-\overline{u}/u_{e})\,\text{d}y$
and the compressible displacement thickness
![]() $\unicode[STIX]{x1D6FF}^{\ast }=\int _{0}^{\unicode[STIX]{x1D6FF}_{99}}(1-(\overline{\unicode[STIX]{x1D70C}}\,\overline{u})/(\unicode[STIX]{x1D70C}_{e}u_{e}))\,\text{d}y$
. It is shown in Part 2 of this study (Gibis et al.
Reference Gibis, Wenzel, Kloker and Rist2019) and by the DNS results discussed below that the
$\unicode[STIX]{x1D6FF}^{\ast }=\int _{0}^{\unicode[STIX]{x1D6FF}_{99}}(1-(\overline{\unicode[STIX]{x1D70C}}\,\overline{u})/(\unicode[STIX]{x1D70C}_{e}u_{e}))\,\text{d}y$
. It is shown in Part 2 of this study (Gibis et al.
Reference Gibis, Wenzel, Kloker and Rist2019) and by the DNS results discussed below that the
![]() $\unicode[STIX]{x1D6FD}_{K}$
-parameter correctly characterizes the self-similar state of the compressible TBL and hence enables a comparison of PG influences between compressible and incompressible flows. The compressible definition
$\unicode[STIX]{x1D6FD}_{K}$
-parameter correctly characterizes the self-similar state of the compressible TBL and hence enables a comparison of PG influences between compressible and incompressible flows. The compressible definition
![]() $\unicode[STIX]{x1D6FD}$
turns out to be less relevant because the compressible displacement thickness is not a good characterizing length scale for the outer part of the boundary layer, as shown in Gibis et al. (Reference Gibis, Wenzel, Kloker and Rist2019). Since all simulations start with a ZPG region at the inflow (see § 2.4), an induction distance is needed before the individual
$\unicode[STIX]{x1D6FD}$
turns out to be less relevant because the compressible displacement thickness is not a good characterizing length scale for the outer part of the boundary layer, as shown in Gibis et al. (Reference Gibis, Wenzel, Kloker and Rist2019). Since all simulations start with a ZPG region at the inflow (see § 2.4), an induction distance is needed before the individual
![]() $\unicode[STIX]{x1D6FD}_{(K)}$
-values become approximately constant (grey dashed lines). Expressed in various Reynolds numbers, the start and the end of the (almost) constant regions are summarized in table 3(a) for all cases.
$\unicode[STIX]{x1D6FD}_{(K)}$
-values become approximately constant (grey dashed lines). Expressed in various Reynolds numbers, the start and the end of the (almost) constant regions are summarized in table 3(a) for all cases.

Figure 10. Clauser parameters
![]() $\unicode[STIX]{x1D6FD}_{(K)}=(\unicode[STIX]{x1D6FF}_{(K)}^{\ast }/\overline{\unicode[STIX]{x1D70F}}_{w})(\text{d}p_{e}/\text{d}x)$
for the computed results. Red lines represent the four subsonic cases, blue and cyan lines the six supersonic cases. Coloured horizontal lines represent curve fits of their solid line counterparts. Grey dashed lines represent induction regions, where
$\unicode[STIX]{x1D6FD}_{(K)}=(\unicode[STIX]{x1D6FF}_{(K)}^{\ast }/\overline{\unicode[STIX]{x1D70F}}_{w})(\text{d}p_{e}/\text{d}x)$
for the computed results. Red lines represent the four subsonic cases, blue and cyan lines the six supersonic cases. Coloured horizontal lines represent curve fits of their solid line counterparts. Grey dashed lines represent induction regions, where
![]() $\unicode[STIX]{x1D6FD}_{(K)}$
is not yet constant. Expressed in various Reynolds numbers, both the start and the end of the coloured regions are summarized in table 3(a) for all cases.
$\unicode[STIX]{x1D6FD}_{(K)}$
is not yet constant. Expressed in various Reynolds numbers, both the start and the end of the coloured regions are summarized in table 3(a) for all cases.
An evaluation of the resulting
![]() $\unicode[STIX]{x1D6FD}_{(K)}$
-values in figure 10 yields almost perfectly constant values for the subsonic APG cases, slightly rising values for the supersonic APG cases and slightly decreasing values for the supersonic FPG case. Due to the additional consideration of density variations in the wall-normal direction,
$\unicode[STIX]{x1D6FD}_{(K)}$
-values in figure 10 yields almost perfectly constant values for the subsonic APG cases, slightly rising values for the supersonic APG cases and slightly decreasing values for the supersonic FPG case. Due to the additional consideration of density variations in the wall-normal direction,
![]() $\unicode[STIX]{x1D6FD}$
-values are increased compared to the
$\unicode[STIX]{x1D6FD}$
-values are increased compared to the
![]() $\unicode[STIX]{x1D6FD}_{K}$
-values. As shown in the next section,
$\unicode[STIX]{x1D6FD}_{K}$
-values. As shown in the next section,
![]() $\unicode[STIX]{x1D6FF}_{K}^{\ast }$
and
$\unicode[STIX]{x1D6FF}_{K}^{\ast }$
and
![]() $\unicode[STIX]{x1D6FF}^{\ast }$
and thus also
$\unicode[STIX]{x1D6FF}^{\ast }$
and thus also
![]() $\unicode[STIX]{x1D6FD}_{K}$
and
$\unicode[STIX]{x1D6FD}_{K}$
and
![]() $\unicode[STIX]{x1D6FD}$
are not proportional to each other in their streamwise evolution for the supersonic cases due to the varying influence of compressibility. The
$\unicode[STIX]{x1D6FD}$
are not proportional to each other in their streamwise evolution for the supersonic cases due to the varying influence of compressibility. The
![]() $\unicode[STIX]{x1D6FD}_{K}$
-distributions are therefore slightly steeper compared to
$\unicode[STIX]{x1D6FD}_{K}$
-distributions are therefore slightly steeper compared to
![]() $\unicode[STIX]{x1D6FD}$
. Whereas the subsonic cases are characterized by
$\unicode[STIX]{x1D6FD}$
. Whereas the subsonic cases are characterized by
![]() $\unicode[STIX]{x1D6FD}_{K}=0.19$
, 0.58 and 1.05, the supersonic cases yield
$\unicode[STIX]{x1D6FD}_{K}=0.19$
, 0.58 and 1.05, the supersonic cases yield
![]() $\unicode[STIX]{x1D6FD}_{K}=0.15$
, 0.42, 0.55 and 0.69 for the APG and
$\unicode[STIX]{x1D6FD}_{K}=0.15$
, 0.42, 0.55 and 0.69 for the APG and
![]() $\unicode[STIX]{x1D6FD}_{K}=-0.18$
for the FPG case. The corresponding
$\unicode[STIX]{x1D6FD}_{K}=-0.18$
for the FPG case. The corresponding
![]() $\unicode[STIX]{x1D6FD}$
-parameters are summarized in table 1.
$\unicode[STIX]{x1D6FD}$
-parameters are summarized in table 1.
Constant
![]() $\unicode[STIX]{x1D6FD}_{K}$
-values mainly characterize the resulting mean flow but do not inevitably warrant perfect self-similarity of higher moments in the streamwise direction, since influences resulting from history effects occurring in the induction sections cannot be excluded. Nevertheless, the achieved constancy of the distributions suggests an approximated state of local self-similarity for all PG cases for at least 50 average boundary-layer thicknesses
$\unicode[STIX]{x1D6FD}_{K}$
-values mainly characterize the resulting mean flow but do not inevitably warrant perfect self-similarity of higher moments in the streamwise direction, since influences resulting from history effects occurring in the induction sections cannot be excluded. Nevertheless, the achieved constancy of the distributions suggests an approximated state of local self-similarity for all PG cases for at least 50 average boundary-layer thicknesses
![]() $\unicode[STIX]{x1D6FF}_{99,av}$
but not exactly for
$\unicode[STIX]{x1D6FF}_{99,av}$
but not exactly for
![]() $x\rightarrow \infty$
. Detailed investigations are given in Gibis et al. (Reference Gibis, Wenzel, Kloker and Rist2019).
$x\rightarrow \infty$
. Detailed investigations are given in Gibis et al. (Reference Gibis, Wenzel, Kloker and Rist2019).
3.2.2 Evolution of the boundary layer

Figure 11. Boundary-layer values for regions of constant
![]() $\unicode[STIX]{x1D6FD}_{(K)}$
. Subsonic and supersonic cases are coloured red and blue, respectively, the supersonic FPG case cyan. Depicted are (a) the boundary-layer thickness
$\unicode[STIX]{x1D6FD}_{(K)}$
. Subsonic and supersonic cases are coloured red and blue, respectively, the supersonic FPG case cyan. Depicted are (a) the boundary-layer thickness
![]() $\unicode[STIX]{x1D6FF}_{99}/\unicode[STIX]{x1D6FF}_{99,0}$
and the sonic lines in green solely for the supersonic cases; (b,c) the momentum thickness
$\unicode[STIX]{x1D6FF}_{99}/\unicode[STIX]{x1D6FF}_{99,0}$
and the sonic lines in green solely for the supersonic cases; (b,c) the momentum thickness
![]() $\unicode[STIX]{x1D703}/\unicode[STIX]{x1D6FF}_{99}$
(symbols, left
$\unicode[STIX]{x1D703}/\unicode[STIX]{x1D6FF}_{99}$
(symbols, left
![]() $y$
-axis) and the displacement thickness
$y$
-axis) and the displacement thickness
![]() $\unicode[STIX]{x1D6FF}^{\ast }/\unicode[STIX]{x1D6FF}_{99,0}$
(lines, right
$\unicode[STIX]{x1D6FF}^{\ast }/\unicode[STIX]{x1D6FF}_{99,0}$
(lines, right
![]() $y$
-axis) for the sub- and supersonic cases, respectively;
$y$
-axis) for the sub- and supersonic cases, respectively;
![]() $(d)$
the kinematic momentum thickness
$(d)$
the kinematic momentum thickness
![]() $\unicode[STIX]{x1D703}_{K}/\unicode[STIX]{x1D6FF}_{99}$
and the kinematic displacement thickness
$\unicode[STIX]{x1D703}_{K}/\unicode[STIX]{x1D6FF}_{99}$
and the kinematic displacement thickness
![]() $\unicode[STIX]{x1D6FF}_{K}^{\ast }/\unicode[STIX]{x1D6FF}_{99}$
solely for the supersonic cases.
$\unicode[STIX]{x1D6FF}_{K}^{\ast }/\unicode[STIX]{x1D6FF}_{99}$
solely for the supersonic cases.
All supersonic APG cases follow the same qualitative trends; thus only the cases
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.42}$
and
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.42}$
and
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}$
are depicted.
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}$
are depicted.
Figure 11(a) illustrates the spatial evolution of the boundary-layer thickness
![]() $\unicode[STIX]{x1D6FF}_{99}/\unicode[STIX]{x1D6FF}_{99,0}$
and the wall-normal position of the sonic line
$\unicode[STIX]{x1D6FF}_{99}/\unicode[STIX]{x1D6FF}_{99,0}$
and the wall-normal position of the sonic line
![]() $\unicode[STIX]{x1D6FF}_{SL}/\unicode[STIX]{x1D6FF}_{99,0}$
in green (line style in accordance with the boundary-layer thickness), the latter of which separates sub- and supersonic parts of the supersonic boundary-layer cases. The ratios of the boundary-layer thicknesses
$\unicode[STIX]{x1D6FF}_{SL}/\unicode[STIX]{x1D6FF}_{99,0}$
in green (line style in accordance with the boundary-layer thickness), the latter of which separates sub- and supersonic parts of the supersonic boundary-layer cases. The ratios of the boundary-layer thicknesses
![]() $\unicode[STIX]{x1D703}/\unicode[STIX]{x1D6FF}_{99}$
and
$\unicode[STIX]{x1D703}/\unicode[STIX]{x1D6FF}_{99}$
and
![]() $\unicode[STIX]{x1D6FF}^{\ast }/\unicode[STIX]{x1D6FF}_{99}$
are depicted in figures 11(b) and 11(c) for the sub- and supersonic cases, respectively. Solely for the supersonic cases, the ratios of the kinematic boundary-layer thicknesses are given in figure 11(d). For all three panels (b,c,d), results depicted by symbols belong to the
$\unicode[STIX]{x1D6FF}^{\ast }/\unicode[STIX]{x1D6FF}_{99}$
are depicted in figures 11(b) and 11(c) for the sub- and supersonic cases, respectively. Solely for the supersonic cases, the ratios of the kinematic boundary-layer thicknesses are given in figure 11(d). For all three panels (b,c,d), results depicted by symbols belong to the
![]() $y$
-axis located on the left-hand side of the plot; results depicted by lines belong to the
$y$
-axis located on the left-hand side of the plot; results depicted by lines belong to the
![]() $y$
-axis located on the right-hand side of the plot.
$y$
-axis located on the right-hand side of the plot.
For the quasi-incompressible cases, the boundary-layer thickens strongly with increasing APG strength (figure 11
a) resulting in a maximum of twice the thickness of the ZPG case for the
![]() $iAPG_{\unicode[STIX]{x1D6FD}_{K}=1.05}$
case. When the pressure rises in subsonic flows, the velocity decreases more rapidly than the density increases. This results in a decompression of the streamtubes and thus an increase in the boundary-layer thickness (Spina, Smits & Robinson Reference Spina, Smits and Robinson1994).
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=1.05}$
case. When the pressure rises in subsonic flows, the velocity decreases more rapidly than the density increases. This results in a decompression of the streamtubes and thus an increase in the boundary-layer thickness (Spina, Smits & Robinson Reference Spina, Smits and Robinson1994).
Given in figure 11(b), the ratio of the momentum thickness
![]() $\unicode[STIX]{x1D703}/\unicode[STIX]{x1D6FF}_{99}$
(red symbols, left
$\unicode[STIX]{x1D703}/\unicode[STIX]{x1D6FF}_{99}$
(red symbols, left
![]() $y$
-axis) as well as the ratio of the displacement thickness
$y$
-axis) as well as the ratio of the displacement thickness
![]() $\unicode[STIX]{x1D6FF}^{\ast }/\unicode[STIX]{x1D6FF}_{99}$
(red lines, right
$\unicode[STIX]{x1D6FF}^{\ast }/\unicode[STIX]{x1D6FF}_{99}$
(red lines, right
![]() $y$
-axis) are almost constant and thus almost proportional to each other in the streamwise direction,
$y$
-axis) are almost constant and thus almost proportional to each other in the streamwise direction,
![]() $\unicode[STIX]{x1D6FF}_{99}\propto \unicode[STIX]{x1D6FF}^{\ast }\propto \unicode[STIX]{x1D703}$
. As a consequence, also the shape factor
$\unicode[STIX]{x1D6FF}_{99}\propto \unicode[STIX]{x1D6FF}^{\ast }\propto \unicode[STIX]{x1D703}$
. As a consequence, also the shape factor
![]() $H=\unicode[STIX]{x1D6FF}^{\ast }/\unicode[STIX]{x1D703}$
is almost constant as will be further discussed in § 3.3.1.
$H=\unicode[STIX]{x1D6FF}^{\ast }/\unicode[STIX]{x1D703}$
is almost constant as will be further discussed in § 3.3.1.
For the compressible, supersonic APG cases, the boundary-layer thickness
![]() $\unicode[STIX]{x1D6FF}_{99}/\unicode[STIX]{x1D6FF}_{99,0}$
is first reduced and then increased compared to the
$\unicode[STIX]{x1D6FF}_{99}/\unicode[STIX]{x1D6FF}_{99,0}$
is first reduced and then increased compared to the
![]() $cZPG$
case and thus leads to an intersection point, see figure 11(a). Following Spina et al.’s (Reference Spina, Smits and Robinson1994) argument, this counterintuitive behaviour is caused by the unique character of the supersonic boundary layer that consists of both sub- and supersonic regions. In contrast to the subsonic regions, the density increases more rapidly than the velocity decreases in supersonic regions for APGs, meaning that streamtubes are compressed in the supersonic part above the green sonic line and decompressed in the subsonic part below the sonic line. When the subsonic region of the boundary layer becomes large, which means that the sonic line is noticeably lifted off the wall (approximately for
$cZPG$
case and thus leads to an intersection point, see figure 11(a). Following Spina et al.’s (Reference Spina, Smits and Robinson1994) argument, this counterintuitive behaviour is caused by the unique character of the supersonic boundary layer that consists of both sub- and supersonic regions. In contrast to the subsonic regions, the density increases more rapidly than the velocity decreases in supersonic regions for APGs, meaning that streamtubes are compressed in the supersonic part above the green sonic line and decompressed in the subsonic part below the sonic line. When the subsonic region of the boundary layer becomes large, which means that the sonic line is noticeably lifted off the wall (approximately for
![]() $M_{\infty }\lessapprox 1.8$
, cf. Spina et al. (Reference Spina, Smits and Robinson1994)), the APG causes the boundary-layer thickness to increase and the wall shear stress to decrease. As given in table 3(a), the usable region of the
$M_{\infty }\lessapprox 1.8$
, cf. Spina et al. (Reference Spina, Smits and Robinson1994)), the APG causes the boundary-layer thickness to increase and the wall shear stress to decrease. As given in table 3(a), the usable region of the
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.42}$
and
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.42}$
and
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}$
cases covers Mach-number ranges of
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}$
cases covers Mach-number ranges of
![]() $1.82\geqslant M_{e}\geqslant 1.50$
and
$1.82\geqslant M_{e}\geqslant 1.50$
and
![]() $1.74\geqslant M_{e}\geqslant 1.33$
, respectively, which approximately confirms the Spina et al.’s (Reference Spina, Smits and Robinson1994) switch-over value of
$1.74\geqslant M_{e}\geqslant 1.33$
, respectively, which approximately confirms the Spina et al.’s (Reference Spina, Smits and Robinson1994) switch-over value of
![]() $M_{\infty }\lessapprox 1.8$
. For the compressible, supersonic
$M_{\infty }\lessapprox 1.8$
. For the compressible, supersonic
![]() $cFPG_{\unicode[STIX]{x1D6FD}_{K}=-0.18}$
case, the supersonic part dominates the boundary layer, which thus is thickened up in its spatial development compared to the
$cFPG_{\unicode[STIX]{x1D6FD}_{K}=-0.18}$
case, the supersonic part dominates the boundary layer, which thus is thickened up in its spatial development compared to the
![]() $cZPG$
case.
$cZPG$
case.
Discussing the momentum and displacement thickness distributions for all supersonic cases in figure 11(c) next, only the ratio of the momentum thickness
![]() $\unicode[STIX]{x1D703}/\unicode[STIX]{x1D6FF}_{99}$
(symbols, left
$\unicode[STIX]{x1D703}/\unicode[STIX]{x1D6FF}_{99}$
(symbols, left
![]() $y$
-axis) is approximately constant in the streamwise direction. The ratio of the displacement thickness
$y$
-axis) is approximately constant in the streamwise direction. The ratio of the displacement thickness
![]() $\unicode[STIX]{x1D6FF}^{\ast }/\unicode[STIX]{x1D6FF}_{99}$
(lines, right
$\unicode[STIX]{x1D6FF}^{\ast }/\unicode[STIX]{x1D6FF}_{99}$
(lines, right
![]() $y$
-axis) is strongly decreased for the APG and increased for the FPG cases, approximately leading to
$y$
-axis) is strongly decreased for the APG and increased for the FPG cases, approximately leading to
![]() $\unicode[STIX]{x1D6FF}_{99}\propto \unicode[STIX]{x1D703}\not \propto \unicode[STIX]{x1D6FF}^{\ast }$
. As a consequence also the shape factor
$\unicode[STIX]{x1D6FF}_{99}\propto \unicode[STIX]{x1D703}\not \propto \unicode[STIX]{x1D6FF}^{\ast }$
. As a consequence also the shape factor
![]() $H$
is not constant anymore for the compressible results as will be further discussed in § 3.3.1. An evaluation of the kinematic boundary-layer values in figure 11(d) can reproduce almost the same trends as for the nearly incompressible cases in figure 11(b), yielding again the approximate dependency of
$H$
is not constant anymore for the compressible results as will be further discussed in § 3.3.1. An evaluation of the kinematic boundary-layer values in figure 11(d) can reproduce almost the same trends as for the nearly incompressible cases in figure 11(b), yielding again the approximate dependency of
![]() $\unicode[STIX]{x1D6FF}_{99}\propto \unicode[STIX]{x1D703}_{K}\propto \unicode[STIX]{x1D6FF}_{K}^{\ast }$
and thus the approximate constancy of
$\unicode[STIX]{x1D6FF}_{99}\propto \unicode[STIX]{x1D703}_{K}\propto \unicode[STIX]{x1D6FF}_{K}^{\ast }$
and thus the approximate constancy of
![]() $H_{K}=\unicode[STIX]{x1D6FF}_{K}^{\ast }/\unicode[STIX]{x1D703}_{K}$
.
$H_{K}=\unicode[STIX]{x1D6FF}_{K}^{\ast }/\unicode[STIX]{x1D703}_{K}$
.
3.3 Spatial evolution of averaged flow statistics
This section provides the streamwise evolution of important mean-flow parameters as a function of the local Reynolds numbers
![]() $Re_{\unicode[STIX]{x1D703}}$
or
$Re_{\unicode[STIX]{x1D703}}$
or
![]() $Re_{\unicode[STIX]{x1D70F}}$
in the same representation as for the ZPG study in Wenzel et al. (Reference Wenzel, Selent, Kloker and Rist2018b
). It should be mentioned however that the interpretation of
$Re_{\unicode[STIX]{x1D70F}}$
in the same representation as for the ZPG study in Wenzel et al. (Reference Wenzel, Selent, Kloker and Rist2018b
). It should be mentioned however that the interpretation of
![]() $Re_{\unicode[STIX]{x1D703}}$
may be difficult due to the non-intuitive development of the compressible PG TBL itself.
$Re_{\unicode[STIX]{x1D703}}$
may be difficult due to the non-intuitive development of the compressible PG TBL itself.
3.3.1 Spatial evolution of mean-flow statistics
Figures 12, 13 and 14 give the distribution of the skin-friction coefficient
![]() $c_{f}=2\overline{\unicode[STIX]{x1D70F}}_{w}/(\overline{\unicode[STIX]{x1D70C}}_{w}u_{e}^{2})$
with
$c_{f}=2\overline{\unicode[STIX]{x1D70F}}_{w}/(\overline{\unicode[STIX]{x1D70C}}_{w}u_{e}^{2})$
with
![]() $\overline{\unicode[STIX]{x1D70F}}_{w}=\overline{\unicode[STIX]{x1D707}\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}y}_{w}\approx \overline{\unicode[STIX]{x1D707}}_{w}(\unicode[STIX]{x2202}\overline{u}/\unicode[STIX]{x2202}y)_{w}$
, the skin-friction velocity Reynolds number
$\overline{\unicode[STIX]{x1D70F}}_{w}=\overline{\unicode[STIX]{x1D707}\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}y}_{w}\approx \overline{\unicode[STIX]{x1D707}}_{w}(\unicode[STIX]{x2202}\overline{u}/\unicode[STIX]{x2202}y)_{w}$
, the skin-friction velocity Reynolds number
![]() $Re_{\unicode[STIX]{x1D70F}}=\overline{\unicode[STIX]{x1D70C}}_{w}u_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D6FF}_{99}/\overline{\unicode[STIX]{x1D707}}_{w}$
and the compressible (kinematic) shape factors
$Re_{\unicode[STIX]{x1D70F}}=\overline{\unicode[STIX]{x1D70C}}_{w}u_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D6FF}_{99}/\overline{\unicode[STIX]{x1D707}}_{w}$
and the compressible (kinematic) shape factors
![]() $H_{(K)}=\unicode[STIX]{x1D6FF}_{(K)}^{\ast }/\unicode[STIX]{x1D703}_{(K)}$
as functions of the momentum-thickness Reynolds number
$H_{(K)}=\unicode[STIX]{x1D6FF}_{(K)}^{\ast }/\unicode[STIX]{x1D703}_{(K)}$
as functions of the momentum-thickness Reynolds number
![]() $Re_{\unicode[STIX]{x1D703}_{(K)}}=\unicode[STIX]{x1D70C}_{e}u_{e}\unicode[STIX]{x1D703}_{(K)}/\unicode[STIX]{x1D707}_{e}$
. Additionally, as a function of the streamwise position
$Re_{\unicode[STIX]{x1D703}_{(K)}}=\unicode[STIX]{x1D70C}_{e}u_{e}\unicode[STIX]{x1D703}_{(K)}/\unicode[STIX]{x1D707}_{e}$
. Additionally, as a function of the streamwise position
![]() $x/\unicode[STIX]{x1D6FF}_{99,0}$
and computed from
$x/\unicode[STIX]{x1D6FF}_{99,0}$
and computed from
![]() $\overline{T}_{aw}/T_{e}=1+r(\unicode[STIX]{x1D6FE}-1)/2\,M_{e}^{2}$
, the streamwise evolution of the recovery factor
$\overline{T}_{aw}/T_{e}=1+r(\unicode[STIX]{x1D6FE}-1)/2\,M_{e}^{2}$
, the streamwise evolution of the recovery factor
![]() $r$
is given in figure 15.
$r$
is given in figure 15.

Figure 12. Skin-friction coefficient
![]() $c_{f}$
as function of
$c_{f}$
as function of
![]() $Re_{\unicode[STIX]{x1D703}}$
. The incompressible, re-calibrated correlation (black solid line) is given by
$Re_{\unicode[STIX]{x1D703}}$
. The incompressible, re-calibrated correlation (black solid line) is given by
![]() $c_{f}=0.0274\,Re_{\unicode[STIX]{x1D703}}^{-0.27}$
, the compressible one by the van Driest II transformation (grey dashed lines, see White (Reference White2006)).
$c_{f}=0.0274\,Re_{\unicode[STIX]{x1D703}}^{-0.27}$
, the compressible one by the van Driest II transformation (grey dashed lines, see White (Reference White2006)).
The
![]() $c_{f}$
-distribution (figure 12) is supplemented by a black solid line representing a re-calibrated incompressible reference following
$c_{f}$
-distribution (figure 12) is supplemented by a black solid line representing a re-calibrated incompressible reference following
![]() $c_{f}=0.0274\,Re_{\unicode[STIX]{x1D703}}^{-0.27}$
(re-calibration is based on the results from Wenzel et al. (Reference Wenzel, Selent, Kloker and Rist2018b
)). Note that the re-calibrated
$c_{f}=0.0274\,Re_{\unicode[STIX]{x1D703}}^{-0.27}$
(re-calibration is based on the results from Wenzel et al. (Reference Wenzel, Selent, Kloker and Rist2018b
)). Note that the re-calibrated
![]() $c_{f}$
-correlation also better represents the Schlatter & Örlü’s (Reference Schlatter and Örlü2010) incompressible dataset. Compressible references for
$c_{f}$
-correlation also better represents the Schlatter & Örlü’s (Reference Schlatter and Örlü2010) incompressible dataset. Compressible references for
![]() $M_{\infty }=0.5$
and
$M_{\infty }=0.5$
and
![]() $2.0$
are computed from the van Driest II transformation (White Reference White2006) and are depicted as grey dashed lines; see also Wenzel et al. (Reference Wenzel, Selent, Kloker and Rist2018b
). The
$2.0$
are computed from the van Driest II transformation (White Reference White2006) and are depicted as grey dashed lines; see also Wenzel et al. (Reference Wenzel, Selent, Kloker and Rist2018b
). The
![]() $Re_{\unicode[STIX]{x1D70F}}$
- and
$Re_{\unicode[STIX]{x1D70F}}$
- and
![]() $H_{K}$
-distributions are supplemented by the incompressible references according to Schlatter & Örlü (Reference Schlatter and Örlü2010) and Chauhan, Monkewitz & Nagib (Reference Chauhan, Monkewitz and Nagib2009). Represented as grey dashed lines in figures 13 and 14, the compressible references are gained by shifting the incompressible correlations to fit the compressible ZPG results.
$H_{K}$
-distributions are supplemented by the incompressible references according to Schlatter & Örlü (Reference Schlatter and Örlü2010) and Chauhan, Monkewitz & Nagib (Reference Chauhan, Monkewitz and Nagib2009). Represented as grey dashed lines in figures 13 and 14, the compressible references are gained by shifting the incompressible correlations to fit the compressible ZPG results.

Figure 13. Skin-friction velocity Reynolds number
![]() $Re_{\unicode[STIX]{x1D70F}}$
as function of
$Re_{\unicode[STIX]{x1D70F}}$
as function of
![]() $Re_{\unicode[STIX]{x1D703}}$
. The incompressible correlation is given by
$Re_{\unicode[STIX]{x1D703}}$
. The incompressible correlation is given by
![]() $Re_{\unicode[STIX]{x1D70F}}=1.13\,Re_{\unicode[STIX]{x1D703}}^{0.843}$
(black solid line, see Schlatter & Örlü (Reference Schlatter and Örlü2010)), the compressible ones by the simple shift of the incompressible correlation (grey dashed lines).
$Re_{\unicode[STIX]{x1D70F}}=1.13\,Re_{\unicode[STIX]{x1D703}}^{0.843}$
(black solid line, see Schlatter & Örlü (Reference Schlatter and Örlü2010)), the compressible ones by the simple shift of the incompressible correlation (grey dashed lines).

Figure 14. (a) Shape factor
![]() $H$
and (b) kinematic shape factor
$H$
and (b) kinematic shape factor
![]() $H_{K}$
as a function of
$H_{K}$
as a function of
![]() $Re_{\unicode[STIX]{x1D703}}$
and
$Re_{\unicode[STIX]{x1D703}}$
and
![]() $Re_{\unicode[STIX]{x1D703},K}$
, respectively. The incompressible correlation is given as the shape of the integrated incompressible composite profiles (Chauhan et al.
Reference Chauhan, Monkewitz and Nagib2009). The compressible references are gained by a simple shift of the incompressible correlation.
$Re_{\unicode[STIX]{x1D703},K}$
, respectively. The incompressible correlation is given as the shape of the integrated incompressible composite profiles (Chauhan et al.
Reference Chauhan, Monkewitz and Nagib2009). The compressible references are gained by a simple shift of the incompressible correlation.
For the
![]() $c_{f}$
-distributions in figure 12, both the sub- and the supersonic ZPG cases show excellent agreement with the compressibility transformed re-calibrated
$c_{f}$
-distributions in figure 12, both the sub- and the supersonic ZPG cases show excellent agreement with the compressibility transformed re-calibrated
![]() $c_{f}$
-correlation. In accordance to the literature database, the
$c_{f}$
-correlation. In accordance to the literature database, the
![]() $c_{f}$
-distributions of the subsonic APG cases are shifted towards lower values for increasing APG strength. However, they almost follow the same slope as the subsonic ZPG case due to their (approximate) state of self-similarity. A comparison between the
$c_{f}$
-distributions of the subsonic APG cases are shifted towards lower values for increasing APG strength. However, they almost follow the same slope as the subsonic ZPG case due to their (approximate) state of self-similarity. A comparison between the
![]() $iAPG_{\unicode[STIX]{x1D6FD}_{K}=1.05}$
case and the incompressible
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=1.05}$
case and the incompressible
![]() $\unicode[STIX]{x1D6FD}_{K}=1.00$
case of Kitsios et al. (Reference Kitsios, Sekimoto, Atkinson, Sillero, Borrell, Gungor, Jiménez and Soria2017) (red circles) shows good agreement. The supersonic APG cases are difficult to interpret due to the strong coupling of PG and compressibility effects. According to Spina et al. (Reference Spina, Smits and Robinson1994), the wall shear stress increases monotonically through the region of applied APGs for supersonic flows where the sonic line is close to the wall, meaning that
$\unicode[STIX]{x1D6FD}_{K}=1.00$
case of Kitsios et al. (Reference Kitsios, Sekimoto, Atkinson, Sillero, Borrell, Gungor, Jiménez and Soria2017) (red circles) shows good agreement. The supersonic APG cases are difficult to interpret due to the strong coupling of PG and compressibility effects. According to Spina et al. (Reference Spina, Smits and Robinson1994), the wall shear stress increases monotonically through the region of applied APGs for supersonic flows where the sonic line is close to the wall, meaning that
![]() $M_{e}\gtrsim 1.8$
. The
$M_{e}\gtrsim 1.8$
. The
![]() $c_{f}$
-distribution, however, remains nearly constant due to the increase in
$c_{f}$
-distribution, however, remains nearly constant due to the increase in
![]() $\unicode[STIX]{x1D70C}_{e}u_{e}^{2}$
. All supersonic APG cases are therefore in a comparable
$\unicode[STIX]{x1D70C}_{e}u_{e}^{2}$
. All supersonic APG cases are therefore in a comparable
![]() $c_{f}$
-range for
$c_{f}$
-range for
![]() $Re_{\unicode[STIX]{x1D703}}\lesssim 1700$
where local Mach numbers are about
$Re_{\unicode[STIX]{x1D703}}\lesssim 1700$
where local Mach numbers are about
![]() $M_{e}\approx 1.8$
, see table 3(a). For higher Reynolds numbers, compressibility effects become weaker due to a decrease of the local Mach number and the
$M_{e}\approx 1.8$
, see table 3(a). For higher Reynolds numbers, compressibility effects become weaker due to a decrease of the local Mach number and the
![]() $c_{f}$
-distributions are increasingly dominated by PG effects. Since the PG is stronger for the
$c_{f}$
-distributions are increasingly dominated by PG effects. Since the PG is stronger for the
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}$
case compared to the
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}$
case compared to the
![]() $cAPG_{\unicode[STIX]{x1D6FD}=0.42}$
case, for instance, the
$cAPG_{\unicode[STIX]{x1D6FD}=0.42}$
case, for instance, the
![]() $c_{f}$
-distribution of the
$c_{f}$
-distribution of the
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}$
case is lower compared to the
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}$
case is lower compared to the
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.42}$
case. The interpretation of the supersonic FPG is opposite: compressibility effects (decreasing
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.42}$
case. The interpretation of the supersonic FPG is opposite: compressibility effects (decreasing
![]() $c_{f}$
) dominate the PG effect (increasing
$c_{f}$
) dominate the PG effect (increasing
![]() $c_{f}$
), which thus yields a steeper downwards running
$c_{f}$
), which thus yields a steeper downwards running
![]() $c_{f}$
-slope compared to the ZPG case.
$c_{f}$
-slope compared to the ZPG case.
The interpretation of the
![]() $Re_{\unicode[STIX]{x1D70F}}$
-distributions in figure 13 follows the same arguments as for the
$Re_{\unicode[STIX]{x1D70F}}$
-distributions in figure 13 follows the same arguments as for the
![]() $c_{f}$
-distribution due to their mutual dependency on the non-dimensional wall shear stress. Subsonic APG cases can be gained by shifting the ZPG results to higher
$c_{f}$
-distribution due to their mutual dependency on the non-dimensional wall shear stress. Subsonic APG cases can be gained by shifting the ZPG results to higher
![]() $Re_{\unicode[STIX]{x1D703}}$
- and slightly increased
$Re_{\unicode[STIX]{x1D703}}$
- and slightly increased
![]() $Re_{\unicode[STIX]{x1D70F}}$
-values. The supersonic APG and FPG cases show a consistent behaviour as the
$Re_{\unicode[STIX]{x1D70F}}$
-values. The supersonic APG and FPG cases show a consistent behaviour as the
![]() $c_{f}$
-distributions discussed before. Note that the
$c_{f}$
-distributions discussed before. Note that the
![]() $Re_{\unicode[STIX]{x1D70F}}$
-distributions for the supersonic APG cases are slightly curved in the double-logarithmic representation since they have to converge towards the incompressible distributions when decelerated to almost incompressible Mach numbers.
$Re_{\unicode[STIX]{x1D70F}}$
-distributions for the supersonic APG cases are slightly curved in the double-logarithmic representation since they have to converge towards the incompressible distributions when decelerated to almost incompressible Mach numbers.
Calculated in its compressible formulation, the shape-factor distribution
![]() $H$
(figure 14
a) is more influenced by compressibility effects than by PG effects, which makes the interpretation of the compressible results more unambiguous. Whereas the subsonic APG cases again seem to be obtainable by shifting the ZPG distribution towards higher values, the shape factors of the supersonic APG cases become significantly smaller in the streamwise direction caused by the substantial decrease in the local Mach number. For instance, the Mach number of the
$H$
(figure 14
a) is more influenced by compressibility effects than by PG effects, which makes the interpretation of the compressible results more unambiguous. Whereas the subsonic APG cases again seem to be obtainable by shifting the ZPG distribution towards higher values, the shape factors of the supersonic APG cases become significantly smaller in the streamwise direction caused by the substantial decrease in the local Mach number. For instance, the Mach number of the
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}$
case is lower at the end of the simulation domain than the Mach number of the
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}$
case is lower at the end of the simulation domain than the Mach number of the
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.55}$
case, and its shape factor is lower. For the supersonic FPG case, the reversed argument holds. When calculated without taking density variations in the wall-normal direction into account, compressibility influences are almost eliminated for the kinematic shape-factor distributions
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.55}$
case, and its shape factor is lower. For the supersonic FPG case, the reversed argument holds. When calculated without taking density variations in the wall-normal direction into account, compressibility influences are almost eliminated for the kinematic shape-factor distributions
![]() $H_{K}$
in figure 14(b). However, a quantitative comparison between sub- and supersonic cases seems not to be reasonable, see also figure 11(d). But especially for the self-similarity analysis in Gibis et al. (Reference Gibis, Wenzel, Kloker and Rist2019), the coalescence of sub- and supersonic kinematic shape factors will be utilized in the definition of appropriate length scales defining the state of the compressible PG TBL.
$H_{K}$
in figure 14(b). However, a quantitative comparison between sub- and supersonic cases seems not to be reasonable, see also figure 11(d). But especially for the self-similarity analysis in Gibis et al. (Reference Gibis, Wenzel, Kloker and Rist2019), the coalescence of sub- and supersonic kinematic shape factors will be utilized in the definition of appropriate length scales defining the state of the compressible PG TBL.

Figure 15. Distribution of the recovery factor
![]() $r$
as function of streamwise position
$r$
as function of streamwise position
![]() $x/\unicode[STIX]{x1D6FF}_{99,0}$
. Red coloured lines represent the subsonic cases, blue and cyan lines the supersonic cases. Grey dotted lines denote the induction regions where
$x/\unicode[STIX]{x1D6FF}_{99,0}$
. Red coloured lines represent the subsonic cases, blue and cyan lines the supersonic cases. Grey dotted lines denote the induction regions where
![]() $\unicode[STIX]{x1D6FD}_{(K)}$
is not yet constant, see figure 10.
$\unicode[STIX]{x1D6FD}_{(K)}$
is not yet constant, see figure 10.
The recovery factor
![]() $r$
is expected to be constant in the streamwise direction for self-similar flows, see Gibis et al. (Reference Gibis, Wenzel, Kloker and Rist2019), but not necessarily with the same value for different
$r$
is expected to be constant in the streamwise direction for self-similar flows, see Gibis et al. (Reference Gibis, Wenzel, Kloker and Rist2019), but not necessarily with the same value for different
![]() $\unicode[STIX]{x1D6FD}_{K}$
-cases. Figure 15 shows the various curves compared to the often used ZPG reference value
$\unicode[STIX]{x1D6FD}_{K}$
-cases. Figure 15 shows the various curves compared to the often used ZPG reference value
![]() $r=Pr^{1/3}\approx 0.892$
; constancy of
$r=Pr^{1/3}\approx 0.892$
; constancy of
![]() $r$
might be interpreted as an indicator for the state of self-similarity reached by the thermal boundary layer.
$r$
might be interpreted as an indicator for the state of self-similarity reached by the thermal boundary layer.
For the subsonic cases, an increasing APG means lower recovery factor values, with slightly rising trends in the streamwise direction. Whereas its value is approximately equal to
![]() $r\approx 0.88$
for the
$r\approx 0.88$
for the
![]() $iZPG$
case, its value is about
$iZPG$
case, its value is about
![]() $r\approx 0.82$
for the strongest APG case and thus decreased by 7 %. Note that the calculation of
$r\approx 0.82$
for the strongest APG case and thus decreased by 7 %. Note that the calculation of
![]() $r$
for low Mach numbers gets very sensitive and does not make sense for zero Mach number.
$r$
for low Mach numbers gets very sensitive and does not make sense for zero Mach number.
Although being much less influenced by PGs compared to the subsonic cases, similar behaviour is observed for the supersonic cases. Whereas
![]() $r$
is decreased by approximately 2 % for the strongest supersonic APG case compared to the ZPG case, the FPG case value is increased by approximately 1 %. Compared to the subsonic cases,
$r$
is decreased by approximately 2 % for the strongest supersonic APG case compared to the ZPG case, the FPG case value is increased by approximately 1 %. Compared to the subsonic cases,
![]() $r$
is much more constant in the streamwise direction for
$r$
is much more constant in the streamwise direction for
![]() $x/\unicode[STIX]{x1D6FF}_{99,0}\gtrapprox 300$
, but needs an induction distance of approximately
$x/\unicode[STIX]{x1D6FF}_{99,0}\gtrapprox 300$
, but needs an induction distance of approximately
![]() $\unicode[STIX]{x0394}x/\unicode[STIX]{x1D6FF}_{99,0}\approx 100$
to reach the constant state. It is therefore expected that the thermal boundary layer requires more time/space to fully adapt to the self-similar state. The effects of the elongated induction distance on self-similarity of local mean-flow profiles are further discussed in Gibis et al. (Reference Gibis, Wenzel, Kloker and Rist2019).
$\unicode[STIX]{x0394}x/\unicode[STIX]{x1D6FF}_{99,0}\approx 100$
to reach the constant state. It is therefore expected that the thermal boundary layer requires more time/space to fully adapt to the self-similar state. The effects of the elongated induction distance on self-similarity of local mean-flow profiles are further discussed in Gibis et al. (Reference Gibis, Wenzel, Kloker and Rist2019).
3.3.2 Spatial evolution of averaged fluctuation statistics

Figure 16. Near-wall behaviour of the streamwise velocity fluctuation
![]() $u^{\prime +}=\sqrt{\overline{u^{\prime 2}}}/u_{\unicode[STIX]{x1D70F}}$
in inner scaling versus
$u^{\prime +}=\sqrt{\overline{u^{\prime 2}}}/u_{\unicode[STIX]{x1D70F}}$
in inner scaling versus
![]() $Re_{\unicode[STIX]{x1D70F}}$
(cf. Schlatter & Örlü Reference Schlatter and Örlü2010). (a) Peak value of the wall-near maximum
$Re_{\unicode[STIX]{x1D70F}}$
(cf. Schlatter & Örlü Reference Schlatter and Örlü2010). (a) Peak value of the wall-near maximum
![]() $u_{max}^{\prime +}$
, (b) the wall-normal position of the maximum
$u_{max}^{\prime +}$
, (b) the wall-normal position of the maximum
![]() $y^{+}\left(u_{max}^{\prime +}\right)$
and (c) the wall slope
$y^{+}\left(u_{max}^{\prime +}\right)$
and (c) the wall slope
![]() $(\unicode[STIX]{x2202}u^{\prime +}/\unicode[STIX]{x2202}y^{+})|_{w}$
. Black dashed lines are references for the ZPG cases taken from Wenzel et al. (Reference Wenzel, Selent, Kloker and Rist2018b
).
$(\unicode[STIX]{x2202}u^{\prime +}/\unicode[STIX]{x2202}y^{+})|_{w}$
. Black dashed lines are references for the ZPG cases taken from Wenzel et al. (Reference Wenzel, Selent, Kloker and Rist2018b
).
The peak value
![]() $u_{max}^{\prime +}$
of the Reynolds fluctuations in the streamwise direction
$u_{max}^{\prime +}$
of the Reynolds fluctuations in the streamwise direction
![]() $u^{\prime +}=\sqrt{\overline{u^{\prime 2}}}/u_{\unicode[STIX]{x1D70F}}$
and their wall-normal position
$u^{\prime +}=\sqrt{\overline{u^{\prime 2}}}/u_{\unicode[STIX]{x1D70F}}$
and their wall-normal position
![]() $y^{+}(u_{max}^{\prime +})$
are given in figure 16(a,b), respectively. The wall slope
$y^{+}(u_{max}^{\prime +})$
are given in figure 16(a,b), respectively. The wall slope
![]() $(\unicode[STIX]{x2202}u^{\prime +}/\unicode[STIX]{x2202}y^{+})|_{w}$
is given in figure 16(c). All distributions are plotted versus
$(\unicode[STIX]{x2202}u^{\prime +}/\unicode[STIX]{x2202}y^{+})|_{w}$
is given in figure 16(c). All distributions are plotted versus
![]() $Re_{\unicode[STIX]{x1D70F}}$
. In order to emphasize their spatial trends, all data (grey solid lines in the background) are approximated by a coloured linear regression. (The linear slopes are only rough approximations which are not expected to hold for higher Reynolds numbers. The supersonic cases, for instance, are decelerated to the incompressible regime and thus have to converge to the incompressible references.) Taken from Wenzel et al. (Reference Wenzel, Selent, Kloker and Rist2018b
), black dashed lines represent references for both ZPG cases.
$Re_{\unicode[STIX]{x1D70F}}$
. In order to emphasize their spatial trends, all data (grey solid lines in the background) are approximated by a coloured linear regression. (The linear slopes are only rough approximations which are not expected to hold for higher Reynolds numbers. The supersonic cases, for instance, are decelerated to the incompressible regime and thus have to converge to the incompressible references.) Taken from Wenzel et al. (Reference Wenzel, Selent, Kloker and Rist2018b
), black dashed lines represent references for both ZPG cases.
For the subsonic cases in figure 16(a) first, the peak value of the streamwise velocity fluctuation
![]() $u_{max}^{\prime +}$
is increased by up to 10 % in the investigated
$u_{max}^{\prime +}$
is increased by up to 10 % in the investigated
![]() $\unicode[STIX]{x1D6FD}_{K}$
- and
$\unicode[STIX]{x1D6FD}_{K}$
- and
![]() $Re_{\unicode[STIX]{x1D70F}}$
-range for the strongest APG case. The slope of the linear regression is slightly increased. For the supersonic APG cases this shift is larger, since both the effect of a decreasing Mach number in the streamwise direction and APGs supplement each other. With opposing argumentation, a contrary behaviour is found for the supersonic FPG case.
$Re_{\unicode[STIX]{x1D70F}}$
-range for the strongest APG case. The slope of the linear regression is slightly increased. For the supersonic APG cases this shift is larger, since both the effect of a decreasing Mach number in the streamwise direction and APGs supplement each other. With opposing argumentation, a contrary behaviour is found for the supersonic FPG case.
For the subsonic cases, the wall-normal position of the fluctuations’ maximum value
![]() $y^{+}(u_{max}^{\prime +})$
in figure 16(b) is shifted towards the wall for lower and away from the wall for higher Reynolds numbers. For increasing APG strength, the slope of the linear regressions is increased. For the supersonic PG cases, both the effects of varying Mach number in the streamwise direction and PGs are opposed to each other, which leads to comparable distributions for the
$y^{+}(u_{max}^{\prime +})$
in figure 16(b) is shifted towards the wall for lower and away from the wall for higher Reynolds numbers. For increasing APG strength, the slope of the linear regressions is increased. For the supersonic PG cases, both the effects of varying Mach number in the streamwise direction and PGs are opposed to each other, which leads to comparable distributions for the
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.55}$
and
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.55}$
and
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}$
cases for instance. Globally, the maxima are shifted away from the wall for
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}$
cases for instance. Globally, the maxima are shifted away from the wall for
![]() $Re_{\unicode[STIX]{x1D70F}}$
larger than 350.
$Re_{\unicode[STIX]{x1D70F}}$
larger than 350.
The wall slope in figure 16(c) shows a comparable behaviour for both sub- and supersonic cases, although the slopes of the supersonic cases are somewhat lower compared to the subsonic ones. More details will be discussed in the next section.
4 Results for the transformed, local flow fields
Sub- and supersonic PG cases are not necessarily assumed to directly compare since compressibility transformations – which would enable a direct quantification of PG influences by eliminating the effect of compressibility – might be often only expected to be ‘valid by definition’ for the strict case of ZPGs. To prove the applicability of both Morkovin’s scaling/hypothesis and van Driest’s transformation for CPG TBLs, their underlying assumptions are shortly introduced and evaluated in the first part of this section. On this basis, the streamwise mean-flow velocity profiles and Reynolds fluctuations are summarized for all PG cases.
4.1 Discussion of the validity of compressibility transformations
According to Morkovin (Reference Morkovin and Favre1961), the Reynolds fluctuations
![]() $\overline{u_{i}^{\prime }u_{j}^{\prime }}$
are (almost) invariant with respect to the Mach number
$\overline{u_{i}^{\prime }u_{j}^{\prime }}$
are (almost) invariant with respect to the Mach number
![]() $M$
, if scaled with the wall-normal density ratio
$M$
, if scaled with the wall-normal density ratio
![]() $\overline{\unicode[STIX]{x1D70C}}/\overline{\unicode[STIX]{x1D70C}}_{w}$
and the skin-friction velocity
$\overline{\unicode[STIX]{x1D70C}}/\overline{\unicode[STIX]{x1D70C}}_{w}$
and the skin-friction velocity
![]() $u_{\unicode[STIX]{x1D70F}}^{2}$
$u_{\unicode[STIX]{x1D70F}}^{2}$
This is generally known as Morkovin’s scaling. Depending on the particular argumentation, this scaling uses, among others, the assumption that the total stress
![]() $\overline{\unicode[STIX]{x1D70F}}_{t}=\overline{\unicode[STIX]{x1D707}}(\text{d}\overline{u}/\text{d}y)-\overline{\unicode[STIX]{x1D70C}}\overline{u^{\prime }v^{\prime }}$
is constant and equal to
$\overline{\unicode[STIX]{x1D70F}}_{t}=\overline{\unicode[STIX]{x1D707}}(\text{d}\overline{u}/\text{d}y)-\overline{\unicode[STIX]{x1D70C}}\overline{u^{\prime }v^{\prime }}$
is constant and equal to
![]() $\overline{\unicode[STIX]{x1D70F}}_{w}$
in the inner region of the boundary layer (cf. Smits & Dussauge (Reference Smits and Dussauge2006) and Cebeci & Bradshaw (Reference Cebeci and Bradshaw1984) for instance). For PG cases, however, the shear-stress distribution varies near the wall to first order by
$\overline{\unicode[STIX]{x1D70F}}_{w}$
in the inner region of the boundary layer (cf. Smits & Dussauge (Reference Smits and Dussauge2006) and Cebeci & Bradshaw (Reference Cebeci and Bradshaw1984) for instance). For PG cases, however, the shear-stress distribution varies near the wall to first order by
![]() $\overline{\unicode[STIX]{x1D70F}}_{t}\approx \overline{\unicode[STIX]{x1D70F}}_{w}+(\text{d}p_{e}/\text{d}x)y$
and thus directly connects the total shear-stress distribution to the streamwise pressure gradient (White Reference White2006; Skote et al.
Reference Skote, Henningson and Henkes1998). Nevertheless, by assuming a constant stress region within the inner 20 per cent of the boundary layer if the PG is weak, see Cebeci & Bradshaw (Reference Cebeci and Bradshaw1984), basic compressible principles like Morkovin’s scaling are often assumed to approximately hold for the compressible PG regime.
$\overline{\unicode[STIX]{x1D70F}}_{t}\approx \overline{\unicode[STIX]{x1D70F}}_{w}+(\text{d}p_{e}/\text{d}x)y$
and thus directly connects the total shear-stress distribution to the streamwise pressure gradient (White Reference White2006; Skote et al.
Reference Skote, Henningson and Henkes1998). Nevertheless, by assuming a constant stress region within the inner 20 per cent of the boundary layer if the PG is weak, see Cebeci & Bradshaw (Reference Cebeci and Bradshaw1984), basic compressible principles like Morkovin’s scaling are often assumed to approximately hold for the compressible PG regime.
Implicitly depending on Morkovin’s scaling, the derivation of van Driest’s transformation as given by
which additionally depends on the validity of the inner layer mixing length
![]() $l_{m}^{2}=-\overline{u^{\prime }v^{\prime }}/(\unicode[STIX]{x2202}\overline{u}/\unicode[STIX]{x2202}y)^{2}$
which departs in the outer layer from its inner value even for ZPG cases, see Wenzel et al. (Reference Wenzel, Selent, Kloker and Rist2018b
), for instance. Hence, in contrast to Morkovin’s scaling, the van Driest transformation is not expected to entirely eliminate compressibility effects in the outer layer at all, as the mixing length is also expected to be influenced by PGs. Following the interpretation of Cebeci & Bradshaw (Reference Cebeci and Bradshaw1984), the van Driest transformed velocity profile
$l_{m}^{2}=-\overline{u^{\prime }v^{\prime }}/(\unicode[STIX]{x2202}\overline{u}/\unicode[STIX]{x2202}y)^{2}$
which departs in the outer layer from its inner value even for ZPG cases, see Wenzel et al. (Reference Wenzel, Selent, Kloker and Rist2018b
), for instance. Hence, in contrast to Morkovin’s scaling, the van Driest transformation is not expected to entirely eliminate compressibility effects in the outer layer at all, as the mixing length is also expected to be influenced by PGs. Following the interpretation of Cebeci & Bradshaw (Reference Cebeci and Bradshaw1984), the van Driest transformed velocity profile
thus only can be interpreted as an adequate solution of compressible PG TBLs, if its parameters
![]() $C$
and
$C$
and
![]() $\unicode[STIX]{x1D6F1}$
are calibrated to the particular case by using compressible reference data. The van Driest transformation itself only gives the framework of how this solution has to look. Also, the variation of
$\unicode[STIX]{x1D6F1}$
are calibrated to the particular case by using compressible reference data. The van Driest transformation itself only gives the framework of how this solution has to look. Also, the variation of
![]() $u_{\unicode[STIX]{x1D70F}}$
,
$u_{\unicode[STIX]{x1D70F}}$
,
![]() $C$
and
$C$
and
![]() $\unicode[STIX]{x1D6F1}$
in the streamwise
$\unicode[STIX]{x1D6F1}$
in the streamwise
![]() $x$
-direction will not generally correspond to any realizable incompressible boundary layer. Hence it may not be possible to choose a pressure distribution
$x$
-direction will not generally correspond to any realizable incompressible boundary layer. Hence it may not be possible to choose a pressure distribution
![]() $p_{e}(x)$
for an incompressible flow that will reproduce the same velocity profile as in the compressible flow at each
$p_{e}(x)$
for an incompressible flow that will reproduce the same velocity profile as in the compressible flow at each
![]() $x$
-position. Cebeci & Bradshaw (Reference Cebeci and Bradshaw1984) therefore concluded that only ‘the spirit of van Driest’s transformation, although not in its details, would be retained if compressible boundary layers were calculated using the mixing-length formula’.
$x$
-position. Cebeci & Bradshaw (Reference Cebeci and Bradshaw1984) therefore concluded that only ‘the spirit of van Driest’s transformation, although not in its details, would be retained if compressible boundary layers were calculated using the mixing-length formula’.
In the following, mainly the plausibility of Morkovin’s scaling – and thus implicitly the plausibility of van Driest’s transformation in the inner region – is discussed by evaluation of the mean shear-stress distributions. Further insight into the coupling between compressibility and PG effects are given afterwards by discussing the wall-normal distributions of the mean-flow pressure and pressure-fluctuation fields.
4.1.1 Shear-stress distributions
According to Guarini et al. (Reference Guarini, Moser, Shariff and Wray2000), the total shear stress
![]() $\overline{\unicode[STIX]{x1D70F}}_{t}$
writes
$\overline{\unicode[STIX]{x1D70F}}_{t}$
writes
 $$\begin{eqnarray}\underbrace{\overline{\unicode[STIX]{x1D70F}}_{t}}_{total\,stress}=\underbrace{\overline{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\overline{u}}{\unicode[STIX]{x2202}y}}_{mean\,stress}-\underbrace{\overline{\unicode[STIX]{x1D70C}u^{\prime \prime }v^{\prime \prime }}}_{turbulent\,stress}+\underbrace{\overline{\unicode[STIX]{x1D707}^{\prime }\left(\frac{\unicode[STIX]{x2202}u^{\prime }}{\unicode[STIX]{x2202}y}+\frac{\unicode[STIX]{x2202}v^{\prime }}{\unicode[STIX]{x2202}x}\right)}}_{stress\,correlation},\end{eqnarray}$$
$$\begin{eqnarray}\underbrace{\overline{\unicode[STIX]{x1D70F}}_{t}}_{total\,stress}=\underbrace{\overline{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\overline{u}}{\unicode[STIX]{x2202}y}}_{mean\,stress}-\underbrace{\overline{\unicode[STIX]{x1D70C}u^{\prime \prime }v^{\prime \prime }}}_{turbulent\,stress}+\underbrace{\overline{\unicode[STIX]{x1D707}^{\prime }\left(\frac{\unicode[STIX]{x2202}u^{\prime }}{\unicode[STIX]{x2202}y}+\frac{\unicode[STIX]{x2202}v^{\prime }}{\unicode[STIX]{x2202}x}\right)}}_{stress\,correlation},\end{eqnarray}$$
where
![]() $f^{\prime \prime }$
denotes fluctuations about the Favre average
$f^{\prime \prime }$
denotes fluctuations about the Favre average
![]() $\tilde{f}=\overline{\unicode[STIX]{x1D70C}f}/\overline{\unicode[STIX]{x1D70C}}$
for an unsteady quantity
$\tilde{f}=\overline{\unicode[STIX]{x1D70C}f}/\overline{\unicode[STIX]{x1D70C}}$
for an unsteady quantity
![]() $f$
. Normalized by the wall shear stress
$f$
. Normalized by the wall shear stress
![]() $\overline{\unicode[STIX]{x1D70F}}_{w}=\overline{\unicode[STIX]{x1D70C}}_{w}u_{\unicode[STIX]{x1D70F}}^{2}$
, the mean shear stress, the turbulent stress and the total stress are given in figure 17(a–c) for all cases, respectively. The distribution of the shear-stress correlation is almost zero and therefore not considered in the following. Based on the first-order expansion of the total shear-stress distribution
$\overline{\unicode[STIX]{x1D70F}}_{w}=\overline{\unicode[STIX]{x1D70C}}_{w}u_{\unicode[STIX]{x1D70F}}^{2}$
, the mean shear stress, the turbulent stress and the total stress are given in figure 17(a–c) for all cases, respectively. The distribution of the shear-stress correlation is almost zero and therefore not considered in the following. Based on the first-order expansion of the total shear-stress distribution
![]() $\overline{\unicode[STIX]{x1D70F}}_{t}\approx \overline{\unicode[STIX]{x1D70F}}_{w}+(\text{d}p_{e}/\text{d}x)y$
, the pressure-corrected total shear-stress distribution
$\overline{\unicode[STIX]{x1D70F}}_{t}\approx \overline{\unicode[STIX]{x1D70F}}_{w}+(\text{d}p_{e}/\text{d}x)y$
, the pressure-corrected total shear-stress distribution
![]() $\overline{\unicode[STIX]{x1D70F}}_{t,pc}=\overline{\unicode[STIX]{x1D70F}}_{t}-(\text{d}p_{e}/\text{d}x)y$
is given in figure 17(d). All data are extracted at
$\overline{\unicode[STIX]{x1D70F}}_{t,pc}=\overline{\unicode[STIX]{x1D70F}}_{t}-(\text{d}p_{e}/\text{d}x)y$
is given in figure 17(d). All data are extracted at
![]() $Re_{\unicode[STIX]{x1D70F}}=490$
except for the supersonic FPG case where data are extracted at
$Re_{\unicode[STIX]{x1D70F}}=490$
except for the supersonic FPG case where data are extracted at
![]() $Re_{\unicode[STIX]{x1D70F}}=360$
.
$Re_{\unicode[STIX]{x1D70F}}=360$
.

Figure 17. Comparison of (a) the mean shear stress
![]() $\overline{\unicode[STIX]{x1D707}}(\unicode[STIX]{x2202}\overline{u}/\unicode[STIX]{x2202}y)/\overline{\unicode[STIX]{x1D70F}}_{w}$
, (b) the turbulent shear stress
$\overline{\unicode[STIX]{x1D707}}(\unicode[STIX]{x2202}\overline{u}/\unicode[STIX]{x2202}y)/\overline{\unicode[STIX]{x1D70F}}_{w}$
, (b) the turbulent shear stress
![]() $-\overline{\unicode[STIX]{x1D70C}u^{\prime \prime }v^{\prime \prime }}/\overline{\unicode[STIX]{x1D70F}}_{w}$
, (c) the total shear stress
$-\overline{\unicode[STIX]{x1D70C}u^{\prime \prime }v^{\prime \prime }}/\overline{\unicode[STIX]{x1D70F}}_{w}$
, (c) the total shear stress
![]() $\overline{\unicode[STIX]{x1D70F}}_{t}$
and (d) the pressure-corrected total shear stress
$\overline{\unicode[STIX]{x1D70F}}_{t}$
and (d) the pressure-corrected total shear stress
![]() $\overline{\unicode[STIX]{x1D70F}}_{t,pc}=\overline{\unicode[STIX]{x1D70F}}_{t}-(\text{d}p_{e}/\text{d}x)y$
. Supersonic FPG data are extracted at
$\overline{\unicode[STIX]{x1D70F}}_{t,pc}=\overline{\unicode[STIX]{x1D70F}}_{t}-(\text{d}p_{e}/\text{d}x)y$
. Supersonic FPG data are extracted at
![]() $Re_{\unicode[STIX]{x1D70F}}=390$
, other data at
$Re_{\unicode[STIX]{x1D70F}}=390$
, other data at
![]() $Re_{\unicode[STIX]{x1D70F}}=490$
. Red: ———
$Re_{\unicode[STIX]{x1D70F}}=490$
. Red: ———
![]() $iZPG$
, —— -
$iZPG$
, —— -
![]() $\cdot$
$\cdot$
![]() $iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.19}$
, — - —
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.19}$
, — - —
![]() $iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.58}$
, –
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.58}$
, –
![]() $\cdot$
–
$\cdot$
–
![]() $\cdot$
–
$\cdot$
–
![]() $iAPG_{\unicode[STIX]{x1D6FD}_{K}=1.05}$
. Blue: ———
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=1.05}$
. Blue: ———
![]() $cZPG$
, ——– –
$cZPG$
, ——– –
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.15}$
, — — -
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.15}$
, — — -
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.42}$
, – – – – –
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.42}$
, – – – – –
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.55}$
, - - - - - -
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.55}$
, - - - - - -
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}$
. Cyan:
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}$
. Cyan:
![]() $-\!-$
- - –
$-\!-$
- - –
![]() $cFPG_{\unicode[STIX]{x1D6FD}_{K}=-0.18}$
.
$cFPG_{\unicode[STIX]{x1D6FD}_{K}=-0.18}$
.
Given in figure 17(a), the mean shear-stress distribution is almost constant at the wall for all cases and only slightly influenced by both compressibility and PG effects in the buffer layer between the viscous sublayer and the log layer at
![]() $3\lessapprox y^{+}\lessapprox 50$
. For the subsonic cases, the mean shear-stress distributions are slightly decreased with increasing APG strength. The supersonic cases are almost identical since effects of decreasing Mach number (increasing) and increasing effect of APG (decreasing) cancel each other.
$3\lessapprox y^{+}\lessapprox 50$
. For the subsonic cases, the mean shear-stress distributions are slightly decreased with increasing APG strength. The supersonic cases are almost identical since effects of decreasing Mach number (increasing) and increasing effect of APG (decreasing) cancel each other.
The non-dimensional turbulent stresses
![]() $-\overline{\unicode[STIX]{x1D70C}u^{\prime \prime }v^{\prime \prime }}/\overline{\unicode[STIX]{x1D70F}}_{w}$
in figure 17(b) are strongly influenced by PG effects over the entire boundary layer for both sub- and supersonic Mach numbers. For increasing APG strength a peak rises in the outer region whereas the distributions are reduced for FPGs. In contrast to the mean-flow distributions, the turbulent stresses are also noticeably influenced in the near-wall region.
$-\overline{\unicode[STIX]{x1D70C}u^{\prime \prime }v^{\prime \prime }}/\overline{\unicode[STIX]{x1D70F}}_{w}$
in figure 17(b) are strongly influenced by PG effects over the entire boundary layer for both sub- and supersonic Mach numbers. For increasing APG strength a peak rises in the outer region whereas the distributions are reduced for FPGs. In contrast to the mean-flow distributions, the turbulent stresses are also noticeably influenced in the near-wall region.
Computed as the sum of (a) and (b), the total shear-stress distributions in figure 17(c) are constant for the sub- and supersonic ZPG cases up to approximately 30–40 wall units above the wall and virtually identical. For both the sub- and supersonic PG cases the distributions are increased with distance to the wall for APG cases (
![]() $\text{d}p/\text{d}x>0$
) and decreased for the FPG case (
$\text{d}p/\text{d}x>0$
) and decreased for the FPG case (
![]() $\text{d}p_{e}/\text{d}x<0$
) by following
$\text{d}p_{e}/\text{d}x<0$
) by following
![]() $\text{d}\overline{p}/\text{d}x=\unicode[STIX]{x2202}\overline{\unicode[STIX]{x1D70F}}_{t}/\unicode[STIX]{x2202}y$
(Smits & Dussauge Reference Smits and Dussauge2006). If the PG term
$\text{d}\overline{p}/\text{d}x=\unicode[STIX]{x2202}\overline{\unicode[STIX]{x1D70F}}_{t}/\unicode[STIX]{x2202}y$
(Smits & Dussauge Reference Smits and Dussauge2006). If the PG term
![]() $(\text{d}p_{e}/\text{d}x)y$
is subtracted from the total shear-stress distributions as given in figure 17(d), the constant stress region near the wall is regained for all PG cases. Since the mean shear stresses in (a) are almost unaffected by PGs and almost constant at the wall, PG effects included in the total shear-stress distributions by
$(\text{d}p_{e}/\text{d}x)y$
is subtracted from the total shear-stress distributions as given in figure 17(d), the constant stress region near the wall is regained for all PG cases. Since the mean shear stresses in (a) are almost unaffected by PGs and almost constant at the wall, PG effects included in the total shear-stress distributions by
![]() $(\text{d}p_{e}/\text{d}x)y$
are mainly balanced by the turbulent stresses at the wall (Smits & Dussauge Reference Smits and Dussauge2006).
$(\text{d}p_{e}/\text{d}x)y$
are mainly balanced by the turbulent stresses at the wall (Smits & Dussauge Reference Smits and Dussauge2006).
A comparison between the total shear-stress distributions for the sub- and supersonic PG cases in (c) shows an almost complete agreement between the
![]() $iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.19}$
and
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.19}$
and
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.15}$
cases and the
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.15}$
cases and the
![]() $iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.58}$
and
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.58}$
and
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.55}$
cases. If incompressible and compressible PG cases are chosen to be characterized by the same kinematic Rotta–Clauser parameter
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.55}$
cases. If incompressible and compressible PG cases are chosen to be characterized by the same kinematic Rotta–Clauser parameter
![]() $\unicode[STIX]{x1D6FD}_{K}$
, cases are thus constructed with the same total shear-stress distributions. This in turn implies the Mach-number invariance of
$\unicode[STIX]{x1D6FD}_{K}$
, cases are thus constructed with the same total shear-stress distributions. This in turn implies the Mach-number invariance of
![]() $\overline{\unicode[STIX]{x1D70F}}_{t}/\overline{\unicode[STIX]{x1D70F}}_{w}$
for compressible PG cases,
$\overline{\unicode[STIX]{x1D70F}}_{t}/\overline{\unicode[STIX]{x1D70F}}_{w}$
for compressible PG cases,
As long as differences in the mean shear-stress distributions are not too large, also the turbulent stresses
![]() $-\overline{\unicode[STIX]{x1D70C}u^{\prime \prime }v^{\prime \prime }}/\overline{\unicode[STIX]{x1D70F}}_{w}$
are invariant to the Mach number, which further verifies the applicability of Morkovin’s scaling for the present compressible PG cases
$-\overline{\unicode[STIX]{x1D70C}u^{\prime \prime }v^{\prime \prime }}/\overline{\unicode[STIX]{x1D70F}}_{w}$
are invariant to the Mach number, which further verifies the applicability of Morkovin’s scaling for the present compressible PG cases
4.1.2 Pressure distributions
From the shear-stress distributions discussed in the previous section, compressibility and PG effects have been found to be almost uncoupled for the
![]() $-\overline{u^{\prime }v^{\prime }}$
fluctuations. If it is further assumed that Morkovin’s scaling also holds for the
$-\overline{u^{\prime }v^{\prime }}$
fluctuations. If it is further assumed that Morkovin’s scaling also holds for the
![]() $\overline{v^{\prime 2}}$
-fluctuations, meaning that
$\overline{v^{\prime 2}}$
-fluctuations, meaning that
![]() $(\overline{\unicode[STIX]{x1D70C}}/\overline{\unicode[STIX]{x1D70C}}_{w})(\overline{v^{\prime 2}}/u_{\unicode[STIX]{x1D70F}}^{2})\neq f(M)$
, the non-dimensionalized
$(\overline{\unicode[STIX]{x1D70C}}/\overline{\unicode[STIX]{x1D70C}}_{w})(\overline{v^{\prime 2}}/u_{\unicode[STIX]{x1D70F}}^{2})\neq f(M)$
, the non-dimensionalized
![]() $y$
-momentum equation of the two-dimensional turbulent boundary-layer equations
$y$
-momentum equation of the two-dimensional turbulent boundary-layer equations
implies that the pressure distributions
![]() $(p_{e\approx w}-\overline{p})/(\overline{\unicode[STIX]{x1D70C}}_{w}u_{\unicode[STIX]{x1D70F}}^{2})=(p_{e\approx w}-\overline{p})^{+}$
of corresponding PG cases are comparable for different Mach numbers. (The index ‘
$(p_{e\approx w}-\overline{p})/(\overline{\unicode[STIX]{x1D70C}}_{w}u_{\unicode[STIX]{x1D70F}}^{2})=(p_{e\approx w}-\overline{p})^{+}$
of corresponding PG cases are comparable for different Mach numbers. (The index ‘
![]() $e\approx w$
’ should emphasize that the pressure
$e\approx w$
’ should emphasize that the pressure
![]() $p$
can be evaluated both at the edge of the boundary layer or at the wall.) If it is also assumed that comparable mean pressure distributions yield comparable pressure fluctuations
$p$
can be evaluated both at the edge of the boundary layer or at the wall.) If it is also assumed that comparable mean pressure distributions yield comparable pressure fluctuations
![]() $p^{\prime +}=\sqrt{\overline{p^{\prime 2}}}/\overline{\unicode[STIX]{x1D70F}}_{w}$
, also their wall-normal distributions should be comparable for corresponding
$p^{\prime +}=\sqrt{\overline{p^{\prime 2}}}/\overline{\unicode[STIX]{x1D70F}}_{w}$
, also their wall-normal distributions should be comparable for corresponding
![]() $\unicode[STIX]{x1D6FD}_{K}$
-cases at different Mach numbers.
$\unicode[STIX]{x1D6FD}_{K}$
-cases at different Mach numbers.

Figure 18. (a) Mean-flow pressure distribution
![]() $(\overline{p}-\overline{p}_{w})^{+}=(\overline{p}-\overline{p}_{w})/\overline{\unicode[STIX]{x1D70F}}_{w}$
at
$(\overline{p}-\overline{p}_{w})^{+}=(\overline{p}-\overline{p}_{w})/\overline{\unicode[STIX]{x1D70F}}_{w}$
at
![]() $Re_{\unicode[STIX]{x1D70F}}=490$
and (b) pressure fluctuations
$Re_{\unicode[STIX]{x1D70F}}=490$
and (b) pressure fluctuations
![]() $p^{\prime +}=\sqrt{\overline{p^{\prime 2}}}/\overline{\unicode[STIX]{x1D70F}}_{w}$
at
$p^{\prime +}=\sqrt{\overline{p^{\prime 2}}}/\overline{\unicode[STIX]{x1D70F}}_{w}$
at
![]() $Re_{\unicode[STIX]{x1D70F}}=730$
. ZPG references: Schlatter & Örlü (Reference Schlatter and Örlü2010) at
$Re_{\unicode[STIX]{x1D70F}}=730$
. ZPG references: Schlatter & Örlü (Reference Schlatter and Örlü2010) at
![]() $Re_{\unicode[STIX]{x1D70F}}=830$
(incompressible), Pirozzoli & Bernardini (Reference Pirozzoli and Bernardini2011) at
$Re_{\unicode[STIX]{x1D70F}}=830$
(incompressible), Pirozzoli & Bernardini (Reference Pirozzoli and Bernardini2011) at
![]() $Re_{\unicode[STIX]{x1D70F}}=840$
(
$Re_{\unicode[STIX]{x1D70F}}=840$
(
![]() $M_{\infty }=2.0$
). Red: ———
$M_{\infty }=2.0$
). Red: ———
![]() $iZPG$
, —— -
$iZPG$
, —— -
![]() $\cdot$
$\cdot$
![]() $iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.19}$
, — - —
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.19}$
, — - —
![]() $iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.58}$
, –
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.58}$
, –
![]() $\cdot$
–
$\cdot$
–
![]() $\cdot$
–
$\cdot$
–
![]() $iAPG_{\unicode[STIX]{x1D6FD}_{K}=1.05}$
. Blue: ———
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=1.05}$
. Blue: ———
![]() $cZPG$
, ——– –
$cZPG$
, ——– –
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.15}$
, — — -
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.15}$
, — — -
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.42}$
, – – – – –
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.42}$
, – – – – –
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.55}$
, - - - - - -
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.55}$
, - - - - - -
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}$
. Cyan:
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}$
. Cyan:
![]() $-\!-$
- - –
$-\!-$
- - –
![]() $cFPG_{\unicode[STIX]{x1D6FD}_{K}=-0.18}$
.
$cFPG_{\unicode[STIX]{x1D6FD}_{K}=-0.18}$
.
The mean-pressure and the pressure-fluctuation distributions are depicted in figure 18(a,b), respectively. The mean-pressure fields are extracted at
![]() $Re_{\unicode[STIX]{x1D70F}}=490$
, where data of all cases except for the FPG case are available. Due to the SEM inflow boundary condition, the wall pressure fluctuations are increased by about ten per cent in the inflow region of the simulation domain for the subsonic cases. These initial disturbances have decayed after about half of the simulation domain, such that reliable pressure-fluctuation distributions are only available for the second half of the domain for the subsonic cases. The development of other flow quantities like density or temperature fluctuations are unaffected by the inflow boundary condition, see Wenzel et al. (Reference Wenzel, Selent, Kloker and Rist2018b
). For the supersonic cases, pressure fluctuations are almost immediately comparable to reference data near the inflow of the domain, as the general pressure-fluctuation level is higher inside the supersonic boundary layer. Hence, the pressure-fluctuation profiles given in figure 18(b) are extracted at
$Re_{\unicode[STIX]{x1D70F}}=490$
, where data of all cases except for the FPG case are available. Due to the SEM inflow boundary condition, the wall pressure fluctuations are increased by about ten per cent in the inflow region of the simulation domain for the subsonic cases. These initial disturbances have decayed after about half of the simulation domain, such that reliable pressure-fluctuation distributions are only available for the second half of the domain for the subsonic cases. The development of other flow quantities like density or temperature fluctuations are unaffected by the inflow boundary condition, see Wenzel et al. (Reference Wenzel, Selent, Kloker and Rist2018b
). For the supersonic cases, pressure fluctuations are almost immediately comparable to reference data near the inflow of the domain, as the general pressure-fluctuation level is higher inside the supersonic boundary layer. Hence, the pressure-fluctuation profiles given in figure 18(b) are extracted at
![]() $Re_{\unicode[STIX]{x1D70F}}=730$
to allow a meaningful comparison. Panel (b) is supplemented by incompressible and compressible ZPG reference data taken from Schlatter & Örlü (Reference Schlatter and Örlü2010) at
$Re_{\unicode[STIX]{x1D70F}}=730$
to allow a meaningful comparison. Panel (b) is supplemented by incompressible and compressible ZPG reference data taken from Schlatter & Örlü (Reference Schlatter and Örlü2010) at
![]() $Re_{\unicode[STIX]{x1D70F}}=830$
, and Pirozzoli & Bernardini (Reference Pirozzoli and Bernardini2011) at
$Re_{\unicode[STIX]{x1D70F}}=830$
, and Pirozzoli & Bernardini (Reference Pirozzoli and Bernardini2011) at
![]() $Re_{\unicode[STIX]{x1D70F}}=840$
and
$Re_{\unicode[STIX]{x1D70F}}=840$
and
![]() $M_{\infty }=2.0$
, respectively.
$M_{\infty }=2.0$
, respectively.
For increasing APG strength, the peak of the mean pressure distributions is lifted away from the wall and the profiles become fuller, see (a). The distribution of the subsonic ZPG case is slightly lower compared to the supersonic ZPG case. If evaluated at comparable
![]() $\unicode[STIX]{x1D6FD}_{K}$
-values, the distributions are almost identical for the sub- and supersonic APG cases as emphasized by the grey shaded regions. The pressure fluctuations in (b) are virtually unaffected by compressibility effects for the ZPG cases as already shown in Wenzel et al. (Reference Wenzel, Selent, Kloker and Rist2018b
) for instance, yielding an excellent agreement of the subsonic ZPG case and the incompressible and compressible ZPG references. With increasing APG strength, the fluctuation intensity increases for both sub- and supersonic cases but still remains almost identical for cases of comparable
$\unicode[STIX]{x1D6FD}_{K}$
-values, the distributions are almost identical for the sub- and supersonic APG cases as emphasized by the grey shaded regions. The pressure fluctuations in (b) are virtually unaffected by compressibility effects for the ZPG cases as already shown in Wenzel et al. (Reference Wenzel, Selent, Kloker and Rist2018b
) for instance, yielding an excellent agreement of the subsonic ZPG case and the incompressible and compressible ZPG references. With increasing APG strength, the fluctuation intensity increases for both sub- and supersonic cases but still remains almost identical for cases of comparable
![]() $\unicode[STIX]{x1D6FD}_{K}$
, yielding
$\unicode[STIX]{x1D6FD}_{K}$
, yielding
4.1.3 Wall-normal velocity fluctuations
 $\overline{v^{\prime 2}}$
$\overline{v^{\prime 2}}$
Based on the previous argumentation, the close agreement between the mean-pressure distributions of sub- and supersonic counterparts with similar
![]() $\unicode[STIX]{x1D6FD}_{K}$
has been implied by the assumed validity of Morkovin’s scaling for the wall-normal velocity fluctuations
$\unicode[STIX]{x1D6FD}_{K}$
has been implied by the assumed validity of Morkovin’s scaling for the wall-normal velocity fluctuations
![]() $\overline{v^{\prime 2}}$
(or vice versa). To verify the accuracy of the simplified
$\overline{v^{\prime 2}}$
(or vice versa). To verify the accuracy of the simplified
![]() $y$
-momentum equation of the turbulent boundary-layer equations for compressible PG cases (4.7) and thus the success of Morkovin’s scaling for the wall-normal velocity fluctuations
$y$
-momentum equation of the turbulent boundary-layer equations for compressible PG cases (4.7) and thus the success of Morkovin’s scaling for the wall-normal velocity fluctuations
![]() $\overline{v^{\prime 2}}$
, these are given both in unscaled
$\overline{v^{\prime 2}}$
, these are given both in unscaled
![]() $\sqrt{\overline{v^{\prime 2}}}/u_{\unicode[STIX]{x1D70F}}$
and Morkovin-scaled
$\sqrt{\overline{v^{\prime 2}}}/u_{\unicode[STIX]{x1D70F}}$
and Morkovin-scaled
![]() $\sqrt{\overline{\unicode[STIX]{x1D70C}}/\overline{\unicode[STIX]{x1D70C}}_{w}}\sqrt{\overline{v^{\prime 2}}}/u_{\unicode[STIX]{x1D70F}}$
representation in figure 19(a,b), respectively. For better comparability, only sub- and supersonic cases with similar
$\sqrt{\overline{\unicode[STIX]{x1D70C}}/\overline{\unicode[STIX]{x1D70C}}_{w}}\sqrt{\overline{v^{\prime 2}}}/u_{\unicode[STIX]{x1D70F}}$
representation in figure 19(a,b), respectively. For better comparability, only sub- and supersonic cases with similar
![]() $\unicode[STIX]{x1D6FD}_{K}$
-values are considered. All results are extracted at the three Reynolds-number values
$\unicode[STIX]{x1D6FD}_{K}$
-values are considered. All results are extracted at the three Reynolds-number values
![]() $Re_{\unicode[STIX]{x1D70F}}=490$
, 610 and 730, diagonally staggered in ascending order. Represented as circled symbols in (b), some pressure distributions
$Re_{\unicode[STIX]{x1D70F}}=490$
, 610 and 730, diagonally staggered in ascending order. Represented as circled symbols in (b), some pressure distributions
![]() $\sqrt{(\overline{p}_{w}-\overline{p})/(\overline{\unicode[STIX]{x1D70C}}_{w}u_{\unicode[STIX]{x1D70F}}^{2})}$
are additionally given for selected cases.
$\sqrt{(\overline{p}_{w}-\overline{p})/(\overline{\unicode[STIX]{x1D70C}}_{w}u_{\unicode[STIX]{x1D70F}}^{2})}$
are additionally given for selected cases.

Figure 19. Comparison of wall-normal Reynolds fluctuations at
![]() $Re_{\unicode[STIX]{x1D70F}}=490$
, 610 and 730 in (a) unscaled formulation
$Re_{\unicode[STIX]{x1D70F}}=490$
, 610 and 730 in (a) unscaled formulation
![]() $v^{\prime +}=\sqrt{\overline{v^{\prime 2}}}/u_{\unicode[STIX]{x1D70F}}$
and (b) density-scaled formulation
$v^{\prime +}=\sqrt{\overline{v^{\prime 2}}}/u_{\unicode[STIX]{x1D70F}}$
and (b) density-scaled formulation
![]() $v_{M}^{\prime +}=\sqrt{\overline{\unicode[STIX]{x1D70C}}/\overline{\unicode[STIX]{x1D70C}}_{w}}\sqrt{v^{\prime 2}}/u_{\unicode[STIX]{x1D70F}}$
as lines. Filled square symbols in (b) represent the pressure distribution
$v_{M}^{\prime +}=\sqrt{\overline{\unicode[STIX]{x1D70C}}/\overline{\unicode[STIX]{x1D70C}}_{w}}\sqrt{v^{\prime 2}}/u_{\unicode[STIX]{x1D70F}}$
as lines. Filled square symbols in (b) represent the pressure distribution
![]() $\sqrt{\overline{p}_{w}-\overline{p}}/(\sqrt{\overline{\unicode[STIX]{x1D70C}}_{w}}u_{\unicode[STIX]{x1D70F}})$
as already given in figure 18(a). Only corresponding cases of comparable
$\sqrt{\overline{p}_{w}-\overline{p}}/(\sqrt{\overline{\unicode[STIX]{x1D70C}}_{w}}u_{\unicode[STIX]{x1D70F}})$
as already given in figure 18(a). Only corresponding cases of comparable
![]() $\unicode[STIX]{x1D6FD}_{K}$
-values are given. All red: ———
$\unicode[STIX]{x1D6FD}_{K}$
-values are given. All red: ———
![]() $iZPG$
, —— -
$iZPG$
, —— -
![]() $\cdot$
$\cdot$
![]() $iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.19}$
, — - —
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.19}$
, — - —
![]() $iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.58}$
. All blue: ———
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.58}$
. All blue: ———
![]() $cZPG$
, ——– –
$cZPG$
, ——– –
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.15}$
, – – – – –
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.15}$
, – – – – –
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.55}$
.
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.55}$
.
If the pressure distributions and the corresponding Morkovin-scaled velocity fluctuations are compared in (b) first, an almost complete agreement can be established up to the boundary-layer edge
![]() $\unicode[STIX]{x1D6FF}_{99}^{+}=Re_{\unicode[STIX]{x1D70F}}$
. Thus, both the validity of (4.7) for compressible PG cases with similar
$\unicode[STIX]{x1D6FF}_{99}^{+}=Re_{\unicode[STIX]{x1D70F}}$
. Thus, both the validity of (4.7) for compressible PG cases with similar
![]() $\unicode[STIX]{x1D6FD}_{K}$
-values and the approximate validity of Morkovin’s scaling for the wall-normal velocity fluctuations
$\unicode[STIX]{x1D6FD}_{K}$
-values and the approximate validity of Morkovin’s scaling for the wall-normal velocity fluctuations
![]() $\overline{v^{\prime 2}}$
are implied. If assessed against the untransformed distributions in (a), no complete scaling success can be found for the ZPG cases. While the incompressible distribution is noticeably above the compressible one in the unscaled representation in (a), the incompressible one is noticeably below the compressible one in the density-scaled representation in (b), see also Wenzel et al. (Reference Wenzel, Selent, Kloker and Rist2018b
). In contrast, the scaling success is better for the APG cases, mainly caused by the smaller Mach numbers of the APG cases at the given Reynolds numbers.
$\overline{v^{\prime 2}}$
are implied. If assessed against the untransformed distributions in (a), no complete scaling success can be found for the ZPG cases. While the incompressible distribution is noticeably above the compressible one in the unscaled representation in (a), the incompressible one is noticeably below the compressible one in the density-scaled representation in (b), see also Wenzel et al. (Reference Wenzel, Selent, Kloker and Rist2018b
). In contrast, the scaling success is better for the APG cases, mainly caused by the smaller Mach numbers of the APG cases at the given Reynolds numbers.
4.2 Local mean-flow statistics
In the previous section both the non-dimensional turbulent stresses
![]() $-\overline{\unicode[STIX]{x1D70C}u^{\prime }v^{\prime }}/\overline{\unicode[STIX]{x1D70F}}_{w}$
and
$-\overline{\unicode[STIX]{x1D70C}u^{\prime }v^{\prime }}/\overline{\unicode[STIX]{x1D70F}}_{w}$
and
![]() $\overline{\unicode[STIX]{x1D70C}v^{\prime 2}}/\overline{\unicode[STIX]{x1D70F}}_{w}$
have been found to be almost unaffected by compressibility effects for PG cases with comparable
$\overline{\unicode[STIX]{x1D70C}v^{\prime 2}}/\overline{\unicode[STIX]{x1D70F}}_{w}$
have been found to be almost unaffected by compressibility effects for PG cases with comparable
![]() $\unicode[STIX]{x1D6FD}_{K}$
-values in the investigated Mach- and Reynolds-number ranges. The so confirmed validity of Morkovin’s scaling/hypothesis for the given CPG TBLs further implies the approximate validity of van Driest’s transformation in the inner region of the TBL as discussed before. In this section, both the profiles of the local mean-flow velocity
$\unicode[STIX]{x1D6FD}_{K}$
-values in the investigated Mach- and Reynolds-number ranges. The so confirmed validity of Morkovin’s scaling/hypothesis for the given CPG TBLs further implies the approximate validity of van Driest’s transformation in the inner region of the TBL as discussed before. In this section, both the profiles of the local mean-flow velocity
![]() $\overline{u}$
and the streamwise velocity fluctuations
$\overline{u}$
and the streamwise velocity fluctuations
![]() $\overline{u^{\prime 2}}$
are investigated in more detail. To this end, all results are discussed separately for the sub- and supersonic regime first in order to work out the effect of varying PGs on the respective regime.
$\overline{u^{\prime 2}}$
are investigated in more detail. To this end, all results are discussed separately for the sub- and supersonic regime first in order to work out the effect of varying PGs on the respective regime.
4.2.1 Mean-flow velocity profiles
 $\overline{u}$
$\overline{u}$
The streamwise mean-flow velocity profiles
![]() $\overline{u}^{+}$
are given in figures 20 and 21 for all sub- and supersonic cases, respectively, the inner layer on the left, the outer layer on the right. All results are extracted at the same three Reynolds numbers
$\overline{u}^{+}$
are given in figures 20 and 21 for all sub- and supersonic cases, respectively, the inner layer on the left, the outer layer on the right. All results are extracted at the same three Reynolds numbers
![]() $Re_{\unicode[STIX]{x1D70F}}=490$
,
$Re_{\unicode[STIX]{x1D70F}}=490$
,
![]() $610$
and
$610$
and
![]() $730$
if available, except for the supersonic FPG case extracted at
$730$
if available, except for the supersonic FPG case extracted at
![]() $Re_{\unicode[STIX]{x1D70F}}=360$
. All velocity profiles are located in regions of well-developed
$Re_{\unicode[STIX]{x1D70F}}=360$
. All velocity profiles are located in regions of well-developed
![]() $\unicode[STIX]{x1D6FD}_{K}$
-parameter distributions, see figure 10.
$\unicode[STIX]{x1D6FD}_{K}$
-parameter distributions, see figure 10.
In the subsonic cases (figure 20) often reported results can be seen. Whereas the velocity profiles are shifted down to lower
![]() $\overline{u}^{+}$
-values in the logarithmic region with increasing
$\overline{u}^{+}$
-values in the logarithmic region with increasing
![]() $\unicode[STIX]{x1D6FD}_{K}$
, they are lifted in the wake region. Evaluated at
$\unicode[STIX]{x1D6FD}_{K}$
, they are lifted in the wake region. Evaluated at
![]() $y^{+}\approx 50$
and
$y^{+}\approx 50$
and
![]() $y^{+}=\unicode[STIX]{x1D6FF}_{99}^{+}=Re_{\unicode[STIX]{x1D70F}}$
, this shift is almost constant for all given Reynolds numbers.
$y^{+}=\unicode[STIX]{x1D6FF}_{99}^{+}=Re_{\unicode[STIX]{x1D70F}}$
, this shift is almost constant for all given Reynolds numbers.
Mainly due to the varying effect of compressibility in the streamwise direction, the supersonic APG results as given in figure 21 are more difficult to interpret. In the logarithmic region, both the opposing effects of compressibility (lifting for decreasing streamwise Mach numbers) and APGs (shifting down for increasing APG strength) balance each other, yielding the almost same distributions in the logarithmic layer for all APG cases in figure 21(a) (cf. also figure 12 or 17
a). In the wake region where both effects constructively overlap (lifting up for increasing APG strength and decreasing streamwise Mach number),
![]() $\overline{u}^{+}$
-values are increased with increasing
$\overline{u}^{+}$
-values are increased with increasing
![]() $\unicode[STIX]{x1D6FD}_{K}$
, see
$\unicode[STIX]{x1D6FD}_{K}$
, see
![]() $y^{+}=Re_{\unicode[STIX]{x1D70F}}=\unicode[STIX]{x1D6FF}_{99}^{+}$
in figure 21(b). However, due to the decreasing influence of compressibility in the streamwise direction, this shift is not expected to be constant for increasing Reynolds numbers. An assessment of the supersonic FPG case shows inverted trends.
$y^{+}=Re_{\unicode[STIX]{x1D70F}}=\unicode[STIX]{x1D6FF}_{99}^{+}$
in figure 21(b). However, due to the decreasing influence of compressibility in the streamwise direction, this shift is not expected to be constant for increasing Reynolds numbers. An assessment of the supersonic FPG case shows inverted trends.
4.2.2 The van Driest transformation
Figures 22 and 23 illustrate the untransformed and van Driest transformed mean-flow distributions
![]() $\overline{u}^{+}$
and
$\overline{u}^{+}$
and
![]() $\overline{u}_{VD}^{+}$
(4.2), respectively, both for the subsonic
$\overline{u}_{VD}^{+}$
(4.2), respectively, both for the subsonic
![]() $iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.19}$
and
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.19}$
and
![]() $iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.58}$
cases and the compressible
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.58}$
cases and the compressible
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.15}$
and
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.15}$
and
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.55}$
cases. Based on the total shear-stress distributions
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.55}$
cases. Based on the total shear-stress distributions
![]() $\overline{\unicode[STIX]{x1D70F}}_{t}$
discussed in the previous section, the compressible cases should coincide with the incompressible ones if the van Driest transformation is successful.
$\overline{\unicode[STIX]{x1D70F}}_{t}$
discussed in the previous section, the compressible cases should coincide with the incompressible ones if the van Driest transformation is successful.

Figure 20. Comparison of subsonic mean-flow velocity profiles
![]() $\overline{u}^{+}$
at
$\overline{u}^{+}$
at
![]() $Re_{\unicode[STIX]{x1D70F}}=490$
,
$Re_{\unicode[STIX]{x1D70F}}=490$
,
![]() $610$
and
$610$
and
![]() $730$
. Black dotted lines denote the viscous sublayer
$730$
. Black dotted lines denote the viscous sublayer
![]() $\overline{u}^{+}=y^{+}$
, dashed black lines the logarithmic region
$\overline{u}^{+}=y^{+}$
, dashed black lines the logarithmic region
![]() $\overline{u}^{+}=1/k\,\ln y^{+}+C$
with
$\overline{u}^{+}=1/k\,\ln y^{+}+C$
with
![]() $k=0.41$
and
$k=0.41$
and
![]() $C=5.2$
. All red: ———
$C=5.2$
. All red: ———
![]() $iZPG$
, —— -
$iZPG$
, —— -
![]() $\cdot$
$\cdot$
![]() $iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.19}$
, — - —
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.19}$
, — - —
![]() $iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.58}$
, —— -
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.58}$
, —— -
![]() $\cdot$
$\cdot$
![]() $iAPG_{\unicode[STIX]{x1D6FD}_{K}=1.05}$
.
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=1.05}$
.

Figure 21. Comparison of supersonic mean-flow velocity profiles
![]() $\overline{u}^{+}$
at
$\overline{u}^{+}$
at
![]() $Re_{\unicode[STIX]{x1D70F}}=490$
,
$Re_{\unicode[STIX]{x1D70F}}=490$
,
![]() $610$
and
$610$
and
![]() $730$
for ZPG/APG and
$730$
for ZPG/APG and
![]() $Re_{\unicode[STIX]{x1D70F}}=360$
for FPG cases. Further information are given in figure 20. All blue: ———
$Re_{\unicode[STIX]{x1D70F}}=360$
for FPG cases. Further information are given in figure 20. All blue: ———
![]() $cZPG$
, ——– –
$cZPG$
, ——– –
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.15}$
, — — -
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.15}$
, — — -
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.42}$
, – – – – –
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.42}$
, – – – – –
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.55}$
, - - - - - -
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.55}$
, - - - - - -
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}$
. Cyan:
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}$
. Cyan:
![]() $-\!-$
- - –
$-\!-$
- - –
![]() $cFPG_{\unicode[STIX]{x1D6FD}=-0.35}$
.
$cFPG_{\unicode[STIX]{x1D6FD}=-0.35}$
.

Figure 22. Comparison of sub- and supersonic mean-flow velocity profiles
![]() $\overline{u}^{+}$
at
$\overline{u}^{+}$
at
![]() $Re_{\unicode[STIX]{x1D70F}}=490$
,
$Re_{\unicode[STIX]{x1D70F}}=490$
,
![]() $610$
and
$610$
and
![]() $730$
. Black dotted lines denote the viscous sublayer
$730$
. Black dotted lines denote the viscous sublayer
![]() $\overline{u}^{+}=y^{+}$
, dashed black lines the logarithmic region
$\overline{u}^{+}=y^{+}$
, dashed black lines the logarithmic region
![]() $\overline{u}^{+}=1/k\,\ln y^{+}+C$
with
$\overline{u}^{+}=1/k\,\ln y^{+}+C$
with
![]() $k=0.41$
and
$k=0.41$
and
![]() $C=5.2$
. Only corresponding cases of comparable
$C=5.2$
. Only corresponding cases of comparable
![]() $\unicode[STIX]{x1D6FD}_{K}$
-values are given. All red: ———
$\unicode[STIX]{x1D6FD}_{K}$
-values are given. All red: ———
![]() $iZPG$
, —— -
$iZPG$
, —— -
![]() $\cdot$
$\cdot$
![]() $iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.19}$
, — - —
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.19}$
, — - —
![]() $iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.58}$
. All blue: ———
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.58}$
. All blue: ———
![]() $cZPG$
, ——– –
$cZPG$
, ——– –
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.15}$
, - - - - - -
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.15}$
, - - - - - -
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.55}$
.
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.55}$
.

Figure 23. Same as figure 22, but for van Driest transformed profiles
![]() $\overline{u}_{VD}^{+}$
.
$\overline{u}_{VD}^{+}$
.
For the inner layer, figure 23(a), the supersonic velocity profiles
![]() $\overline{u}_{VD}^{+}$
are almost perfectly shifted into their subsonic counterparts, compare figures 22(a) and 23(a). In the wake region for
$\overline{u}_{VD}^{+}$
are almost perfectly shifted into their subsonic counterparts, compare figures 22(a) and 23(a). In the wake region for
![]() $y^{+}\gtrapprox 100$
(figure 23
b), the subsonic
$y^{+}\gtrapprox 100$
(figure 23
b), the subsonic
![]() $iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.19}$
and supersonic
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.19}$
and supersonic
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.15}$
cases are almost identical, whereas the supersonic
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.15}$
cases are almost identical, whereas the supersonic
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.55}$
case lies noticeably below the subsonic
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.55}$
case lies noticeably below the subsonic
![]() $iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.58}$
case. In the ZPG case, however, the van Driest transformed distributions lie above the incompressible references if compared at the same
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.58}$
case. In the ZPG case, however, the van Driest transformed distributions lie above the incompressible references if compared at the same
![]() $Re_{\unicode[STIX]{x1D70F}}$
, see Wenzel et al. (Reference Wenzel, Selent, Kloker and Rist2018b
). Consequently, the wake distribution of the van Driest transformed velocity profiles is increasingly underestimated with increasing APG strength. For the weak
$Re_{\unicode[STIX]{x1D70F}}$
, see Wenzel et al. (Reference Wenzel, Selent, Kloker and Rist2018b
). Consequently, the wake distribution of the van Driest transformed velocity profiles is increasingly underestimated with increasing APG strength. For the weak
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.15}$
case, the underestimating effect by the APG balances the overestimating effect by compressibility, whereas it is overcompensated for the stronger
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.15}$
case, the underestimating effect by the APG balances the overestimating effect by compressibility, whereas it is overcompensated for the stronger
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.55}$
case. Thus, with increasing
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.55}$
case. Thus, with increasing
![]() $Re_{\unicode[STIX]{x1D70F}}$
and thus decreased Mach number in APG flows, also the success of van Driest’s transformation varies. In some contrast to the ZPG study however, the van Driest transformation can be denoted to be still approximately valid for the wake region of the present PG cases, since compressibility effects are significantly reduced, although not being completely excluded.
$Re_{\unicode[STIX]{x1D70F}}$
and thus decreased Mach number in APG flows, also the success of van Driest’s transformation varies. In some contrast to the ZPG study however, the van Driest transformation can be denoted to be still approximately valid for the wake region of the present PG cases, since compressibility effects are significantly reduced, although not being completely excluded.

Figure 24. Comparison of subsonic streamwise Reynolds fluctuations
![]() $u^{\prime +}=\sqrt{\overline{u^{\prime 2}}}/u_{\unicode[STIX]{x1D70F}}$
at
$u^{\prime +}=\sqrt{\overline{u^{\prime 2}}}/u_{\unicode[STIX]{x1D70F}}$
at
![]() $Re_{\unicode[STIX]{x1D70F}}=490$
,
$Re_{\unicode[STIX]{x1D70F}}=490$
,
![]() $610$
and
$610$
and
![]() $730$
. Solid lines represent the ZPG case, non-solid lines APG cases. Arrows denote the direction of increasing APG strength
$730$
. Solid lines represent the ZPG case, non-solid lines APG cases. Arrows denote the direction of increasing APG strength
![]() $\unicode[STIX]{x1D6FD}_{K}$
. Red: ———
$\unicode[STIX]{x1D6FD}_{K}$
. Red: ———
![]() $iZPG$
, —— -
$iZPG$
, —— -
![]() $\cdot$
$\cdot$
![]() $iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.19}$
, — - —
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.19}$
, — - —
![]() $iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.58}$
, –
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.58}$
, –
![]() $\cdot$
–
$\cdot$
–
![]() $\cdot$
–
$\cdot$
–
![]() $iAPG_{\unicode[STIX]{x1D6FD}_{K}=1.05}$
.
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=1.05}$
.

Figure 25. Comparison of supersonic streamwise Reynolds fluctuations
![]() $u^{\prime +}=\sqrt{\overline{u^{\prime 2}}}/u_{\unicode[STIX]{x1D70F}}$
at
$u^{\prime +}=\sqrt{\overline{u^{\prime 2}}}/u_{\unicode[STIX]{x1D70F}}$
at
![]() $Re_{\unicode[STIX]{x1D70F}}=490$
,
$Re_{\unicode[STIX]{x1D70F}}=490$
,
![]() $610$
and
$610$
and
![]() $730$
for ZPG/APG and
$730$
for ZPG/APG and
![]() $Re_{\unicode[STIX]{x1D70F}}=360$
for FPG cases. Blue: ———
$Re_{\unicode[STIX]{x1D70F}}=360$
for FPG cases. Blue: ———
![]() $cZPG$
, ——– –
$cZPG$
, ——– –
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.15}$
, — — -
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.15}$
, — — -
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.42}$
, – – – – –
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.42}$
, – – – – –
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.55}$
, - - - - - -
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.55}$
, - - - - - -
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}$
. Cyan:
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}$
. Cyan:
![]() $-\!-$
- - –
$-\!-$
- - –
![]() $cFPG_{\unicode[STIX]{x1D6FD}=-0.35}$
.
$cFPG_{\unicode[STIX]{x1D6FD}=-0.35}$
.

Figure 26. Comparison of sub- and supersonic streamwise Reynolds fluctuations
![]() $u^{\prime +}=\sqrt{\overline{u^{\prime 2}}}/u_{\unicode[STIX]{x1D70F}}$
at
$u^{\prime +}=\sqrt{\overline{u^{\prime 2}}}/u_{\unicode[STIX]{x1D70F}}$
at
![]() $Re_{\unicode[STIX]{x1D70F}}=490$
,
$Re_{\unicode[STIX]{x1D70F}}=490$
,
![]() $610$
and
$610$
and
![]() $730$
. Only corresponding cases of comparable
$730$
. Only corresponding cases of comparable
![]() $\unicode[STIX]{x1D6FD}_{K}$
-values are given. All red: —— -
$\unicode[STIX]{x1D6FD}_{K}$
-values are given. All red: —— -
![]() $\cdot$
$\cdot$
![]() $iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.19}$
, — - —
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.19}$
, — - —
![]() $iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.58}$
. All blue: ——– –
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.58}$
. All blue: ——– –
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.15}$
, - - - - - -
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.15}$
, - - - - - -
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.55}$
.
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.55}$
.

Figure 27. Same as figure 26, but for density-scaled streamwise Reynolds fluctuations,
![]() $u_{M}^{\prime +}=\sqrt{\overline{\unicode[STIX]{x1D70C}}/\overline{\unicode[STIX]{x1D70C}}_{w}}\sqrt{\overline{u^{\prime 2}}}/u_{\unicode[STIX]{x1D70F}}$
.
$u_{M}^{\prime +}=\sqrt{\overline{\unicode[STIX]{x1D70C}}/\overline{\unicode[STIX]{x1D70C}}_{w}}\sqrt{\overline{u^{\prime 2}}}/u_{\unicode[STIX]{x1D70F}}$
.
4.2.3 Reynolds fluctuations
 $\overline{u^{\prime 2}}$
$\overline{u^{\prime 2}}$
In the same representation as for the mean velocity profiles, the streamwise Reynolds-averaged velocity fluctuations
![]() $u^{\prime +}=\sqrt{\overline{u^{\prime 2}}}/u_{\unicode[STIX]{x1D70F}}$
are given in figures 24 and 25 separately for the sub- and supersonic cases, respectively.
$u^{\prime +}=\sqrt{\overline{u^{\prime 2}}}/u_{\unicode[STIX]{x1D70F}}$
are given in figures 24 and 25 separately for the sub- and supersonic cases, respectively.
At first and in extension of figure 16, the inner layer of the Reynolds fluctuations is revisited in figures 24(a) and 25(a). In comparison to the compressible ZPG cases (Wenzel et al.
Reference Wenzel, Selent, Kloker and Rist2018b
), the Reynolds fluctuation profiles do not match for different PG cases near the wall for
![]() $y^{+}\lessapprox 10$
. The distributions are increased for APGs and decreased for FPGs causing higher and lower values for
$y^{+}\lessapprox 10$
. The distributions are increased for APGs and decreased for FPGs causing higher and lower values for
![]() $(\unicode[STIX]{x2202}u^{\prime +}/\unicode[STIX]{x2202}y^{+})|_{w}$
, respectively, see figure 16(c). The position of the near-wall fluctuation maximum is increased for APGs and decreased for FPGs as already has been seen in figure 16(a,b). However, in combination with the effect of varying Mach number in streamwise direction, the interpretation of the peak’s absolute value is again complex for the supersonic cases. Consistently given for both the sub- and supersonic cases in figures 24(b) and 25(b), the well-known second maximum appears in the outer region of the boundary layer, see Skote et al. (Reference Skote, Henningson and Henkes1998) and Kitsios et al. (Reference Kitsios, Sekimoto, Atkinson, Sillero, Borrell, Gungor, Jiménez and Soria2017), for instance.
$(\unicode[STIX]{x2202}u^{\prime +}/\unicode[STIX]{x2202}y^{+})|_{w}$
, respectively, see figure 16(c). The position of the near-wall fluctuation maximum is increased for APGs and decreased for FPGs as already has been seen in figure 16(a,b). However, in combination with the effect of varying Mach number in streamwise direction, the interpretation of the peak’s absolute value is again complex for the supersonic cases. Consistently given for both the sub- and supersonic cases in figures 24(b) and 25(b), the well-known second maximum appears in the outer region of the boundary layer, see Skote et al. (Reference Skote, Henningson and Henkes1998) and Kitsios et al. (Reference Kitsios, Sekimoto, Atkinson, Sillero, Borrell, Gungor, Jiménez and Soria2017), for instance.
4.2.4 Morkovin scaling
Both in its unscaled
![]() $u^{\prime +}=\sqrt{\overline{u^{\prime 2}}}/u_{\unicode[STIX]{x1D70F}}$
and Morkovin-scaled representation
$u^{\prime +}=\sqrt{\overline{u^{\prime 2}}}/u_{\unicode[STIX]{x1D70F}}$
and Morkovin-scaled representation
![]() $u_{M}^{\prime +}=\sqrt{\overline{\unicode[STIX]{x1D70C}}/\overline{\unicode[STIX]{x1D70C}}_{w}}\sqrt{\overline{u^{\prime 2}}}/u_{\unicode[STIX]{x1D70F}}$
, the Reynolds fluctuations are depicted in figures 26 and 27, respectively. As for the mean-flow distributions, only the subsonic
$u_{M}^{\prime +}=\sqrt{\overline{\unicode[STIX]{x1D70C}}/\overline{\unicode[STIX]{x1D70C}}_{w}}\sqrt{\overline{u^{\prime 2}}}/u_{\unicode[STIX]{x1D70F}}$
, the Reynolds fluctuations are depicted in figures 26 and 27, respectively. As for the mean-flow distributions, only the subsonic
![]() $iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.19}$
and
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.19}$
and
![]() $iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.58}$
cases and the compressible
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.58}$
cases and the compressible
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.15}$
and
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.15}$
and
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.55}$
cases are depicted, for which the PG influence is comparable.
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.55}$
cases are depicted, for which the PG influence is comparable.
If compared in the unscaled representation in figure 26, both the inner and the outer peaks of the supersonic cases are reduced compared to the subsonic results. In the Morkovin-scaled representation in figure 27, both the inner and the outer peaks of the supersonic cases are slightly lifted above the subsonic results. It is noted, however, that this behaviour has been also observed in the ZPG study to a similar extent, see Wenzel et al. (Reference Wenzel, Selent, Kloker and Rist2018b
), and is therefore much more attributed to compressibility than to PG effects. Morkovin’s scaling thus also can be confirmed for the present PG cases to a comparable extent as for the ZPG cases, which further implies the Mach-number invariance of the non-dimensionalized streamwise
![]() $\overline{\unicode[STIX]{x1D70C}u^{\prime \prime 2}}/\overline{\unicode[STIX]{x1D70F}}_{w}$
stress
$\overline{\unicode[STIX]{x1D70C}u^{\prime \prime 2}}/\overline{\unicode[STIX]{x1D70F}}_{w}$
stress
5 Conclusions
The main goal of the present study is to identify the effects of pressure gradients as uniquely as possible on compressible flat-plate turbulent boundary layers (TBLs). To this end, spatial DNS of compressible, self-similar PG TBLs have been conducted and analysed both for sub- and supersonic inflow Mach numbers for the first time. The equilibrium character of the investigated flows allows for a direct comparison of sub- and supersonic cases. It turned out that the kinematic Rotta–Clauser parameter
![]() $\unicode[STIX]{x1D6FD}_{K}$
built by the incompressible boundary-layer displacement thickness as the length scale is the right similarity parameter, see also Gibis et al. (Reference Gibis, Wenzel, Kloker and Rist2019). Thus, by regarding both incompressible and compressibility transformed compressible counterparts, the isolated effects of continuous PGs can be evaluated, and the validity of the most common compressibility transformations scrutinized.
$\unicode[STIX]{x1D6FD}_{K}$
built by the incompressible boundary-layer displacement thickness as the length scale is the right similarity parameter, see also Gibis et al. (Reference Gibis, Wenzel, Kloker and Rist2019). Thus, by regarding both incompressible and compressibility transformed compressible counterparts, the isolated effects of continuous PGs can be evaluated, and the validity of the most common compressibility transformations scrutinized.
One ZPG and three APG cases have been investigated for the subsonic regime (inflow Mach number
![]() $M_{\infty ,0}=0.5$
,
$M_{\infty ,0}=0.5$
,
![]() $\unicode[STIX]{x1D6FD}_{K}=0$
,
$\unicode[STIX]{x1D6FD}_{K}=0$
,
![]() $0.19$
,
$0.19$
,
![]() $0.58$
,
$0.58$
,
![]() $1.05$
) and one FPG, one ZPG and four APG cases for the supersonic regime (inflow Mach number
$1.05$
) and one FPG, one ZPG and four APG cases for the supersonic regime (inflow Mach number
![]() $M_{\infty ,0}=2.0$
,
$M_{\infty ,0}=2.0$
,
![]() $\unicode[STIX]{x1D6FD}_{K}=-0.18$
,
$\unicode[STIX]{x1D6FD}_{K}=-0.18$
,
![]() $0$
,
$0$
,
![]() $0.15$
,
$0.15$
,
![]() $0.42$
,
$0.42$
,
![]() $0.55$
,
$0.55$
,
![]() $0.69$
). All cases are characterized by long regions of virtually constant
$0.69$
). All cases are characterized by long regions of virtually constant
![]() $\unicode[STIX]{x1D6FD}_{K}$
.
$\unicode[STIX]{x1D6FD}_{K}$
.
The evaluation of the subsonic APG cases is consistent with the known trends gained by incompressible investigations. Whereas the
![]() $c_{f}$
-distributions, for instance, are decreased with increasing APG-strength, the shape-factor values
$c_{f}$
-distributions, for instance, are decreased with increasing APG-strength, the shape-factor values
![]() $H$
are increased. If plotted in wall units, local mean-flow profiles of subsonic APG cases are shifted down in the logarithmic layer and lifted in the wake region; the turbulent activity is significantly enhanced through the whole boundary layer, and the streamwise velocity fluctuation profiles show a second peak in the outer layer for increasing APGs.
$H$
are increased. If plotted in wall units, local mean-flow profiles of subsonic APG cases are shifted down in the logarithmic layer and lifted in the wake region; the turbulent activity is significantly enhanced through the whole boundary layer, and the streamwise velocity fluctuation profiles show a second peak in the outer layer for increasing APGs.
The interpretation of the supersonic flow field is more complex since two effects are counteracting. While streamtubes are tending to diverge in the subsonic near-wall region in the presence of APGs, they tend to converge in the supersonic part above. The resulting boundary-layer thicknesses
![]() $\unicode[STIX]{x1D6FF}_{99}$
as well as the
$\unicode[STIX]{x1D6FF}_{99}$
as well as the
![]() $c_{f}$
-distribution, for instance, are therefore in a comparable range for all PG cases. In accordance with Spina et al. (Reference Spina, Smits and Robinson1994), the switch-over value of
$c_{f}$
-distribution, for instance, are therefore in a comparable range for all PG cases. In accordance with Spina et al. (Reference Spina, Smits and Robinson1994), the switch-over value of
![]() $M_{e}\approx 1.8$
can be confirmed, below which supersonic PG TBLs are increasingly dominated by the subsonic part of the boundary layer. If plotted in wall units and compared to the ZPG case, local mean-flow profiles of supersonic cases are only slightly influenced in the logarithmic layer due to the counteracting effect of PGs and compressibility. In the wake region where both effects superpose constructively, profiles are lifted for APGs and shifted down for FPGs cases. The turbulent fluctuations are influenced in an almost identical manner as for the subsonic cases.
$M_{e}\approx 1.8$
can be confirmed, below which supersonic PG TBLs are increasingly dominated by the subsonic part of the boundary layer. If plotted in wall units and compared to the ZPG case, local mean-flow profiles of supersonic cases are only slightly influenced in the logarithmic layer due to the counteracting effect of PGs and compressibility. In the wake region where both effects superpose constructively, profiles are lifted for APGs and shifted down for FPGs cases. The turbulent fluctuations are influenced in an almost identical manner as for the subsonic cases.
For both sub- and supersonic cases the recovery factor is noticeably influenced by PGs, i.e. decreased for APG and increased for FPG cases, but stays almost constant in its spatial evolution for equilibrium cases.
A comparison of the total shear-stress distributions
![]() $\overline{\unicode[STIX]{x1D70F}}_{t}/\overline{\unicode[STIX]{x1D70F}}_{w}$
yields almost identical profiles for sub- and supersonic cases if evaluated at same
$\overline{\unicode[STIX]{x1D70F}}_{t}/\overline{\unicode[STIX]{x1D70F}}_{w}$
yields almost identical profiles for sub- and supersonic cases if evaluated at same
![]() $\unicode[STIX]{x1D6FD}_{K}$
- and
$\unicode[STIX]{x1D6FD}_{K}$
- and
![]() $Re_{\unicode[STIX]{x1D70F}}$
-values, although there is no constant stress layer near the wall anymore. An APG increases
$Re_{\unicode[STIX]{x1D70F}}$
-values, although there is no constant stress layer near the wall anymore. An APG increases
![]() $\overline{\unicode[STIX]{x1D70F}}_{t}/\overline{\unicode[STIX]{x1D70F}}_{w}$
for
$\overline{\unicode[STIX]{x1D70F}}_{t}/\overline{\unicode[STIX]{x1D70F}}_{w}$
for
![]() $y^{+}\gtrapprox 2$
due to increased turbulent activity, an FPG does the opposite. Since Mach-number and PG influences on the local mean shear-stress distributions
$y^{+}\gtrapprox 2$
due to increased turbulent activity, an FPG does the opposite. Since Mach-number and PG influences on the local mean shear-stress distributions
![]() $\overline{\unicode[STIX]{x1D707}}\unicode[STIX]{x2202}\overline{u}/\unicode[STIX]{x2202}y/\overline{\unicode[STIX]{x1D70F}}_{w}$
are virtually negligible, also the turbulent shear-stress distributions
$\overline{\unicode[STIX]{x1D707}}\unicode[STIX]{x2202}\overline{u}/\unicode[STIX]{x2202}y/\overline{\unicode[STIX]{x1D70F}}_{w}$
are virtually negligible, also the turbulent shear-stress distributions
![]() $-\overline{\unicode[STIX]{x1D70C}u^{\prime }v^{\prime }}/\overline{\unicode[STIX]{x1D70F}}_{w}$
are similar to each other for similar
$-\overline{\unicode[STIX]{x1D70C}u^{\prime }v^{\prime }}/\overline{\unicode[STIX]{x1D70F}}_{w}$
are similar to each other for similar
![]() $\unicode[STIX]{x1D6FD}_{K}$
-cases. The same holds for the turbulent stresses in the wall-normal direction
$\unicode[STIX]{x1D6FD}_{K}$
-cases. The same holds for the turbulent stresses in the wall-normal direction
![]() $\overline{\unicode[STIX]{x1D70C}v^{\prime 2}}/\overline{\unicode[STIX]{x1D70F}}_{w}$
, which thus implies the Mach-number invariance of PG effects in the compressible regime and thus the approximate validity of Morkovin’s scaling for compressible PG TBLs at least in the near equilibrium case. The Morkovin-scaled
$\overline{\unicode[STIX]{x1D70C}v^{\prime 2}}/\overline{\unicode[STIX]{x1D70F}}_{w}$
, which thus implies the Mach-number invariance of PG effects in the compressible regime and thus the approximate validity of Morkovin’s scaling for compressible PG TBLs at least in the near equilibrium case. The Morkovin-scaled
![]() $\overline{u^{\prime 2}}$
fluctuations can reproduce the respective incompressible distributions for comparable
$\overline{u^{\prime 2}}$
fluctuations can reproduce the respective incompressible distributions for comparable
![]() $\unicode[STIX]{x1D6FD}_{K}$
values with uncertainties being approximately in the same range as for ZPG cases. It is pointed out, however, that the assumption of a constant total stress region near the wall – as sometimes assumed in the scaling’s derivation – is not a necessary condition. Morkovin’s hypothesis that ‘the essential dynamics of supersonic shear flows will follow the incompressible patter’ thus still holds for TBLs subjected to PGs.
$\unicode[STIX]{x1D6FD}_{K}$
values with uncertainties being approximately in the same range as for ZPG cases. It is pointed out, however, that the assumption of a constant total stress region near the wall – as sometimes assumed in the scaling’s derivation – is not a necessary condition. Morkovin’s hypothesis that ‘the essential dynamics of supersonic shear flows will follow the incompressible patter’ thus still holds for TBLs subjected to PGs.
Implied by both the validity of Morkovin’s scaling and the two-dimensional turbulent
![]() $y$
-momentum boundary-layer equation, also the mean pressure distributions
$y$
-momentum boundary-layer equation, also the mean pressure distributions
![]() $(\overline{p}_{w\approx e}-\overline{p})/\overline{\unicode[STIX]{x1D70F}}_{w}$
and thus also the pressure fluctuations
$(\overline{p}_{w\approx e}-\overline{p})/\overline{\unicode[STIX]{x1D70F}}_{w}$
and thus also the pressure fluctuations
![]() $\sqrt{\overline{p^{\prime 2}}}/\overline{\unicode[STIX]{x1D70F}}_{w}$
are found to compare for different Mach-number cases for same
$\sqrt{\overline{p^{\prime 2}}}/\overline{\unicode[STIX]{x1D70F}}_{w}$
are found to compare for different Mach-number cases for same
![]() $\unicode[STIX]{x1D6FD}_{K}$
-values.
$\unicode[STIX]{x1D6FD}_{K}$
-values.
Concerning the van Driest transformation, the logarithmic layer of compressible PG cases can be reliably transformed into the respective nearly incompressible counterparts. The velocity in the wake region of the van Driest transformed profiles is increasingly underestimated with increasing APG strength and thus depends on the particular PG distribution. Since the wake region is also influenced by compressibility effects varying in the streamwise direction if evaluated at same
![]() $Re_{\unicode[STIX]{x1D70F}}$
, uncertainties of the van Driest transformation are not readily predictable for complex PG flows. Nevertheless, the van Driest transformation still reduces compressibility effects significantly.
$Re_{\unicode[STIX]{x1D70F}}$
, uncertainties of the van Driest transformation are not readily predictable for complex PG flows. Nevertheless, the van Driest transformation still reduces compressibility effects significantly.
Acknowledgements
The financial support by the Deutsche Forschungsgemeinschaft, DFG, under reference numbers RI680/31-1, RI680/34-1 and RI680/38-1, and the provision of computational resources on Cray XC40 by the Federal High Performance Computing Centre Stuttgart (HLRS) under grant GCS_Lamt (LAMTUR), ID=44026, are gratefully acknowledged, as well as fruitful discussions within the DFG Collaborative Research Centre SFB/TRR 40, gathered by sub-project A4.
Appendix A. Grid convergence analysis
The grid convergence analysis is performed for the most restricting subsonic
![]() $iZPG$
case and the supersonic
$iZPG$
case and the supersonic
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}$
case, see table 3(b). For the subsonic case where low Reynolds numbers are most restricting, the domain size for the analysis is reduced to
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}$
case, see table 3(b). For the subsonic case where low Reynolds numbers are most restricting, the domain size for the analysis is reduced to
![]() $(L_{x}\times L_{y}\times L_{z})/\unicode[STIX]{x1D6FF}_{99,0}=170\times 34\times 4\unicode[STIX]{x03C0}$
. This corresponds to half the length and one third the width of the domain size used in the study, see table 3(a). For the supersonic case, the analysis is performed on the domain size used in the study with
$(L_{x}\times L_{y}\times L_{z})/\unicode[STIX]{x1D6FF}_{99,0}=170\times 34\times 4\unicode[STIX]{x03C0}$
. This corresponds to half the length and one third the width of the domain size used in the study, see table 3(a). For the supersonic case, the analysis is performed on the domain size used in the study with
![]() $(L_{x}\times L_{y}\times L_{z})/\unicode[STIX]{x1D6FF}_{99,0}=500\times 34\times 12\unicode[STIX]{x03C0}$
to allow an evaluation at the most restricting high Reynolds numbers. The grid resolution is varied using 70 %, 100 % and 130 %, respectively, in the three directions for the subsonic cases, and 40 %, 60 %, 80 % and 100 % for the supersonic case, see table 4. The resulting grid resolution is summarized in table 4 in terms of wall units next to the resulting skin-friction coefficients
$(L_{x}\times L_{y}\times L_{z})/\unicode[STIX]{x1D6FF}_{99,0}=500\times 34\times 12\unicode[STIX]{x03C0}$
to allow an evaluation at the most restricting high Reynolds numbers. The grid resolution is varied using 70 %, 100 % and 130 %, respectively, in the three directions for the subsonic cases, and 40 %, 60 %, 80 % and 100 % for the supersonic case, see table 4. The resulting grid resolution is summarized in table 4 in terms of wall units next to the resulting skin-friction coefficients
![]() $c_{f}$
and the shape-factor values
$c_{f}$
and the shape-factor values
![]() $H$
. Subsonic case results are evaluated at
$H$
. Subsonic case results are evaluated at
![]() $Re_{\unicode[STIX]{x1D70F}}=480$
(averaging time
$Re_{\unicode[STIX]{x1D70F}}=480$
(averaging time
![]() $\unicode[STIX]{x0394}tu_{e}/\unicode[STIX]{x1D6FF}_{99}\approx 850$
), supersonic case results at
$\unicode[STIX]{x0394}tu_{e}/\unicode[STIX]{x1D6FF}_{99}\approx 850$
), supersonic case results at
![]() $Re_{\unicode[STIX]{x1D70F}}=700$
(averaging time about
$Re_{\unicode[STIX]{x1D70F}}=700$
(averaging time about
![]() $\unicode[STIX]{x0394}tu_{e}/\unicode[STIX]{x1D6FF}_{99}\approx 580$
).
$\unicode[STIX]{x0394}tu_{e}/\unicode[STIX]{x1D6FF}_{99}\approx 580$
).
Given in figure 28(a), cf. figure 17, the grid resolution is assessed by a comparison of the mean shear-stress distributions
![]() $\overline{\unicode[STIX]{x1D707}}(\unicode[STIX]{x2202}\overline{u}/\unicode[STIX]{x2202}y)/\overline{\unicode[STIX]{x1D70F}}_{w}$
and turbulent shear-stress distributions
$\overline{\unicode[STIX]{x1D707}}(\unicode[STIX]{x2202}\overline{u}/\unicode[STIX]{x2202}y)/\overline{\unicode[STIX]{x1D70F}}_{w}$
and turbulent shear-stress distributions
![]() $-\overline{\unicode[STIX]{x1D70C}u^{\prime \prime }v^{\prime \prime }}/\overline{\unicode[STIX]{x1D70F}}_{w}$
. According to figure 16(a) and figures 24(b) or 25(b), both the peak values
$-\overline{\unicode[STIX]{x1D70C}u^{\prime \prime }v^{\prime \prime }}/\overline{\unicode[STIX]{x1D70F}}_{w}$
. According to figure 16(a) and figures 24(b) or 25(b), both the peak values
![]() $u_{max}^{\prime +}$
and the wall-normal distributions in the outer layer of the turbulent velocity fluctuations
$u_{max}^{\prime +}$
and the wall-normal distributions in the outer layer of the turbulent velocity fluctuations
![]() $u^{\prime +}=\sqrt{\overline{u^{\prime 2}}}/u_{\unicode[STIX]{x1D70F}}$
are given in figure 28(b,c), respectively. Both values have been found to be the most sensitive ones to a poor grid resolution. As illustrated, both the results of the subsonic
$u^{\prime +}=\sqrt{\overline{u^{\prime 2}}}/u_{\unicode[STIX]{x1D70F}}$
are given in figure 28(b,c), respectively. Both values have been found to be the most sensitive ones to a poor grid resolution. As illustrated, both the results of the subsonic
![]() $iZPG\_100\,\%$
and
$iZPG\_100\,\%$
and
![]() $iZPG\_130\,\%$
cases, and of the supersonic
$iZPG\_130\,\%$
cases, and of the supersonic
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}\_80\,\%$
and
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}\_80\,\%$
and
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}\_100\,\%$
cases, are in good agreement. All given results can therefore be regarded as grid converged.
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}\_100\,\%$
cases, are in good agreement. All given results can therefore be regarded as grid converged.

Figure 28. Grid resolution analysis for the subsonic
![]() $iZPG$
case (
$iZPG$
case (
![]() $Re_{\unicode[STIX]{x1D70F}}=480$
) and supersonic
$Re_{\unicode[STIX]{x1D70F}}=480$
) and supersonic
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}}=0.69$
case (
$cAPG_{\unicode[STIX]{x1D6FD}_{K}}=0.69$
case (
![]() $Re_{\unicode[STIX]{x1D70F}}=700$
). (a) Mean shear-stress distributions
$Re_{\unicode[STIX]{x1D70F}}=700$
). (a) Mean shear-stress distributions
![]() $\overline{\unicode[STIX]{x1D707}}(\unicode[STIX]{x2202}\overline{u}/\unicode[STIX]{x2202}y)/\overline{\unicode[STIX]{x1D70F}}_{w}$
and turbulent shear-stress distributions
$\overline{\unicode[STIX]{x1D707}}(\unicode[STIX]{x2202}\overline{u}/\unicode[STIX]{x2202}y)/\overline{\unicode[STIX]{x1D70F}}_{w}$
and turbulent shear-stress distributions
![]() $-\overline{\unicode[STIX]{x1D70C}u^{\prime \prime }v^{\prime \prime }}/\overline{\unicode[STIX]{x1D70F}}_{w}$
, (b) wall-near peak value
$-\overline{\unicode[STIX]{x1D70C}u^{\prime \prime }v^{\prime \prime }}/\overline{\unicode[STIX]{x1D70F}}_{w}$
, (b) wall-near peak value
![]() $u_{max}^{\prime +}$
and (c) wall-normal distribution in the outer layer of the streamwise velocity fluctuation
$u_{max}^{\prime +}$
and (c) wall-normal distribution in the outer layer of the streamwise velocity fluctuation
![]() $u^{\prime +}=\sqrt{\overline{u^{\prime 2}}}/u_{\unicode[STIX]{x1D70F}}$
.
$u^{\prime +}=\sqrt{\overline{u^{\prime 2}}}/u_{\unicode[STIX]{x1D70F}}$
.
Table 4. Grid resolution analysis for the subsonic
![]() $iZPG$
case (
$iZPG$
case (
![]() $Re_{\unicode[STIX]{x1D70F}}=480$
) and supersonic
$Re_{\unicode[STIX]{x1D70F}}=480$
) and supersonic
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}}=0.69$
case (
$cAPG_{\unicode[STIX]{x1D6FD}_{K}}=0.69$
case (
![]() $Re_{\unicode[STIX]{x1D70F}}=700$
). Given parameters are the number of numerical grid points
$Re_{\unicode[STIX]{x1D70F}}=700$
). Given parameters are the number of numerical grid points
![]() $nx$
,
$nx$
,
![]() $ny$
and
$ny$
and
![]() $nz$
as well as the resulting grid resolutions
$nz$
as well as the resulting grid resolutions
![]() $\unicode[STIX]{x0394}x^{+}$
,
$\unicode[STIX]{x0394}x^{+}$
,
![]() $\unicode[STIX]{x0394}y_{w}^{+}$
and
$\unicode[STIX]{x0394}y_{w}^{+}$
and
![]() $\unicode[STIX]{x0394}z^{+}$
in the streamwise, wall-normal and spanwise directions, respectively. Additionally given are the skin-friction coefficient
$\unicode[STIX]{x0394}z^{+}$
in the streamwise, wall-normal and spanwise directions, respectively. Additionally given are the skin-friction coefficient
![]() $c_{f}$
and the shape factor
$c_{f}$
and the shape factor
![]() $H_{12}$
.
$H_{12}$
.

Appendix B. Vortex visualization

Figure 29. Snapshots of vortices by iso-surfaces of the
![]() $\unicode[STIX]{x1D706}_{2}$
-criterion with
$\unicode[STIX]{x1D706}_{2}$
-criterion with
![]() $\unicode[STIX]{x1D706}_{2}=-0.05u_{e}(x)/u_{\infty ,0}$
for the subsonic
$\unicode[STIX]{x1D706}_{2}=-0.05u_{e}(x)/u_{\infty ,0}$
for the subsonic
![]() $iZPG$
case and the strongest subsonic
$iZPG$
case and the strongest subsonic
![]() $iAPG_{\unicode[STIX]{x1D6FD}_{K}=1.05}$
case. Colour depicts the fluctuation amplitude of the streamwise velocity component
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=1.05}$
case. Colour depicts the fluctuation amplitude of the streamwise velocity component
![]() $u^{\prime }/u_{\infty ,0}$
. The complete main region of the simulation domain is shown, the bordered regions are depicted in detail in figure 8.
$u^{\prime }/u_{\infty ,0}$
. The complete main region of the simulation domain is shown, the bordered regions are depicted in detail in figure 8.

Figure 30. Snapshots of vortices by iso-surfaces of the
![]() $\unicode[STIX]{x1D706}_{2}$
-criterion with
$\unicode[STIX]{x1D706}_{2}$
-criterion with
![]() $\unicode[STIX]{x1D706}_{2}=-0.05u_{e}(x)/u_{\infty ,0}$
for the supersonic
$\unicode[STIX]{x1D706}_{2}=-0.05u_{e}(x)/u_{\infty ,0}$
for the supersonic
![]() $cFPG_{\unicode[STIX]{x1D6FD}_{K}=-0.18}$
case, the supersonic
$cFPG_{\unicode[STIX]{x1D6FD}_{K}=-0.18}$
case, the supersonic
![]() $cZPG$
case and the strongest supersonic
$cZPG$
case and the strongest supersonic
![]() $cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}$
case. Colour depicts the fluctuation amplitude of the streamwise velocity component
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.69}$
case. Colour depicts the fluctuation amplitude of the streamwise velocity component
![]() $u^{\prime }/u_{\infty ,0}$
. The complete main region of the simulation domain is shown, the bordered regions are depicted in detail in figure 9.
$u^{\prime }/u_{\infty ,0}$
. The complete main region of the simulation domain is shown, the bordered regions are depicted in detail in figure 9.
Figures 29 and 30 depict iso-levels of the
![]() $\unicode[STIX]{x1D706}_{2}$
-criterion computed from the non-dimensionalized flow field
$\unicode[STIX]{x1D706}_{2}$
-criterion computed from the non-dimensionalized flow field
![]() $u_{i}=u_{i}/u_{\infty ,0}$
with
$u_{i}=u_{i}/u_{\infty ,0}$
with
![]() $\unicode[STIX]{x1D706}_{2}=-0.05\,u_{e}(x)/u_{\infty ,0}$
for sub- and supersonic cases. The complete main region of the simulation domain is shown, the bordered regions are located at
$\unicode[STIX]{x1D706}_{2}=-0.05\,u_{e}(x)/u_{\infty ,0}$
for sub- and supersonic cases. The complete main region of the simulation domain is shown, the bordered regions are located at
![]() $Re_{\unicode[STIX]{x1D70F}}=490$
(FPG at
$Re_{\unicode[STIX]{x1D70F}}=490$
(FPG at
![]() $Re_{\unicode[STIX]{x1D70F}}=360$
) and are illustrated in detail in figures 8 and 9.
$Re_{\unicode[STIX]{x1D70F}}=360$
) and are illustrated in detail in figures 8 and 9.