Article contents
PSI in the case of internal wave beam reflection at a uniform slope
Published online by Cambridge University Press: 21 January 2016
Abstract
Two-dimensional numerical simulations are performed to examine internal wave reflection at a sloping boundary. Owing to reflection, the reflected wave amplitude and wavenumber increase. At low values of the incoming wave amplitude, the reflected wave beam is linear and its properties agree well with linear inviscid theory. Linear theory overestimates the reflected wave Froude number, 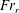 $Fr_{r}$ , for higher values of incoming wave amplitude. Nonlinearity sets in with increasing value of incoming wave Froude number,
$Fr_{r}$ , for higher values of incoming wave amplitude. Nonlinearity sets in with increasing value of incoming wave Froude number, 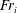 $Fr_{i}$ , leading to parametric subharmonic instability (PSI) of the reflected wave beam: two subharmonics emerge from the reflection region with frequencies
$Fr_{i}$ , leading to parametric subharmonic instability (PSI) of the reflected wave beam: two subharmonics emerge from the reflection region with frequencies 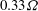 $0.33{\it\Omega}$ and
$0.33{\it\Omega}$ and 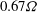 $0.67{\it\Omega}$ and wavenumbers that add up to those of the reflected wave. The amplification of Froude number due to reflection must be sufficiently large for PSI to occur implying that the off-criticality in wave angle cannot be too large. The simulations also show that, all other parameters being fixed, a threshold in beam amplitude is required for the onset of PSI in the reflected beam, consistent with results from a previous weakly-nonlinear asymptotic theory for a freely propagating finite-width beam. Growth rates of subharmonic modes at moderate reflected wave amplitude are in reasonable agreement with that theory. However, for
$0.67{\it\Omega}$ and wavenumbers that add up to those of the reflected wave. The amplification of Froude number due to reflection must be sufficiently large for PSI to occur implying that the off-criticality in wave angle cannot be too large. The simulations also show that, all other parameters being fixed, a threshold in beam amplitude is required for the onset of PSI in the reflected beam, consistent with results from a previous weakly-nonlinear asymptotic theory for a freely propagating finite-width beam. Growth rates of subharmonic modes at moderate reflected wave amplitude are in reasonable agreement with that theory. However, for  $Fr_{r}>0.5$ , small scale fluctuations becomes prominent and the subharmonic energy growth rates saturate in the simulations in contrast to the theoretical prediction. Increasing the incoming beam thickness (number of carrier wavelengths) increases the strength of PSI. Keeping the incoming Froude number constant and increasing the incoming Reynolds number by a factor of 50 does not have an effect on the unequal division of frequencies among the subharmonic modes that is found in the simulations.
$Fr_{r}>0.5$ , small scale fluctuations becomes prominent and the subharmonic energy growth rates saturate in the simulations in contrast to the theoretical prediction. Increasing the incoming beam thickness (number of carrier wavelengths) increases the strength of PSI. Keeping the incoming Froude number constant and increasing the incoming Reynolds number by a factor of 50 does not have an effect on the unequal division of frequencies among the subharmonic modes that is found in the simulations.
Information
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 11
- Cited by


