Article contents
A physical model of turbulence cascade via vortex reconnection sequence and avalanche
Published online by Cambridge University Press: 28 November 2019
Abstract
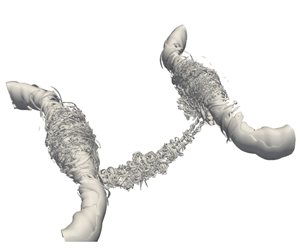
Viscous anti-parallel vortex reconnection is studied by means of direct numerical simulation for vortex Reynolds numbers  $Re$ (
$Re$ ( $\equiv \unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D708}$, circulation/viscosity) up to 40 000. To suppress the inherent symmetry breaking due to the Kelvin–Helmholtz (planar jet) instability, as prevalent in prior studies, and to better explore the progression of the mechanism details, the simulation is performed by imposing symmetry and using double-precision arithmetic. We show, for the first time, the evidence of vortex reconnection cascade scenario initially proposed by Melander and Hussain (CTR Report, 1988), who suggested that the remnant threads, following the first reconnection, undergo successive reconnections in a cascade. Secondary reconnection (the details distinctly captured and visualized at a lower
$\equiv \unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D708}$, circulation/viscosity) up to 40 000. To suppress the inherent symmetry breaking due to the Kelvin–Helmholtz (planar jet) instability, as prevalent in prior studies, and to better explore the progression of the mechanism details, the simulation is performed by imposing symmetry and using double-precision arithmetic. We show, for the first time, the evidence of vortex reconnection cascade scenario initially proposed by Melander and Hussain (CTR Report, 1988), who suggested that the remnant threads, following the first reconnection, undergo successive reconnections in a cascade. Secondary reconnection (the details distinctly captured and visualized at a lower  $Re=9000$) leads to the successive generation of numerous small-scale structures, including vortex rings, hairpin-like vortex packets and vortex tangles. As
$Re=9000$) leads to the successive generation of numerous small-scale structures, including vortex rings, hairpin-like vortex packets and vortex tangles. As  $Re$ increases, the third and higher generations of reconnection form a turbulent cloud avalanche consisting of a tangle of fine vortices. The energy is rapidly transferred to finer scales during reconnection, and a distinct- 5/3 inertial range is observed for the kinetic energy spectrum, associated with numerous resulting fine-scale bridgelets and thread filaments. In addition, we also discover an inverse cascade at large scales through the accumulation of bridgelets. The separation distance
$Re$ increases, the third and higher generations of reconnection form a turbulent cloud avalanche consisting of a tangle of fine vortices. The energy is rapidly transferred to finer scales during reconnection, and a distinct- 5/3 inertial range is observed for the kinetic energy spectrum, associated with numerous resulting fine-scale bridgelets and thread filaments. In addition, we also discover an inverse cascade at large scales through the accumulation of bridgelets. The separation distance  $\unicode[STIX]{x1D6FF}(t)$ before the first reconnection is found to scale as
$\unicode[STIX]{x1D6FF}(t)$ before the first reconnection is found to scale as  $t^{3/4}$, which is different from the typical 1/2 scaling for classical and quantum vortex filament reconnections. Both peak enstrophy and its production rate grow with
$t^{3/4}$, which is different from the typical 1/2 scaling for classical and quantum vortex filament reconnections. Both peak enstrophy and its production rate grow with  $Re$ faster than the power law suggested by Hussain and Duraisamy (Phys. Fluids, vol. 23, 2011, 021701). Our simulations not only reveal the detailed mechanisms of high-
$Re$ faster than the power law suggested by Hussain and Duraisamy (Phys. Fluids, vol. 23, 2011, 021701). Our simulations not only reveal the detailed mechanisms of high- $Re$ reconnection, but also shed light on the physics of turbulence cascade and present the reconnection avalanche as a realistic physical model for turbulence cascade.
$Re$ reconnection, but also shed light on the physics of turbulence cascade and present the reconnection avalanche as a realistic physical model for turbulence cascade.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
Yao and Hussain supplementary movie 1
Time evolution of vorticity magnitude isosurfaces at 40% of maximum initial vorticity (shaded with contours of axial vorticity) for vortex reconnection at Re = 9000.
Yao and Hussain supplementary movie 2
Time evolution of λ_2 isosurfaces of for vortex reconnection at Re = 9000.
- 57
- Cited by

