Article contents
On the propagation of gravity currents over and through a submerged array of circular cylinders
Published online by Cambridge University Press: 13 October 2017
Abstract
The propagation of full-depth lock-exchange bottom gravity currents past a submerged array of circular cylinders is investigated using laboratory experiments and large eddy simulations. Firstly, to investigate the front velocity of gravity currents across the whole range of array density 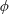 $\unicode[STIX]{x1D719}$ (i.e. the volume fraction of solids), the array is densified from a flat bed (
$\unicode[STIX]{x1D719}$ (i.e. the volume fraction of solids), the array is densified from a flat bed ( 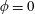 $\unicode[STIX]{x1D719}=0$ ) towards a solid slab (
$\unicode[STIX]{x1D719}=0$ ) towards a solid slab ( 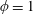 $\unicode[STIX]{x1D719}=1$ ) under a particular submergence ratio
$\unicode[STIX]{x1D719}=1$ ) under a particular submergence ratio 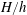 $H/h$ , where
$H/h$ , where  $H$ is the flow depth and
$H$ is the flow depth and 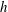 $h$ is the array height. The time-averaged front velocity in the slumping phase of the gravity current is found to first decrease and then increase with increasing
$h$ is the array height. The time-averaged front velocity in the slumping phase of the gravity current is found to first decrease and then increase with increasing 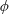 $\unicode[STIX]{x1D719}$ . Next, a new geometrical framework consisting of a streamwise array density
$\unicode[STIX]{x1D719}$ . Next, a new geometrical framework consisting of a streamwise array density 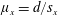 $\unicode[STIX]{x1D707}_{x}=d/s_{x}$ and a spanwise array density
$\unicode[STIX]{x1D707}_{x}=d/s_{x}$ and a spanwise array density  $\unicode[STIX]{x1D707}_{y}=d/s_{y}$ is proposed to account for organized but non-equidistant arrays (
$\unicode[STIX]{x1D707}_{y}=d/s_{y}$ is proposed to account for organized but non-equidistant arrays ( 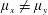 $\unicode[STIX]{x1D707}_{x}\neq \unicode[STIX]{x1D707}_{y}$ ), where
$\unicode[STIX]{x1D707}_{x}\neq \unicode[STIX]{x1D707}_{y}$ ), where 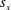 $s_{x}$ and
$s_{x}$ and 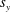 $s_{y}$ are the streamwise and spanwise cylinder spacings, respectively, and
$s_{y}$ are the streamwise and spanwise cylinder spacings, respectively, and 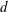 $d$ is the cylinder diameter. It is argued that this two-dimensional parameter space can provide a more quantitative and unambiguous description of the current–array interaction compared with the array density given by
$d$ is the cylinder diameter. It is argued that this two-dimensional parameter space can provide a more quantitative and unambiguous description of the current–array interaction compared with the array density given by 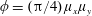 $\unicode[STIX]{x1D719}=(\unicode[STIX]{x03C0}/4)\unicode[STIX]{x1D707}_{x}\unicode[STIX]{x1D707}_{y}$ . Both in-line and staggered arrays are investigated. Four dynamically different flow regimes are identified: (i) through-flow propagating in the array interior subject to individual cylinder wakes (
$\unicode[STIX]{x1D719}=(\unicode[STIX]{x03C0}/4)\unicode[STIX]{x1D707}_{x}\unicode[STIX]{x1D707}_{y}$ . Both in-line and staggered arrays are investigated. Four dynamically different flow regimes are identified: (i) through-flow propagating in the array interior subject to individual cylinder wakes ( 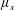 $\unicode[STIX]{x1D707}_{x}$ : small for in-line array and arbitrary for staggered array;
$\unicode[STIX]{x1D707}_{x}$ : small for in-line array and arbitrary for staggered array; 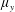 $\unicode[STIX]{x1D707}_{y}$ : small); (ii) over-flow propagating on the top of the array subject to vertical convective instability (
$\unicode[STIX]{x1D707}_{y}$ : small); (ii) over-flow propagating on the top of the array subject to vertical convective instability ( 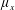 $\unicode[STIX]{x1D707}_{x}$ : large;
$\unicode[STIX]{x1D707}_{x}$ : large; 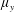 $\unicode[STIX]{x1D707}_{y}$ : large); (iii) plunging-flow climbing sparse close-to-impermeable rows of cylinders with minor streamwise intrusion (
$\unicode[STIX]{x1D707}_{y}$ : large); (iii) plunging-flow climbing sparse close-to-impermeable rows of cylinders with minor streamwise intrusion ( 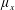 $\unicode[STIX]{x1D707}_{x}$ : small;
$\unicode[STIX]{x1D707}_{x}$ : small; 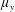 $\unicode[STIX]{x1D707}_{y}$ : large); and (iv) skimming-flow channelized by an in-line array into several subcurrents with strong wake sheltering (
$\unicode[STIX]{x1D707}_{y}$ : large); and (iv) skimming-flow channelized by an in-line array into several subcurrents with strong wake sheltering ( 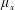 $\unicode[STIX]{x1D707}_{x}$ : large;
$\unicode[STIX]{x1D707}_{x}$ : large; 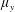 $\unicode[STIX]{x1D707}_{y}$ : small). The most remarkable difference between in-line and staggered arrays is the non-existence of skimming-flow in the latter due to the flow interruption by the offset rows. Our analysis reveals that as
$\unicode[STIX]{x1D707}_{y}$ : small). The most remarkable difference between in-line and staggered arrays is the non-existence of skimming-flow in the latter due to the flow interruption by the offset rows. Our analysis reveals that as 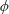 $\unicode[STIX]{x1D719}$ increases, the change of flow regime from through-flow towards over- or skimming-flow is responsible for increasing the gravity current front velocity.
$\unicode[STIX]{x1D719}$ increases, the change of flow regime from through-flow towards over- or skimming-flow is responsible for increasing the gravity current front velocity.
Information
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 28
- Cited by


