Published online by Cambridge University Press: 20 October 2009
In this paper, the available potential energy (APE) framework of Winters et al. (J. Fluid Mech., vol. 289, 1995, p. 115) is extended to the fully compressible Navier–Stokes equations, with the aims of clarifying (i) the nature of the energy conversions taking place in turbulent thermally stratified fluids; and (ii) the role of surface buoyancy fluxes in the Munk & Wunsch (Deep-Sea Res., vol. 45, 1998, p. 1977) constraint on the mechanical energy sources of stirring required to maintain diapycnal mixing in the oceans. The new framework reveals that the observed turbulent rate of increase in the background gravitational potential energy GPEr, commonly thought to occur at the expense of the diffusively dissipated APE, actually occurs at the expense of internal energy, as in the laminar case. The APE dissipated by molecular diffusion, on the other hand, is found to be converted into internal energy (IE), similar to the viscously dissipated kinetic energy KE. Turbulent stirring, therefore, does not introduce a new APE/GPEr mechanical-to-mechanical energy conversion, but simply enhances the existing IE/GPEr conversion rate, in addition to enhancing the viscous dissipation and the entropy production rates. This, in turn, implies that molecular diffusion contributes to the dissipation of the available mechanical energy ME = APE + KE, along with viscous dissipation. This result has important implications for the interpretation of the concepts of mixing efficiency γmixing and flux Richardson number Rf, for which new physically based definitions are proposed and contrasted with previous definitions.
The new framework allows for a more rigorous and general re-derivation from the first principles of Munk & Wunsch (1998, hereafter MW98)'s constraint, also valid for a non-Boussinesq ocean:
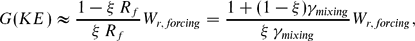 where G(KE) is the work rate done by the mechanical forcing, Wr, forcing is the rate of loss of GPEr due to high-latitude cooling and ξ is a nonlinearity parameter such that ξ = 1 for a linear equation of state (as considered by MW98), but ξ < 1 otherwise. The most important result is that G(APE), the work rate done by the surface buoyancy fluxes, must be numerically as large as Wr, forcing and, therefore, as important as the mechanical forcing in stirring and driving the oceans. As a consequence, the overall mixing efficiency of the oceans is likely to be larger than the value γmixing = 0.2 presently used, thereby possibly eliminating the apparent shortfall in mechanical stirring energy that results from using γmixing = 0.2 in the above formula.
where G(KE) is the work rate done by the mechanical forcing, Wr, forcing is the rate of loss of GPEr due to high-latitude cooling and ξ is a nonlinearity parameter such that ξ = 1 for a linear equation of state (as considered by MW98), but ξ < 1 otherwise. The most important result is that G(APE), the work rate done by the surface buoyancy fluxes, must be numerically as large as Wr, forcing and, therefore, as important as the mechanical forcing in stirring and driving the oceans. As a consequence, the overall mixing efficiency of the oceans is likely to be larger than the value γmixing = 0.2 presently used, thereby possibly eliminating the apparent shortfall in mechanical stirring energy that results from using γmixing = 0.2 in the above formula.