Article contents
On Langmuir circulation in 1 : 2 and 1 : 3 resonance
Published online by Cambridge University Press: 09 October 2019
Abstract
This paper is concerned with the nonlinear dynamics of spanwise periodic longitudinal vortex modes (Langmuir circulation (LC)) that arise through the instability of two-dimensional periodic flows (waves) in a non-stratified uniformly sheared layer of finite depth. Of particular interest is the excitation of the vortex modes either in the absence of interaction or in resonance, as described by nonlinear amplitude equations built upon the mean field Craik–Leibovich (CL) equations. Since Y-junctions in the surface footprints of Langmuir circulation indicate sporadic increases (doubling) in spacing as they evolve to the scale of sports stadiums, interest is focused on bifurcations that instigate such changes. To that end, surface patterns arising from the linear and nonlinear excitation of the vortex modes are explored, subject to two parameters: a Rayleigh number 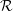 ${\mathcal{R}}$ present in the CL equations and a symmetry breaking parameter
${\mathcal{R}}$ present in the CL equations and a symmetry breaking parameter 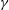 $\unicode[STIX]{x1D6FE}$ in the mixed free surface boundary conditions that relax to those at the layer bottom where
$\unicode[STIX]{x1D6FE}$ in the mixed free surface boundary conditions that relax to those at the layer bottom where 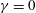 $\unicode[STIX]{x1D6FE}=0$. Looking first to linear instability, it is found as
$\unicode[STIX]{x1D6FE}=0$. Looking first to linear instability, it is found as 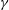 $\unicode[STIX]{x1D6FE}$ increases from zero to unity, that the neutral curves evolve from asymmetric near onset to almost symmetric. The nonlinear dynamics of single modes is then studied via an amplitude equation of Ginzburg–Landau type. While typically of cubic order when the bifurcation is supercritical (as it is here) and the neutral curves are parabolic, the Ginzburg–Landau equation must instead here be of quartic order to recover the asymmetry in the neutral curves. This equation is then subjected to an Eckhaus instability analysis, which indicates that linearly unstable subharmonics mostly reside outside the Eckhaus boundary, thereby excluding them as candidates for excitation. The surface pattern is then largely unchanged from its linear counterpart, although the character of the pattern does change when
$\unicode[STIX]{x1D6FE}$ increases from zero to unity, that the neutral curves evolve from asymmetric near onset to almost symmetric. The nonlinear dynamics of single modes is then studied via an amplitude equation of Ginzburg–Landau type. While typically of cubic order when the bifurcation is supercritical (as it is here) and the neutral curves are parabolic, the Ginzburg–Landau equation must instead here be of quartic order to recover the asymmetry in the neutral curves. This equation is then subjected to an Eckhaus instability analysis, which indicates that linearly unstable subharmonics mostly reside outside the Eckhaus boundary, thereby excluding them as candidates for excitation. The surface pattern is then largely unchanged from its linear counterpart, although the character of the pattern does change when 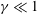 $\unicode[STIX]{x1D6FE}\ll 1$ as a result of symmetry breaking. Attention is then turned to strong resonance between the least stable linear mode and a sub-harmonic of it, as described by coupled nonlinear amplitude equations of Stuart-Landau type. Both 1 : 2 and 1 : 3 resonant interactions are considered. Phase plots and bifurcation diagrams are employed to reveal classes of solution that can occur. Dominant over much of the
$\unicode[STIX]{x1D6FE}\ll 1$ as a result of symmetry breaking. Attention is then turned to strong resonance between the least stable linear mode and a sub-harmonic of it, as described by coupled nonlinear amplitude equations of Stuart-Landau type. Both 1 : 2 and 1 : 3 resonant interactions are considered. Phase plots and bifurcation diagrams are employed to reveal classes of solution that can occur. Dominant over much of the  ${\mathcal{R}}$-
${\mathcal{R}}$-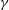 $\unicode[STIX]{x1D6FE}$ range considered are non-travelling pure- and mixed-mode equilibrium solutions that act singly or together. To wit, pure modes solutions alone act to realise windrows with spacings in accord with linear theory, while bistability can realise Y-junctions and, depending upon initial conditions, double or even triple the dominant spacing of LC.
$\unicode[STIX]{x1D6FE}$ range considered are non-travelling pure- and mixed-mode equilibrium solutions that act singly or together. To wit, pure modes solutions alone act to realise windrows with spacings in accord with linear theory, while bistability can realise Y-junctions and, depending upon initial conditions, double or even triple the dominant spacing of LC.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 1
- Cited by

