Article contents
On incident shock wave/boundary layer interactions under the influence of expansion corner
Published online by Cambridge University Press: 03 June 2024
Abstract
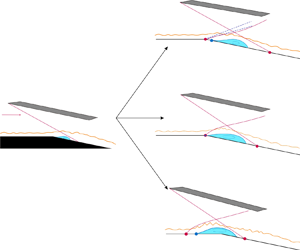
Cowl-induced incident shock wave/boundary layer interactions (ISWBLIs) under the influence of shoulder expansion represent one of the dominant phenomena in supersonic inlets. To provide a more comprehensive understanding of how an expansion corner affects the ISWBLI, a detailed experimental and analytical study is performed in a Mach 2.73 flow in this work. Pressure measurement, schlieren photography and surface oil-flow visualisation are used to record flow features, including the pressure distribution, separation extent and surface-flow topological structures. Our results reveal three types of ISWBLIs influenced by the expansion corner. When the shock intensity is weak, the separation is small scale with the expansion waves emanating from the expansion corner. This is the first type of expansion-corner-affected ISWBLI (EC-ISWBLI). When the incident shock wave is strong, large-scale separation occurs, accompanied by the disappearance of expansion waves, forming the second type of EC-SWBLI. The expansion corner induces a ‘lock-in’ effect in which the separation onset is consistently locked near the expansion corner regardless of the incident shock intensity and impingement position. The third type of EC-ISWBLI occurs when the shock is sufficiently strong and the impingement point is close to the expansion corner. In this interaction, the ‘lock-in’ effect ceases to manifest. Moreover, a shock polar-incorporating inviscid model is employed to elucidate the shock patterns. Two criteria are established by combining free interaction theory with this model. The first criterion provides valuable insights into the evolution of separations with a minimal overall pressure rise and the second criterion determines the threshold for the occurrence of the ‘lock-in’ effect.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press
References
- 5
- Cited by


