Published online by Cambridge University Press: 23 December 2019
Cavitating flow over a circular cylinder is investigated over a range of cavitation numbers ( $\unicode[STIX]{x1D70E}=5$ to
$\unicode[STIX]{x1D70E}=5$ to  $0.5$) for both laminar (at Reynolds number
$0.5$) for both laminar (at Reynolds number  $(Re)=200$) and turbulent (at
$(Re)=200$) and turbulent (at  $Re=3900$) regimes. We observe non-cavitating, cyclic and transitional cavitation regimes with reduction in free-stream
$Re=3900$) regimes. We observe non-cavitating, cyclic and transitional cavitation regimes with reduction in free-stream  $\unicode[STIX]{x1D70E}$. The cavitation inside the Kármán vortices in the cyclic regime, is significantly altered by the onset of ‘condensation front’ propagation in the transitional regime. At the transition, an order of magnitude jump in shedding Strouhal number (
$\unicode[STIX]{x1D70E}$. The cavitation inside the Kármán vortices in the cyclic regime, is significantly altered by the onset of ‘condensation front’ propagation in the transitional regime. At the transition, an order of magnitude jump in shedding Strouhal number ( $St$) is observed as the dominant frequency shifts from periodic vortex shedding in the cyclic regime, to irregular–regular vortex shedding in the transitional regime. In addition, a peak in pressure fluctuations, and a maximum in
$St$) is observed as the dominant frequency shifts from periodic vortex shedding in the cyclic regime, to irregular–regular vortex shedding in the transitional regime. In addition, a peak in pressure fluctuations, and a maximum in  $St$ versus
$St$ versus  $\unicode[STIX]{x1D70E}$ based on cavity length are observed at the transition. Shedding characteristics in each regime are discussed using dynamic mode decomposition. A numerical method based on the homogeneous mixture model, fully compressible formulation and finite rate mass transfer developed by Gnanaskandan & Mahesh (Intl J. Multiphase Flow, vol. 70, 2015, pp. 22–34) is extended to include the effects of non-condensable gas (NCG). It is demonstrated that the condensation fronts observed in the transitional regime are supersonic (referred to as ‘condensation shocks’). In the presence of NCG, multiple condensation shocks in a given cycle are required for complete cavity condensation and detachment, as compared to a single condensation shock when only vapour is present. This is explained by the reduction in pressure ratio across the shock in the presence of NCG, effectively reducing its strength. In addition, at
$\unicode[STIX]{x1D70E}$ based on cavity length are observed at the transition. Shedding characteristics in each regime are discussed using dynamic mode decomposition. A numerical method based on the homogeneous mixture model, fully compressible formulation and finite rate mass transfer developed by Gnanaskandan & Mahesh (Intl J. Multiphase Flow, vol. 70, 2015, pp. 22–34) is extended to include the effects of non-condensable gas (NCG). It is demonstrated that the condensation fronts observed in the transitional regime are supersonic (referred to as ‘condensation shocks’). In the presence of NCG, multiple condensation shocks in a given cycle are required for complete cavity condensation and detachment, as compared to a single condensation shock when only vapour is present. This is explained by the reduction in pressure ratio across the shock in the presence of NCG, effectively reducing its strength. In addition, at  $\unicode[STIX]{x1D70E}=0.85$ (near transition from the cyclic to the transitional regime), the presence of NCG suppresses the low frequency irregular–regular vortex shedding. Vorticity transport at
$\unicode[STIX]{x1D70E}=0.85$ (near transition from the cyclic to the transitional regime), the presence of NCG suppresses the low frequency irregular–regular vortex shedding. Vorticity transport at  $Re=3900$, in the transitional regime, indicates that the region of attached cavity is nearly two-dimensional, with very low vorticity, affecting Kármán shedding in the near wake. Majority of vortex stretching/tilting and vorticity production is observed following the cavity trailing edge. In addition, the boundary-layer separation point is found to be strongly dependent on the amounts of vapour and gas in the free stream for both laminar and turbulent regimes.
$Re=3900$, in the transitional regime, indicates that the region of attached cavity is nearly two-dimensional, with very low vorticity, affecting Kármán shedding in the near wake. Majority of vortex stretching/tilting and vorticity production is observed following the cavity trailing edge. In addition, the boundary-layer separation point is found to be strongly dependent on the amounts of vapour and gas in the free stream for both laminar and turbulent regimes.
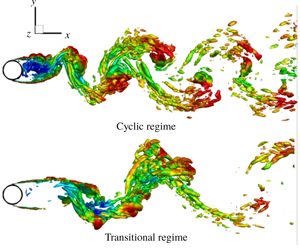
Fig 5(a). Instantaneous total void fraction contour for the cyclic regime for Case B.
Fig 5(b,c). Instantaneous total void fraction contour for the transitional regime for Case B.
Figure_1: Vapor volume fraction fluctuation for Case A200 at sigma=1.
Figure_2: NCG volume fraction fluctuation for Case A200 at sigma=1.
Figure_3: Average local cavitation number for Case A200 at sigma=1.
Figure_4: Average velocity magnitude for Case A200 at sigma=1.
Figure_5: Vapor volume fraction fluctuation for Case A200 at sigma=0.7.
Figure_6: NCG volume fraction fluctuation for Case A200 at sigma=0.7.