Article contents
Non-Boussinesq gravity currents and surface waves generated by lock release in a circular-section channel: theoretical and experimental investigation
Published online by Cambridge University Press: 02 May 2019
Abstract
We present a combined theoretical and experimental study of lock-release inertial gravity currents (GCs) propagating in a horizontal channel of circular cross-section with open-top surface in the non-Boussinesq regime. A two-layer shallow-water (SW) model is developed for a generic shape of the cross-section with open top, and then implemented in a finite difference numerical code for the solution in a circular-cross-section channel of the type used in the experiments. The model predicts propagation with (almost) constant speed for a fairly long distance, accompanied by a depression of the ambient free open-top surface behind the front of the current. Sixteen experiments were conducted with a density ratio 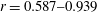 $r=0.587{-}0.939$ in full-depth and part-depth release conditions, measuring the front speed and the free-surface time series at four cross-sections. The channel was a circular tube 409 cm long, with a radius of 9.5 cm; the lengths of the locks were 52 and 103.5 cm. Density contrast was obtained by adding sodium chloride and dipotassium phosphate to fresh water. The theoretical values of the front speed and of the depression overestimate the experimental values, but they predict correctly their trend for varying parameters and provide reliable insights into the underlying mechanisms. In particular, we demonstrate that the circular cross-section increases the speed of propagation as compared to the standard rectangular cross-section case (for the same initial height and density ratio). The discrepancies between the SW predictions and the present experiments are of the same order of magnitude as those of previously published results for simpler systems (Boussinesq, rectangular). In addition to the depression, which is a wave bound to, and following the front of, the GC, the system also displays two kinds of free-surface waves, namely the initial bump (its amplitude is of the same order as the depression) and some short-length and low-amplitude waves in the tail of the bump. These free waves propagate with a celerity well predicted by the ‘fast’ eigenvalues of the mathematical model. Comparison is provided with the celerity of a solitary wave. It is expected that discrepancies between theory and experiments can be partly attributed to the presence of these waves. The reported insights and SW prediction method can be applied to a variety of cross-sections of practical interest (triangles, trapezoids, etc.).
$r=0.587{-}0.939$ in full-depth and part-depth release conditions, measuring the front speed and the free-surface time series at four cross-sections. The channel was a circular tube 409 cm long, with a radius of 9.5 cm; the lengths of the locks were 52 and 103.5 cm. Density contrast was obtained by adding sodium chloride and dipotassium phosphate to fresh water. The theoretical values of the front speed and of the depression overestimate the experimental values, but they predict correctly their trend for varying parameters and provide reliable insights into the underlying mechanisms. In particular, we demonstrate that the circular cross-section increases the speed of propagation as compared to the standard rectangular cross-section case (for the same initial height and density ratio). The discrepancies between the SW predictions and the present experiments are of the same order of magnitude as those of previously published results for simpler systems (Boussinesq, rectangular). In addition to the depression, which is a wave bound to, and following the front of, the GC, the system also displays two kinds of free-surface waves, namely the initial bump (its amplitude is of the same order as the depression) and some short-length and low-amplitude waves in the tail of the bump. These free waves propagate with a celerity well predicted by the ‘fast’ eigenvalues of the mathematical model. Comparison is provided with the celerity of a solitary wave. It is expected that discrepancies between theory and experiments can be partly attributed to the presence of these waves. The reported insights and SW prediction method can be applied to a variety of cross-sections of practical interest (triangles, trapezoids, etc.).
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 7
- Cited by

