Article contents
The influence of heating on liquid jet spreading and hydraulic jump
Published online by Cambridge University Press: 29 November 2019
Abstract
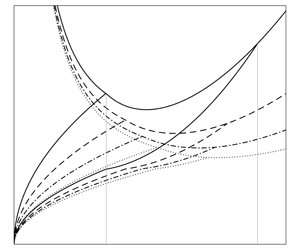
The free-surface flow and thermal fields formed by an axisymmetric liquid jet impinging on a circular heated disk are examined theoretically. The disk is maintained either at a prescribed heat flux or temperature. The study explores the effect of inertia, wall heat flux and wall temperature on the momentum and thermal boundary layers as well as the film thickness and the location and height of the hydraulic jump. Only non-metallic liquids are considered, for which the kinematic viscosity is generally larger than the thermal diffusivity, causing the thermal boundary layer to remain thinner than the momentum boundary layer. The effect of surface tension resulting in the Marangoni stress at the free surface and the hoop stress at the jump is also explored. Our results corroborate well existing experimental, theoretical and numerical studies. Both the momentum and thermal boundary layers are found to decrease with increased inertia or thermal input at the disk. The thermal boundary layer is found to always reach the free surface for an imposed constant wall heat flux. The two transition locations where the boundary layers reach the free surface move downstream with inertia but move in opposite directions with increasing wall heat flux or wall temperature. Enhanced heating from the wall also tends to increase the jump radius and depress its height. More importantly, the hydraulic jump leads to a shock-type drop in the Nusselt number, confirming existing numerical findings. Finally, we show that the Nusselt number is independent of the wall temperature for a fluid of constant properties.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 18
- Cited by

