1. Introduction
Turbulent convective energy coalesces into large coherent flow structures. This is one of the key features that delineates many geo- and astrophysical systems, and also manifests in numerous industrial applications. Often, these systems are subjected to additional, stabilizing forces, such as centrifugal and Coriolis forces due to rotation, or Lorentz forces due to magnetic fields. These forces can substantially affect the flow structures and therefore, the heat and momentum transport of convective systems.
The simplest physical model to study thermally driven flows is the so-called Rayleigh–Bénard convection (RBC), where the driving force is a temperature gradient ![]() $\boldsymbol {\nabla } T$ between a warmer bottom and a cooler top (Ahlers, Grossmann & Lohse Reference Ahlers, Grossmann and Lohse2009; Chillà & Schumacher Reference Chillà and Schumacher2012). An important outcome of RBC studies is the scaling relations for the global heat and momentum transport, expressed non-dimensionally in terms of the Nusselt number (
$\boldsymbol {\nabla } T$ between a warmer bottom and a cooler top (Ahlers, Grossmann & Lohse Reference Ahlers, Grossmann and Lohse2009; Chillà & Schumacher Reference Chillà and Schumacher2012). An important outcome of RBC studies is the scaling relations for the global heat and momentum transport, expressed non-dimensionally in terms of the Nusselt number (![]() $Nu$) and Reynolds number (
$Nu$) and Reynolds number (![]() $Re$), respectively (Grossmann & Lohse Reference Grossmann and Lohse2002; Stevens et al. Reference Stevens, Poel, Grossmann and Lohse2013).
$Re$), respectively (Grossmann & Lohse Reference Grossmann and Lohse2002; Stevens et al. Reference Stevens, Poel, Grossmann and Lohse2013).
When stabilizing forces such as rotation (Guervilly, Hughes & Jones Reference Guervilly, Hughes and Jones2014; Stellmach et al. Reference Stellmach, Lischper, Julien, Vasil, Cheng, Ribeiro, King and Aurnou2014), geometrical confinements (Daya & Ecke Reference Daya and Ecke2001; Huang et al. Reference Huang, Kaczorowski, Ni and Xia2013) or static magnetic fields are added to highly nonlinear systems such as RBC, unexpected features are encountered (Chong et al. Reference Chong, Yang, Huang, Zhong, Stevens, Verzicco, Lohse and Xia2017; Aurnou et al. Reference Aurnou, Bertin, Grannan, Horn and Vogt2018). For instance, studies have shown that rotation around a vertical axis has a strong influence on the flow structure and consequently the heat transport. Although it is well known that the Coriolis force has a stabilizing effect (Proudman Reference Proudman1916; Taylor Reference Taylor1917; Chandrasekhar Reference Chandrasekhar1961), it was found that the application of moderate forces can even enhance scalar transport (Rossby Reference Rossby1969; Zhong, Ecke & Steinberg Reference Zhong, Ecke and Steinberg1993; Liu & Ecke Reference Liu and Ecke2009; Stevens et al. Reference Stevens, Zhong, Clercx, Ahlers and Lohse2009; Wei, Weiss & Ahlers Reference Wei, Weiss and Ahlers2015; Weiss, Wei & Ahlers Reference Weiss, Wei and Ahlers2016; Chong et al. Reference Chong, Yang, Huang, Zhong, Stevens, Verzicco, Lohse and Xia2017).
Similarly, magnetic fields exert an influence on electrically conducting fluids by the induction of eddy currents ![]() $\boldsymbol {j} = \sigma (\boldsymbol {E} + \boldsymbol {u} \times \boldsymbol {B}$) which give rise to a corresponding Lorentz force
$\boldsymbol {j} = \sigma (\boldsymbol {E} + \boldsymbol {u} \times \boldsymbol {B}$) which give rise to a corresponding Lorentz force ![]() $\boldsymbol {f}_l = \boldsymbol {j} \times \boldsymbol {B}$ that acts on the fluid. Here,
$\boldsymbol {f}_l = \boldsymbol {j} \times \boldsymbol {B}$ that acts on the fluid. Here, ![]() $\sigma$ is the electrical conductivity,
$\sigma$ is the electrical conductivity, ![]() $\boldsymbol {E}$ is the electric field,
$\boldsymbol {E}$ is the electric field, ![]() $\boldsymbol {u}$ is the velocity and
$\boldsymbol {u}$ is the velocity and ![]() $\boldsymbol {B}$ is the magnetic field. A static magnetic field cannot generate any flow from a quiescent state, however, it can reorganize an electrically conducting flow field so as to minimize the Joule dissipation (Davidson Reference Davidson1995). This is a direct consequence of a reduction of the velocity gradients along the magnetic field direction due to the induced eddy currents (Sommeria & Moreau Reference Sommeria and Moreau1982; Pothérat & Klein Reference Pothérat and Klein2017).
$\boldsymbol {B}$ is the magnetic field. A static magnetic field cannot generate any flow from a quiescent state, however, it can reorganize an electrically conducting flow field so as to minimize the Joule dissipation (Davidson Reference Davidson1995). This is a direct consequence of a reduction of the velocity gradients along the magnetic field direction due to the induced eddy currents (Sommeria & Moreau Reference Sommeria and Moreau1982; Pothérat & Klein Reference Pothérat and Klein2017).
In thermal convection in liquid metal, the orientation of the applied magnetic field with respect to the temperature gradient ![]() $\boldsymbol {\nabla } T$, plays a pivotal role on the details of the resulting flow field. Two field orientations are possible: vertical and horizontal. A vertical magnetic field (
$\boldsymbol {\nabla } T$, plays a pivotal role on the details of the resulting flow field. Two field orientations are possible: vertical and horizontal. A vertical magnetic field (![]() $\boldsymbol {B} \parallel \boldsymbol {\nabla } T$) inhibits the onset of liquid metal convection and the heat transport decreases monotonically with increasing magnetic field strength, due to a strong suppression of the bulk flow (Cioni, Chaumat & Sommeria Reference Cioni, Chaumat and Sommeria2000; Aurnou & Olson Reference Aurnou and Olson2001; Burr & Müller Reference Burr and Müller2001; Liu, Krasnov & Schumacher Reference Liu, Krasnov and Schumacher2018; Yan et al. Reference Yan, Calkins, Maffei, Julien, Tobias and Marti2019; Zürner et al. Reference Zürner, Schindler, Vogt, Eckert and Schumacher2020). Recently, it was shown that convection in fluid with a Prandtl number
$\boldsymbol {B} \parallel \boldsymbol {\nabla } T$) inhibits the onset of liquid metal convection and the heat transport decreases monotonically with increasing magnetic field strength, due to a strong suppression of the bulk flow (Cioni, Chaumat & Sommeria Reference Cioni, Chaumat and Sommeria2000; Aurnou & Olson Reference Aurnou and Olson2001; Burr & Müller Reference Burr and Müller2001; Liu, Krasnov & Schumacher Reference Liu, Krasnov and Schumacher2018; Yan et al. Reference Yan, Calkins, Maffei, Julien, Tobias and Marti2019; Zürner et al. Reference Zürner, Schindler, Vogt, Eckert and Schumacher2020). Recently, it was shown that convection in fluid with a Prandtl number ![]() $Pr = \nu/\kappa = 8$, whereby
$Pr = \nu/\kappa = 8$, whereby ![]() $\nu$ is the kinematic viscosity and
$\nu$ is the kinematic viscosity and ![]() $\kappa$ is the thermal diffusivity, and under the influence of a vertical magnetic field results in increased heat flux with increasing magnetic field strength but accompanied by a decrease in momentum transport (Lim et al. Reference Lim, Chong, Ding and Xia2019).
$\kappa$ is the thermal diffusivity, and under the influence of a vertical magnetic field results in increased heat flux with increasing magnetic field strength but accompanied by a decrease in momentum transport (Lim et al. Reference Lim, Chong, Ding and Xia2019).
A horizontal magnetic field (![]() $\boldsymbol {B} \perp \boldsymbol {\nabla } T$), however, converts the convective motion into a flow pattern of quasi-two-dimensional rolls arranged parallel to the magnetic field (Fauve, Laroche & Libchaber Reference Fauve, Laroche and Libchaber1981; Busse & Clever Reference Busse and Clever1983; Burr & Müller Reference Burr and Müller2002; Yanagisawa et al. Reference Yanagisawa, Hamano, Miyagoshi, Yamagishi, Tasaka and Takeda2013; Tasaka et al. Reference Tasaka, Igaki, Yanagisawa, Vogt, Zürner and Eckert2016; Vogt et al. Reference Vogt, Ishimi, Yanagisawa, Tasaka, Sakuraba and Eckert2018a).
$\boldsymbol {B} \perp \boldsymbol {\nabla } T$), however, converts the convective motion into a flow pattern of quasi-two-dimensional rolls arranged parallel to the magnetic field (Fauve, Laroche & Libchaber Reference Fauve, Laroche and Libchaber1981; Busse & Clever Reference Busse and Clever1983; Burr & Müller Reference Burr and Müller2002; Yanagisawa et al. Reference Yanagisawa, Hamano, Miyagoshi, Yamagishi, Tasaka and Takeda2013; Tasaka et al. Reference Tasaka, Igaki, Yanagisawa, Vogt, Zürner and Eckert2016; Vogt et al. Reference Vogt, Ishimi, Yanagisawa, Tasaka, Sakuraba and Eckert2018a).
In this paper, we report on the interaction between liquid metal convection and a static, horizontally imposed magnetic field, which is governed by two non-dimensional parameters. The Rayleigh number
is a measure of the thermal forcing that drives the convection. The strength of the stabilizing Lorentz force due to the applied magnetic field is expressed by the Chandrasekhar number
Here, ![]() $H$ is the distance between the heated and the cooled plates,
$H$ is the distance between the heated and the cooled plates, ![]() $L$ is the width of the cell,
$L$ is the width of the cell, ![]() $\Delta T$ is the imposed temperature difference between these plates,
$\Delta T$ is the imposed temperature difference between these plates, ![]() $B$ is the strength of the magnetic field,
$B$ is the strength of the magnetic field, ![]() $\rho$ is the density of the liquid metal,
$\rho$ is the density of the liquid metal, ![]() $\alpha$ is the thermal expansion coefficient,
$\alpha$ is the thermal expansion coefficient, ![]() $g$ denotes the gravitational acceleration,
$g$ denotes the gravitational acceleration, ![]() $\sigma$ is the electrical conductivity and
$\sigma$ is the electrical conductivity and ![]() $Ha$ is the Hartmann number.
$Ha$ is the Hartmann number.
The present work is a continuation of the work of Vogt et al. (Reference Vogt, Ishimi, Yanagisawa, Tasaka, Sakuraba and Eckert2018a), where the transition from a three-dimensional to a quasi-two-dimensional flow structure in liquid metal convection under the influence of a horizontal magnetic field was investigated. Vogt et al. (Reference Vogt, Ishimi, Yanagisawa, Tasaka, Sakuraba and Eckert2018a) focused on the qualitative description of large- and small-scale flow structures at different parametric combinations of Rayleigh number and Chandrasekhar number, while the main goal of this work is to investigate how this transition between flow regimes affects heat and momentum transport. Accordingly, the measuring arrangement at the experiment was extended and the number of measurements was increased significantly to allow a fine increment of the Chandrasekhar number. We find that the reorganization of the convective flow due to the magnetic field results in a significant enhancement of both heat and momentum transport. In the optimum, the convective velocities can even reach the free-fall limit ![]() $u_{ff}=\sqrt {\alpha g \Delta T H}$. In classical RBC in fluids with moderate Prandtl numbers, such as water or air, the flow velocities are well below the free-fall limit and do not exceed
$u_{ff}=\sqrt {\alpha g \Delta T H}$. In classical RBC in fluids with moderate Prandtl numbers, such as water or air, the flow velocities are well below the free-fall limit and do not exceed ![]() $u_{max}/u_{ff} \leqslant 0.2$ (Niemela & Sreenivasan Reference Niemela and Sreenivasan2003). Therefore, our measurements demonstrate how intense low
$u_{max}/u_{ff} \leqslant 0.2$ (Niemela & Sreenivasan Reference Niemela and Sreenivasan2003). Therefore, our measurements demonstrate how intense low ![]() $Pr$ magnetohydrodynamic convective flows can actually become.
$Pr$ magnetohydrodynamic convective flows can actually become.
2. Laboratory magneto-convection experiments
2.1. Experimental set-up
The experiments were conducted at the Helmholtz-Zentrum Dresden Rossendorf (HZDR). The eutectic liquid metal alloy composed of gallium, indium and tin (GaInSn, melting point of ![]() $T=10.5\,^\circ \text {C}$,
$T=10.5\,^\circ \text {C}$, ![]() $Pr=\nu / \kappa = 0.03$) was used as the working fluid (Plevachuck et al. Reference Plevachuck, Sklyarchuk, Eckert, Gerbeth and Novakovic2014). The liquid metal is contained in an aspect ratio
$Pr=\nu / \kappa = 0.03$) was used as the working fluid (Plevachuck et al. Reference Plevachuck, Sklyarchuk, Eckert, Gerbeth and Novakovic2014). The liquid metal is contained in an aspect ratio ![]() $\varGamma = L/H = 5$ rectangular vessel with a cross-section
$\varGamma = L/H = 5$ rectangular vessel with a cross-section ![]() $L^2=200 \times 200\ \mathrm {mm}^{2}$ and a height
$L^2=200 \times 200\ \mathrm {mm}^{2}$ and a height ![]() $H=40$ mm (figure 1). The sidewalls are made of 30 mm thick Polyvinyl chloride and the top and bottom are made of copper. The convection cell is wrapped in 30 mm closed-cell foam to minimize heat loss. The temperature of the top and bottom were adjusted by a constant temperature water bath which flows through channels in the copper plates. The maximum heat flux is 1500 W. The applied temperature drop between the plates is in the range
$H=40$ mm (figure 1). The sidewalls are made of 30 mm thick Polyvinyl chloride and the top and bottom are made of copper. The convection cell is wrapped in 30 mm closed-cell foam to minimize heat loss. The temperature of the top and bottom were adjusted by a constant temperature water bath which flows through channels in the copper plates. The maximum heat flux is 1500 W. The applied temperature drop between the plates is in the range ![]() $1.1\ \textrm {K} \leqslant \Delta T \leqslant 11.7\ \textrm {K}$ whereby the mean fluid temperature was kept constant at
$1.1\ \textrm {K} \leqslant \Delta T \leqslant 11.7\ \textrm {K}$ whereby the mean fluid temperature was kept constant at ![]() $T_m = 20\,^\circ \text {C}$. The Rayleigh number is in the range
$T_m = 20\,^\circ \text {C}$. The Rayleigh number is in the range ![]() $2.3 \times 10^4 \leqslant Ra \leqslant 2.6 \times 10^5$. A static, uniform horizontal magnetic field penetrates the liquid metal with a strength
$2.3 \times 10^4 \leqslant Ra \leqslant 2.6 \times 10^5$. A static, uniform horizontal magnetic field penetrates the liquid metal with a strength ![]() $0 \leqslant B \leqslant 317\ \textrm {mT}$, which gives a Chandrasekhar number range
$0 \leqslant B \leqslant 317\ \textrm {mT}$, which gives a Chandrasekhar number range ![]() $0 \leqslant Q \leqslant 6.1 \times 10^6$.
$0 \leqslant Q \leqslant 6.1 \times 10^6$.
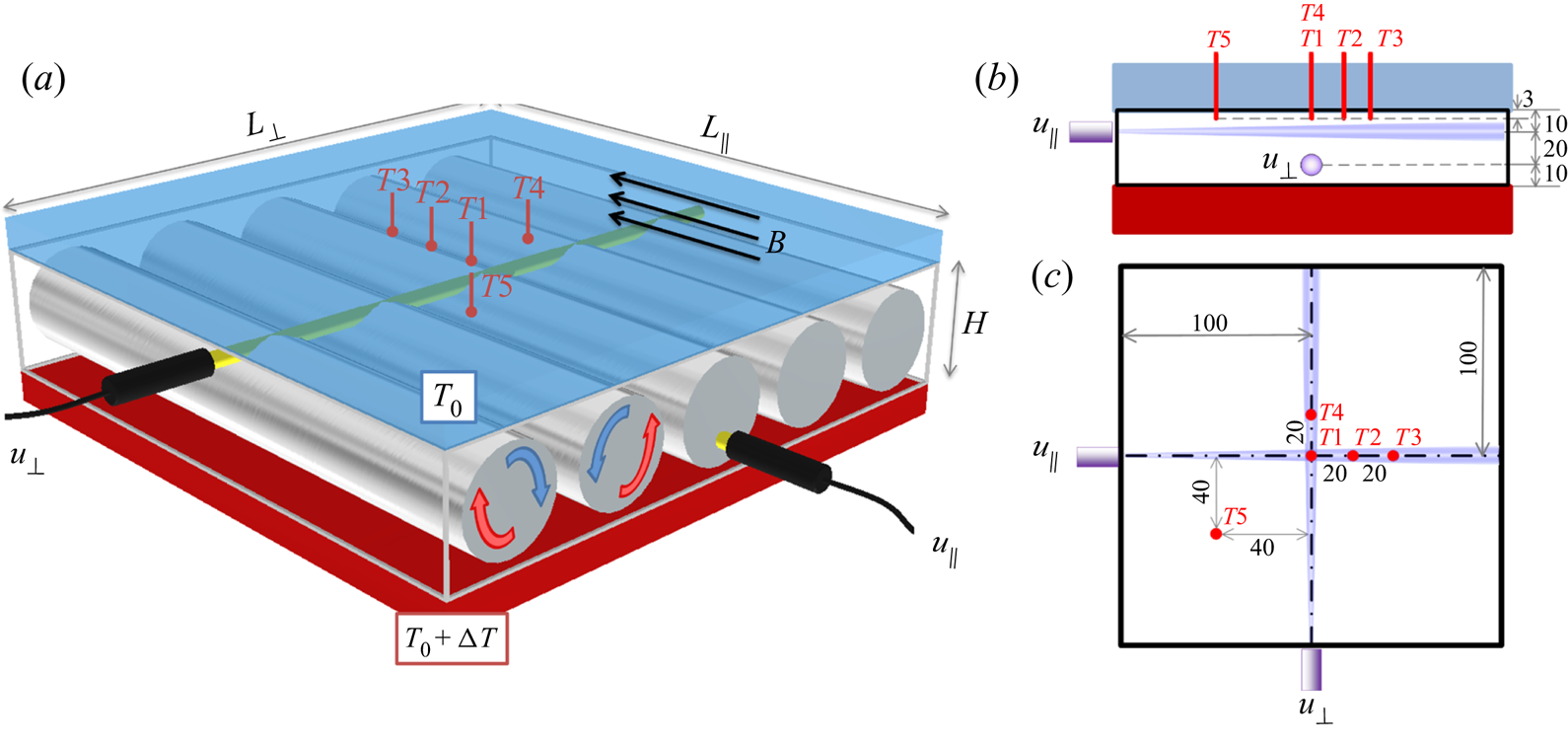
Figure 1. Schematic of the experimental set-up (a). The convection rolls (shown in grey), driven by the temperature difference ![]() $\Delta T$ between the heated bottom plate (red) and the cooled top (blue), are aligned parallel to the magnetic field
$\Delta T$ between the heated bottom plate (red) and the cooled top (blue), are aligned parallel to the magnetic field ![]() $(B)$. The velocities
$(B)$. The velocities ![]() $(u_{\parallel }, u_{\bot })$ were measured with ultrasound transducers (black tubes) parallel and perpendicular to the direction of the magnetic field. Five thermocouples
$(u_{\parallel }, u_{\bot })$ were measured with ultrasound transducers (black tubes) parallel and perpendicular to the direction of the magnetic field. Five thermocouples ![]() $(T1\text {--}T5)$ measured the temperature inside the fluid, at a distance of 3 mm from the inner edge of top plate. The side view (b) and the top view (c) schematics illustrate the positions for the ultrasound transducers and thermocouples. The units are in mm.
$(T1\text {--}T5)$ measured the temperature inside the fluid, at a distance of 3 mm from the inner edge of top plate. The side view (b) and the top view (c) schematics illustrate the positions for the ultrasound transducers and thermocouples. The units are in mm.
The fluid velocities are measured using ultrasound Doppler velocimetry (UDV), which provides instantaneous velocity profiles along two horizontal directions, as shown in figure 1. This technique is useful for non-invasively measuring velocities in opaque fluids (Brito et al. Reference Brito, Nataf, Cardin, Aubert and Masson2001; Tsuji et al. Reference Tsuji, Mizuno, Mashiko and Sano2005; Vogt, Räbiger & Eckert Reference Vogt, Räbiger and Eckert2014; Vogt, Horn & Aurnou Reference Vogt, Horn and Aurnou2020). The transducers (TR0805SS, Signal Processing SA) detect the velocity component parallel to the ultrasonic beam with resolutions of approximately 1 mm in the beam direction and 1 Hz in time. One UDV transducer measures the flow velocities perpendicular to the magnetic field (![]() $u_{\bot }$) and is located in the middle of the cell width at
$u_{\bot }$) and is located in the middle of the cell width at ![]() $L_{\parallel }/2$ and 10 mm below the upper boundary (
$L_{\parallel }/2$ and 10 mm below the upper boundary (![]() $3H/4$). A second UDV transducer measures the magnetic field parallel velocity component (
$3H/4$). A second UDV transducer measures the magnetic field parallel velocity component (![]() $u_{\parallel }$) and is also located in the middle of the cell width at
$u_{\parallel }$) and is also located in the middle of the cell width at ![]() $L_{\bot }/2$, but at a different height, 10 mm above the lower boundary (
$L_{\bot }/2$, but at a different height, 10 mm above the lower boundary (![]() $H/4$). Both transducers are in direct contact with the liquid metal which allows a good velocity signal quality even at low velocities.
$H/4$). Both transducers are in direct contact with the liquid metal which allows a good velocity signal quality even at low velocities.
The difference between the mean temperatures of the heated and the cooled plates is obtained from two sets of nine thermocouples, with each set located in the heated and the cooled plates, respectively. The diameter of the thermocouples is 1.5 mm and they measure the plate temperature at a 2 mm distance from the boundary layer. The temperature difference between the measuring position and the boundary layer due to heat conductivity in the copper was taken into account for the calculation of ![]() $Ra$ and
$Ra$ and ![]() $Nu$. The thermocouples are individually calibrated using a high precision thermometer to ensure accuracy better than 0.05 K.
$Nu$. The thermocouples are individually calibrated using a high precision thermometer to ensure accuracy better than 0.05 K.
Another five thermocouples measure the temperature inside the liquid metal at a distance of 3 mm below the cold plate (cf. figure 1b,c).
The convective heat transport is expressed in dimensionless form by means of the Nusselt number, ![]() $Nu=\dot {\varPhi }/\dot {\varPhi }_{cond}$. Here,
$Nu=\dot {\varPhi }/\dot {\varPhi }_{cond}$. Here, ![]() $\dot {\varPhi }_{cond}=\lambda L^2 \Delta T / H$ is the conductive heat flux, with
$\dot {\varPhi }_{cond}=\lambda L^2 \Delta T / H$ is the conductive heat flux, with ![]() $\lambda$ being the thermal conductivity of the liquid metal;
$\lambda$ being the thermal conductivity of the liquid metal; ![]() $\dot {\varPhi }=\rho c_p \dot {V} (T_{in}-T_{out})$ is the total heat flux injected at the bottom and removed from the top wall heat exchanger, whereby
$\dot {\varPhi }=\rho c_p \dot {V} (T_{in}-T_{out})$ is the total heat flux injected at the bottom and removed from the top wall heat exchanger, whereby ![]() $c_p$ is the isobaric heat capacity of water. The total heat flux is determined by the flow rate
$c_p$ is the isobaric heat capacity of water. The total heat flux is determined by the flow rate ![]() $\dot {V}$ and the temperature change
$\dot {V}$ and the temperature change ![]() $(T_{in}-T_{out})$ of the circulating water inside the hot or cold wall heat exchangers.
$(T_{in}-T_{out})$ of the circulating water inside the hot or cold wall heat exchangers.
2.2. Non-dimensional quantities and characteristic length scale
The length, velocity and time are made non-dimensional throughout this work using the width ![]() $L$ of the cell, the free-fall velocity
$L$ of the cell, the free-fall velocity ![]() $u_{ff}$, and the free-fall time
$u_{ff}$, and the free-fall time ![]() $t_{ff}=H/u_{ff}$, respectively.
$t_{ff}=H/u_{ff}$, respectively.
In contrast to the work of Vogt et al. (Reference Vogt, Ishimi, Yanagisawa, Tasaka, Sakuraba and Eckert2018a) the Chandrasekhar number was not determined with the cell height ![]() $H$ but with the distance
$H$ but with the distance ![]() $L_{\parallel }$ of the horizontal walls in the magnetic field direction. The definition of
$L_{\parallel }$ of the horizontal walls in the magnetic field direction. The definition of ![]() $Q$ using the height
$Q$ using the height ![]() $H$ goes back to the studies of Burr & Müller (Reference Burr and Müller2002), who used the same definition of the Hartmann number
$H$ goes back to the studies of Burr & Müller (Reference Burr and Müller2002), who used the same definition of the Hartmann number ![]() $Ha$ with
$Ha$ with ![]() $H$ as characteristic length for their investigations both in the vertical (Burr & Müller Reference Burr and Müller2001) and the horizontal magnetic field (Burr & Müller Reference Burr and Müller2002). In our opinion, the use of the horizontal dimension of the cell is better suited for the case of a horizontal magnetic field, since the effect of Hartmann braking scales with the dimension of the flow domain in the magnetic field direction (Müller & Bühler Reference Müller and Bühler2001; Knaepen & Moreau Reference Knaepen and Moreau2008).
$H$ as characteristic length for their investigations both in the vertical (Burr & Müller Reference Burr and Müller2001) and the horizontal magnetic field (Burr & Müller Reference Burr and Müller2002). In our opinion, the use of the horizontal dimension of the cell is better suited for the case of a horizontal magnetic field, since the effect of Hartmann braking scales with the dimension of the flow domain in the magnetic field direction (Müller & Bühler Reference Müller and Bühler2001; Knaepen & Moreau Reference Knaepen and Moreau2008).
3. Results
All results presented here were recorded after the temperature difference between the hot and the cold plates reached a constant value, and the system had attained thermal equilibrium. At low magnetic field strength, the convection at sufficiently high ![]() $Ra$ forms a large-scale circulation with a three-dimensional cellular structure that fills the entire cell (figure 2a,b,g), whereby upwelling takes place in the centre and all four corners of the vessel. A detailed description of this structure can be found in Akashi et al. (Reference Akashi, Yanagisawa, Tasaka, Vogt, Murai and Eckert2019). The large amplitude oscillation that can be seen in figure 2(a,b) is a typical feature of inertia-dominated liquid metal flows due to their low viscosity and high density (Vogt et al. Reference Vogt, Horn, Grannan and Aurnou2018b). Applying a horizontal magnetic field to such a three-dimensional flow promotes the formation of quasi-two-dimensional convection rolls that are aligned parallel to the magnetic field lines. The number of rolls formed depends on the ratio between the driving and the stabilizing force
$Ra$ forms a large-scale circulation with a three-dimensional cellular structure that fills the entire cell (figure 2a,b,g), whereby upwelling takes place in the centre and all four corners of the vessel. A detailed description of this structure can be found in Akashi et al. (Reference Akashi, Yanagisawa, Tasaka, Vogt, Murai and Eckert2019). The large amplitude oscillation that can be seen in figure 2(a,b) is a typical feature of inertia-dominated liquid metal flows due to their low viscosity and high density (Vogt et al. Reference Vogt, Horn, Grannan and Aurnou2018b). Applying a horizontal magnetic field to such a three-dimensional flow promotes the formation of quasi-two-dimensional convection rolls that are aligned parallel to the magnetic field lines. The number of rolls formed depends on the ratio between the driving and the stabilizing force ![]() $Ra/Q$ and the aspect ratio
$Ra/Q$ and the aspect ratio ![]() $\varGamma$ of the vessel (Tasaka et al. Reference Tasaka, Igaki, Yanagisawa, Vogt, Zürner and Eckert2016). Figure 2(c,d) shows an example of a convective flow field under the influence of an intermediate magnetic field strength and exhibits an unstable roll configuration. In this range, the magnetic field is not yet intense enough to produce a stable quasi-two-dimensional flow in perfection. The character of the global flow is still three-dimensional, but the magnetic field has caused a breaking of the symmetry, which characterizes the cell structure. The flow structure is dominated by the convection rolls, but their shape and orientation are still transient and subject to strong three-dimensional disturbances. Four rolls are formed in this transitional range, but these are irregular, and temporary changes to three- or five-roll configurations can occur. At higher field strength, the flow develops five counter-rotating convection rolls which are very stable in time (figure 2e,f,h). At this stage, convection has restructured into a quasi-two-dimensional flow field oriented parallel to the magnetic field direction. The symmetric but weak flow that appears along
$\varGamma$ of the vessel (Tasaka et al. Reference Tasaka, Igaki, Yanagisawa, Vogt, Zürner and Eckert2016). Figure 2(c,d) shows an example of a convective flow field under the influence of an intermediate magnetic field strength and exhibits an unstable roll configuration. In this range, the magnetic field is not yet intense enough to produce a stable quasi-two-dimensional flow in perfection. The character of the global flow is still three-dimensional, but the magnetic field has caused a breaking of the symmetry, which characterizes the cell structure. The flow structure is dominated by the convection rolls, but their shape and orientation are still transient and subject to strong three-dimensional disturbances. Four rolls are formed in this transitional range, but these are irregular, and temporary changes to three- or five-roll configurations can occur. At higher field strength, the flow develops five counter-rotating convection rolls which are very stable in time (figure 2e,f,h). At this stage, convection has restructured into a quasi-two-dimensional flow field oriented parallel to the magnetic field direction. The symmetric but weak flow that appears along ![]() $L_{\parallel }$ is evoked by the Ekman pumping that originates in the Bödewadt boundary layers, where the convection rolls meet the sidewalls (Vogt et al. Reference Vogt, Ishimi, Yanagisawa, Tasaka, Sakuraba and Eckert2018a). A weak but regular oscillation is visible in figure 2(e,f), which is due to inertial waves within the convection rolls (Yang, Vogt & Eckert Reference Yang, Vogt and Eckert2021). However, apart from these regular oscillations, the flow appears to be laminar. Based on the flow fields shown in figure 2, we distinguish here mainly between three characteristic regimes, the ‘cell structure’, where the influence of the magnetic field on the flow is negligible, the ‘unstable 3,4,5-roll’ state, where the field starts to reorganize the flow but is not strong enough to form stable roll configurations, and finally the ‘stable 5-roll’ state at higher Chandrasekhar numbers that results in the formation of stable, quasi-two-dimensional convection rolls.
$L_{\parallel }$ is evoked by the Ekman pumping that originates in the Bödewadt boundary layers, where the convection rolls meet the sidewalls (Vogt et al. Reference Vogt, Ishimi, Yanagisawa, Tasaka, Sakuraba and Eckert2018a). A weak but regular oscillation is visible in figure 2(e,f), which is due to inertial waves within the convection rolls (Yang, Vogt & Eckert Reference Yang, Vogt and Eckert2021). However, apart from these regular oscillations, the flow appears to be laminar. Based on the flow fields shown in figure 2, we distinguish here mainly between three characteristic regimes, the ‘cell structure’, where the influence of the magnetic field on the flow is negligible, the ‘unstable 3,4,5-roll’ state, where the field starts to reorganize the flow but is not strong enough to form stable roll configurations, and finally the ‘stable 5-roll’ state at higher Chandrasekhar numbers that results in the formation of stable, quasi-two-dimensional convection rolls.
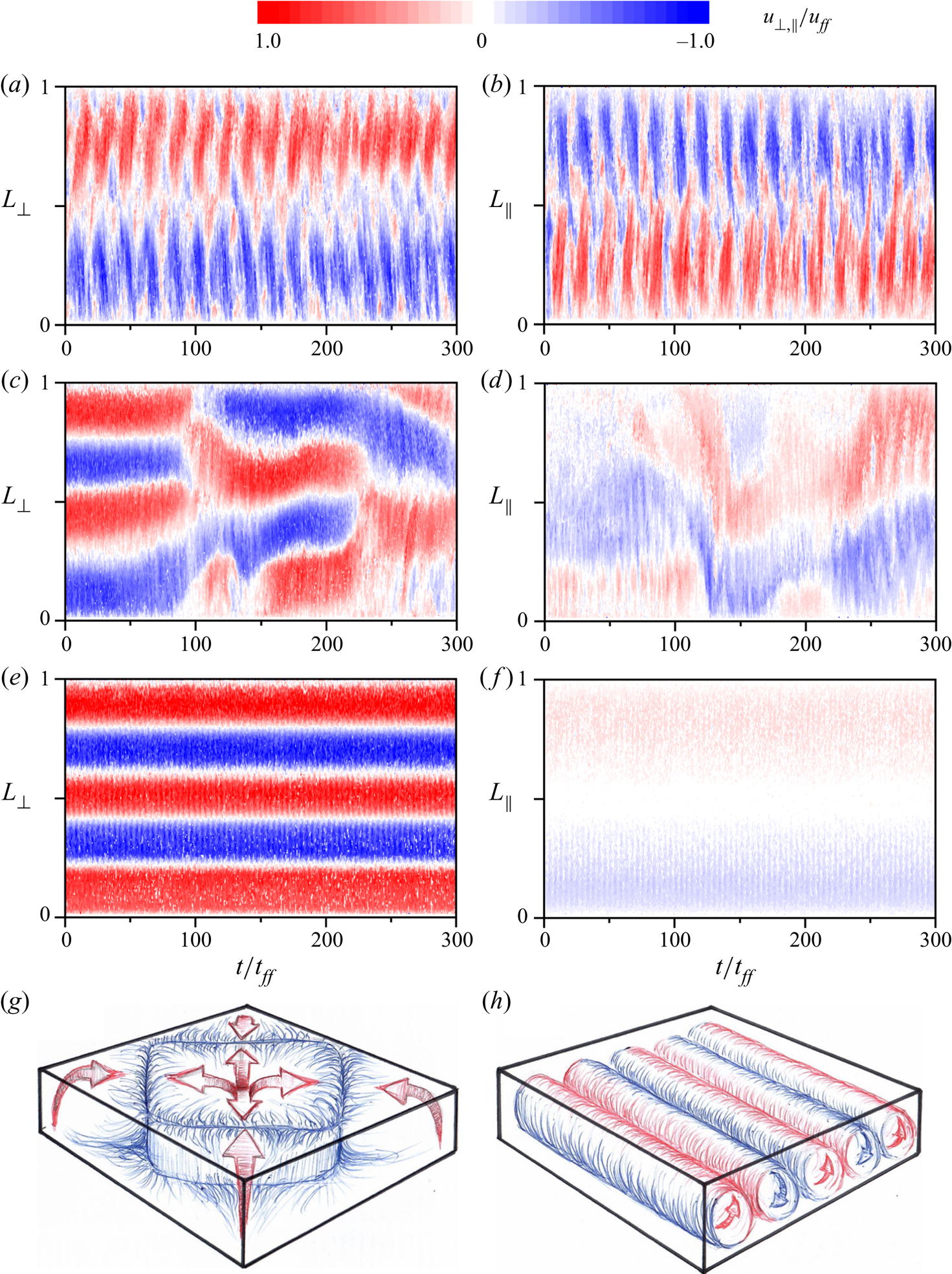
Figure 2. UDV dopplergrams: spatio-temporal distribution of the horizontal velocity measured perpendicular (a,c,e) and parallel (b,d,f) to the magnetic field direction at ![]() $Ra=2.18 \times 10^5$. The measuring lines referred to are indicated in figure 1. A positive (negative) velocity represents a flow away from (towards) the transducer. The velocities and time are non-dimensionalized using the free-fall velocity
$Ra=2.18 \times 10^5$. The measuring lines referred to are indicated in figure 1. A positive (negative) velocity represents a flow away from (towards) the transducer. The velocities and time are non-dimensionalized using the free-fall velocity ![]() $u_{ff}=\sqrt {\alpha g \Delta T H} = 21.9\ \textrm {mm}\ \textrm {s}^{-1}$ and the free-fall time
$u_{ff}=\sqrt {\alpha g \Delta T H} = 21.9\ \textrm {mm}\ \textrm {s}^{-1}$ and the free-fall time ![]() $t_{ff}=H/u_{ff}=1.8\ \textrm {s}$. The ordinate corresponds to the measuring depth along the horizontal dimensions
$t_{ff}=H/u_{ff}=1.8\ \textrm {s}$. The ordinate corresponds to the measuring depth along the horizontal dimensions ![]() $L_{\bot }$ and
$L_{\bot }$ and ![]() $L_{\parallel }$ of the container. An increase of the magnetic field strength changes the global flow structure from: (a,b) oscillating cell structure at
$L_{\parallel }$ of the container. An increase of the magnetic field strength changes the global flow structure from: (a,b) oscillating cell structure at ![]() $Q=529$, (c,d) unstable 3,4,5-roll configuration at
$Q=529$, (c,d) unstable 3,4,5-roll configuration at ![]() $Q=8.7 \times 10^4$, (e,f) stable 5-roll configuration at
$Q=8.7 \times 10^4$, (e,f) stable 5-roll configuration at ![]() $Q=3.8 \times 10^5$. (g) Schematic illustration of the cell regime and (h) the stable 5-role regime. Red areas symbolize warm, ascending fluid and blue areas symbolize colder, descending fluid.
$Q=3.8 \times 10^5$. (g) Schematic illustration of the cell regime and (h) the stable 5-role regime. Red areas symbolize warm, ascending fluid and blue areas symbolize colder, descending fluid.
Figure 3(a) shows the root-mean-square (rms) of temperature fluctuations ![]() $T_{rms}$ for all three regimes measured with thermocouple
$T_{rms}$ for all three regimes measured with thermocouple ![]() $T1$ which is under the cold plate, dipped 3 mm into the liquid metal at the cell centre. The temperature fluctuations are calculated as
$T1$ which is under the cold plate, dipped 3 mm into the liquid metal at the cell centre. The temperature fluctuations are calculated as
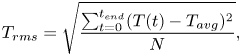 \begin{equation} T_{rms} = \sqrt{\frac{\sum_{t=0}^{t_{end}}(T(t)-T_{avg})^{2}}{N}}, \end{equation}
\begin{equation} T_{rms} = \sqrt{\frac{\sum_{t=0}^{t_{end}}(T(t)-T_{avg})^{2}}{N}}, \end{equation}
with ![]() $T_{avg} = \langle T(t)\rangle _{t}$ the average over the whole measurement and
$T_{avg} = \langle T(t)\rangle _{t}$ the average over the whole measurement and ![]() $N$ the number of measurement points. The vertical dashed lines in figure 3(b) show the boundaries between the three different flow regimes. However, this is only indicative since the actual regime boundaries depend not only on
$N$ the number of measurement points. The vertical dashed lines in figure 3(b) show the boundaries between the three different flow regimes. However, this is only indicative since the actual regime boundaries depend not only on ![]() $Q$ but also on
$Q$ but also on ![]() $Ra$. The fluctuations are strongest in the cell structure regime and the unstable 3,4,5-roll regime. The larger the
$Ra$. The fluctuations are strongest in the cell structure regime and the unstable 3,4,5-roll regime. The larger the ![]() $Ra$ number, the stronger the fluctuations. At the transition to the stable 5-roll regime, the fluctuations decrease significantly and are close to zero, which indicates that, from this point on, the position and orientation of the rolls within the convection cell are arrested by the applied magnetic field. The slight but systematic increase of the fluctuations in the stable regime is surprising at first sight, but can be explained by the occurrence of inertial waves inside the convection rolls (Yang et al. Reference Yang, Vogt and Eckert2021). Finally, at very high magnetic field strengths, these oscillations are also damped and the temperature fluctuations decrease again and approach zero. Figure 3(b) shows the cross-correlation of the different temperature sensors within the liquid metal calculated as
$Ra$ number, the stronger the fluctuations. At the transition to the stable 5-roll regime, the fluctuations decrease significantly and are close to zero, which indicates that, from this point on, the position and orientation of the rolls within the convection cell are arrested by the applied magnetic field. The slight but systematic increase of the fluctuations in the stable regime is surprising at first sight, but can be explained by the occurrence of inertial waves inside the convection rolls (Yang et al. Reference Yang, Vogt and Eckert2021). Finally, at very high magnetic field strengths, these oscillations are also damped and the temperature fluctuations decrease again and approach zero. Figure 3(b) shows the cross-correlation of the different temperature sensors within the liquid metal calculated as
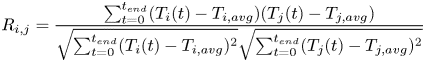 \begin{equation} R_{i,j}={\frac {\sum _{t=0}^{t_{end}}(T_{i}(t)-T_{i,avg})(T_{j}(t)-T_{j,avg})}{{\sqrt {\sum _{t=0}^{t_{end}}(T_{i}(t)-T_{i,avg})^{2}}}{\sqrt {\sum _{t=0}^{t_{end}}(T_{j}(t)-T_{j,avg})^{2}}}}}\end{equation}
\begin{equation} R_{i,j}={\frac {\sum _{t=0}^{t_{end}}(T_{i}(t)-T_{i,avg})(T_{j}(t)-T_{j,avg})}{{\sqrt {\sum _{t=0}^{t_{end}}(T_{i}(t)-T_{i,avg})^{2}}}{\sqrt {\sum _{t=0}^{t_{end}}(T_{j}(t)-T_{j,avg})^{2}}}}}\end{equation}
where ![]() $R_{i,j}$ is Pearson's correlation coefficient. In the cell structure regime, all cross-correlation coefficients are scattered around zero and indicate a negligible correlation between the different measurement points due to a complex and turbulent flow field. In the unstable roll regime, the first rolls form along the magnetic field and the cross-correlation coefficient between the corresponding adjacent sensors in the magnetic field direction increases and approaches
$R_{i,j}$ is Pearson's correlation coefficient. In the cell structure regime, all cross-correlation coefficients are scattered around zero and indicate a negligible correlation between the different measurement points due to a complex and turbulent flow field. In the unstable roll regime, the first rolls form along the magnetic field and the cross-correlation coefficient between the corresponding adjacent sensors in the magnetic field direction increases and approaches ![]() $R_{i,j} \approx 1$.
$R_{i,j} \approx 1$.
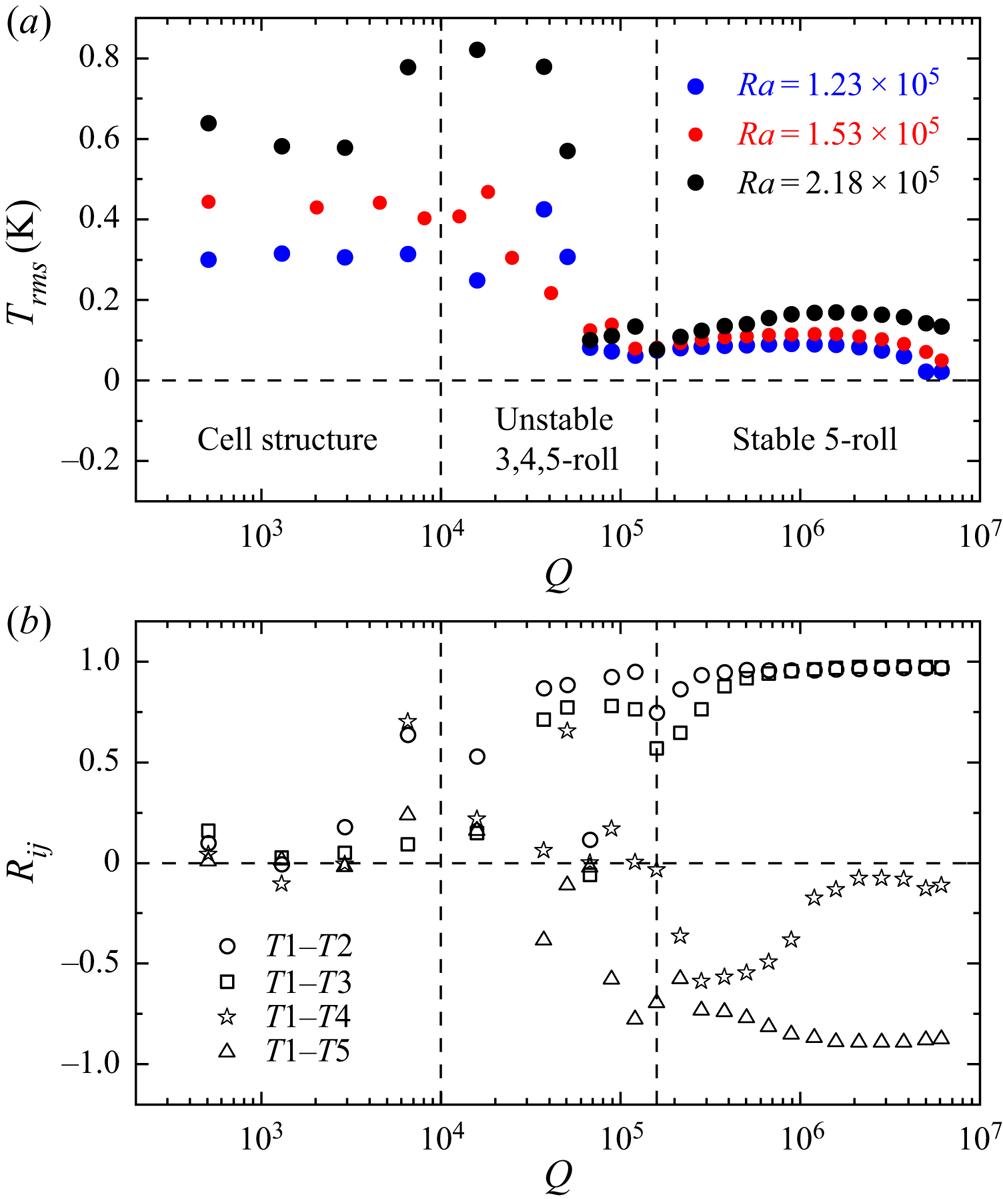
Figure 3. Liquid metal temperature measurements at a 3 mm distance from the top plate and their dependence on ![]() $Q$. (a) The rms of the temperature fluctuation of
$Q$. (a) The rms of the temperature fluctuation of ![]() $T1$ for three different
$T1$ for three different ![]() $Ra$ numbers. (b) Cross-correlation coefficient at different temperature measuring positions at
$Ra$ numbers. (b) Cross-correlation coefficient at different temperature measuring positions at ![]() $Ra = 2.18 \times 10^5$. The different symbols denote the value of the cross-correlation coefficients between corresponding thermocouples:
$Ra = 2.18 \times 10^5$. The different symbols denote the value of the cross-correlation coefficients between corresponding thermocouples: ![]() $T1$ and
$T1$ and ![]() $T2$ (circles),
$T2$ (circles), ![]() $T1$ and
$T1$ and ![]() $T3$ (squares),
$T3$ (squares), ![]() $T1$ and
$T1$ and ![]() $T4$ (stars) and
$T4$ (stars) and ![]() $T1$ and
$T1$ and ![]() $T5$ (triangles).
$T5$ (triangles).
In the stable 5-roll regime, sensors ![]() $T1$,
$T1$, ![]() $T2$ and
$T2$ and ![]() $T3$ are located along the same roll. The sensor
$T3$ are located along the same roll. The sensor ![]() $T5$ is located centrally above the neighbouring convection roll with opposite rotation direction. Sensor
$T5$ is located centrally above the neighbouring convection roll with opposite rotation direction. Sensor ![]() $T4$ is located centrally between two neighbouring convection rolls.
$T4$ is located centrally between two neighbouring convection rolls.
During transition to the stable 5-roll regime, the values for ![]() $R_{T1\text {--}T2}$ and
$R_{T1\text {--}T2}$ and ![]() $R_{T1\text {--}T3}$ decrease initially, and then approach a value of 1 again. A correlation of approximately 1 is expected as these thermocouples (
$R_{T1\text {--}T3}$ decrease initially, and then approach a value of 1 again. A correlation of approximately 1 is expected as these thermocouples (![]() $T1$,
$T1$, ![]() $T2$ and
$T2$ and ![]() $T3$) are located along the same roll. The reason for the initial decrease of the cross-correlation coefficient is that the oscillations at the beginning of the stable roll regime are still weak and three-dimensional in nature (Yang et al. Reference Yang, Vogt and Eckert2021). With increasing magnetic field strength, the three-dimensional character of the oscillations is suppressed, and from
$T3$) are located along the same roll. The reason for the initial decrease of the cross-correlation coefficient is that the oscillations at the beginning of the stable roll regime are still weak and three-dimensional in nature (Yang et al. Reference Yang, Vogt and Eckert2021). With increasing magnetic field strength, the three-dimensional character of the oscillations is suppressed, and from ![]() $Q>10^6$ onwards, only quasi-two-dimensional oscillations take place. The cross-correlation coefficient of
$Q>10^6$ onwards, only quasi-two-dimensional oscillations take place. The cross-correlation coefficient of ![]() $R_{T1\text {--}T2}$ and
$R_{T1\text {--}T2}$ and ![]() $R_{T1\text {--}T3}$ then reaches its maximum. The oscillations of neighbouring rolls take place with a phase shift of
$R_{T1\text {--}T3}$ then reaches its maximum. The oscillations of neighbouring rolls take place with a phase shift of ![]() ${\rm \pi}$. For this reason,
${\rm \pi}$. For this reason, ![]() $T5$ which is located centrally above the neighbouring roll with an opposite direction of rotation, registers a cross-correlation coefficient
$T5$ which is located centrally above the neighbouring roll with an opposite direction of rotation, registers a cross-correlation coefficient ![]() $R_{T1\text {--}T5} \approx -1$. At the measuring position
$R_{T1\text {--}T5} \approx -1$. At the measuring position ![]() $T4$ between two adjacent rolls, remaining oscillations vanish with increasing
$T4$ between two adjacent rolls, remaining oscillations vanish with increasing ![]() $Q$ and the correlation coefficient
$Q$ and the correlation coefficient ![]() $R_{T1\text {--}T4}$ approaches zero for high magnetic field strengths.
$R_{T1\text {--}T4}$ approaches zero for high magnetic field strengths.
For the case of RBC without a magnetic field, our measurements show that the heat transport properties scale as: ![]() $Nu_{{0}} = (0.166 \pm 0.014) Ra^{0.250 \pm 0.007}$, as shown in figure 4(a). This is in reasonable agreement with
$Nu_{{0}} = (0.166 \pm 0.014) Ra^{0.250 \pm 0.007}$, as shown in figure 4(a). This is in reasonable agreement with ![]() $Nu_{{0}} = 0.147 Ra^{0.257}$ measured in mercury (Rossby Reference Rossby1969) and
$Nu_{{0}} = 0.147 Ra^{0.257}$ measured in mercury (Rossby Reference Rossby1969) and ![]() $Nu_{\textit {0}} = 0.19 Ra^{0.249}$ measured in gallium (King & Aurnou Reference King and Aurnou2013). Note, that mercury, gallium and GaInSn have comparable Prandtl numbers in the range
$Nu_{\textit {0}} = 0.19 Ra^{0.249}$ measured in gallium (King & Aurnou Reference King and Aurnou2013). Note, that mercury, gallium and GaInSn have comparable Prandtl numbers in the range ![]() $Pr=0.025\text {--}0.033$. The good agreement between the measured
$Pr=0.025\text {--}0.033$. The good agreement between the measured ![]() $Nu$ numbers on the top and bottom shows that the heat loss is negligible. Figure 4(b) presents the relative deviation (
$Nu$ numbers on the top and bottom shows that the heat loss is negligible. Figure 4(b) presents the relative deviation (![]() $Nu \text {--} Nu_{{0}})/Nu_{{0}}$ for convection with an imposed magnetic field, where
$Nu \text {--} Nu_{{0}})/Nu_{{0}}$ for convection with an imposed magnetic field, where ![]() $Nu_0$ is the corresponding Nusselt number for RBC (without a magnetic field). In the case of cellular flow structures, which are the prevailing structures for
$Nu_0$ is the corresponding Nusselt number for RBC (without a magnetic field). In the case of cellular flow structures, which are the prevailing structures for ![]() $0 < Q < 1 \times 10^4$, the heat transfer does not vary remarkably with increasing
$0 < Q < 1 \times 10^4$, the heat transfer does not vary remarkably with increasing ![]() $Q$. This behaviour changes in the range
$Q$. This behaviour changes in the range ![]() $1 \times 10^4 < Q < 1.6 \times 10^5$, where the formation of unstable convection rolls proceeds with a significant increase of heat transfer. Finally, for
$1 \times 10^4 < Q < 1.6 \times 10^5$, where the formation of unstable convection rolls proceeds with a significant increase of heat transfer. Finally, for ![]() $Q>1.6 \times 10^5$,
$Q>1.6 \times 10^5$, ![]() $Nu$ reaches a maximum before the heat transfer decreases for even higher
$Nu$ reaches a maximum before the heat transfer decreases for even higher ![]() $Q$. The investigation of a wider
$Q$. The investigation of a wider ![]() $Ra$ range is not possible with our current experimental set-up. This is due to limited power range of the thermostats, and the cell height which limits Rayleigh number,
$Ra$ range is not possible with our current experimental set-up. This is due to limited power range of the thermostats, and the cell height which limits Rayleigh number, ![]() $Ra_{max} \approx 3 \times 10^5$. On the other hand, lowering
$Ra_{max} \approx 3 \times 10^5$. On the other hand, lowering ![]() $Ra \leqslant 10^5$ triggers a transition from a stable 5-roll to a 4-roll structure regime which is beyond the scope of this paper, as we focus only on the
$Ra \leqslant 10^5$ triggers a transition from a stable 5-roll to a 4-roll structure regime which is beyond the scope of this paper, as we focus only on the ![]() $Ra$ range where the stable 5-roll configuration fits well into the aspect ratio
$Ra$ range where the stable 5-roll configuration fits well into the aspect ratio ![]() $\varGamma = 5$ of the cell. Enhancement of heat transfer in a liquid metal layer due to the application of a horizontal magnetic field was also investigated by
Burr & Müller (Reference Burr and Müller2002). Temperature measurements revealed an increase of
$\varGamma = 5$ of the cell. Enhancement of heat transfer in a liquid metal layer due to the application of a horizontal magnetic field was also investigated by
Burr & Müller (Reference Burr and Müller2002). Temperature measurements revealed an increase of ![]() $Nu$ in a certain range of
$Nu$ in a certain range of ![]() $Q$. The correlation of temperature signals suggests that the enhancement of the convective heat transfer is accompanied by the existence of non-isotropic time-dependent flows. However, there are still no direct flow measurements of this phenomenon to explain the increase in convective heat transport.
$Q$. The correlation of temperature signals suggests that the enhancement of the convective heat transfer is accompanied by the existence of non-isotropic time-dependent flows. However, there are still no direct flow measurements of this phenomenon to explain the increase in convective heat transport.
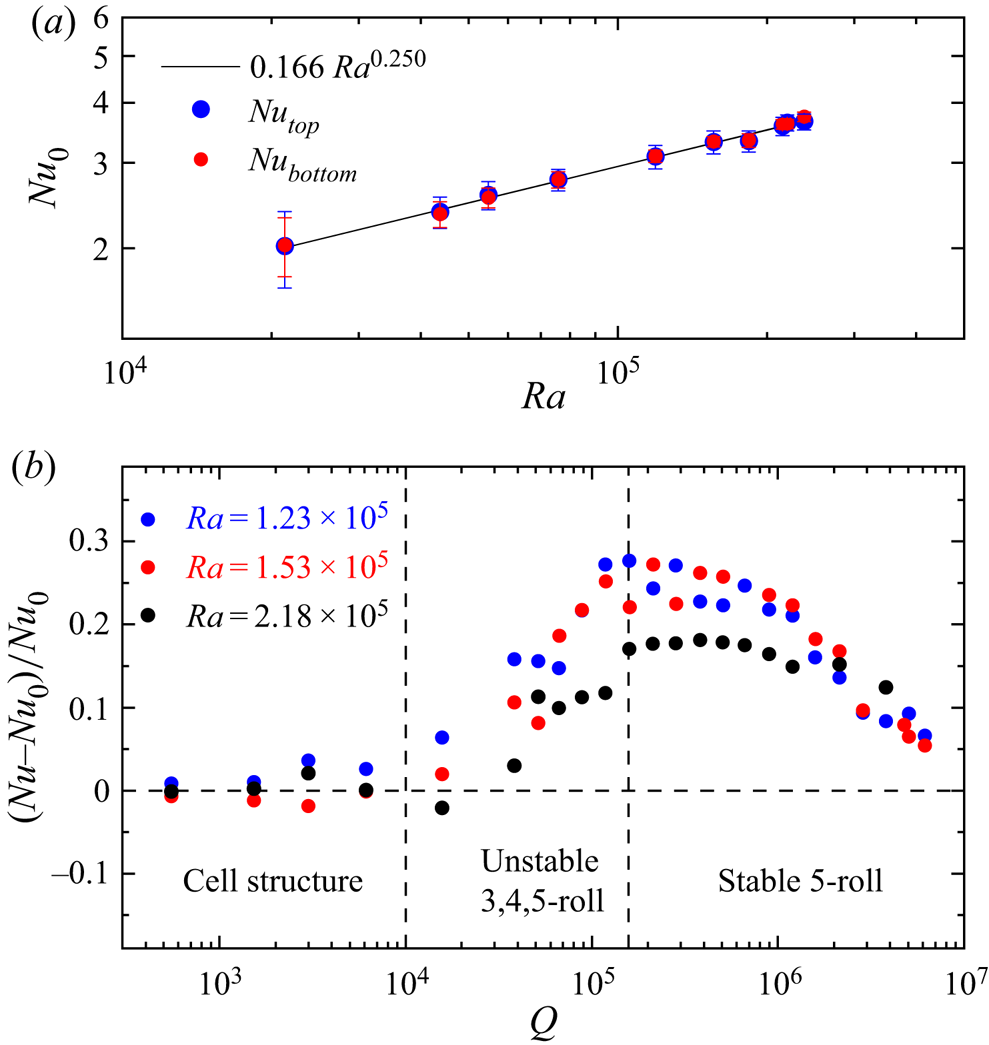
Figure 4. (a) Measured Nusselt number ![]() $Nu_{{0}}$ for convection without magnetic field. Here,
$Nu_{{0}}$ for convection without magnetic field. Here, ![]() $Nu_{top}$ and
$Nu_{top}$ and ![]() $Nu_{bottom}$ are based on the total heat flux measured at the top and bottom heat exchanger, respectively. The error bars show the measured standard deviation. (b) Relative deviations of the heat transfer from the reference state of RBC (without a magnetic field), (
$Nu_{bottom}$ are based on the total heat flux measured at the top and bottom heat exchanger, respectively. The error bars show the measured standard deviation. (b) Relative deviations of the heat transfer from the reference state of RBC (without a magnetic field), (![]() $Nu\text {--}Nu_{{0}})/Nu_{{0}}$ as a function of
$Nu\text {--}Nu_{{0}})/Nu_{{0}}$ as a function of ![]() $Q$ for three different
$Q$ for three different ![]() $Ra$ numbers. The heat transfer reaches its maximum at
$Ra$ numbers. The heat transfer reaches its maximum at ![]() $Q\approx 2.5 \times 10^5$ when the magnetic field forms stable convection rolls aligned parallel to the magnetic field.
$Q\approx 2.5 \times 10^5$ when the magnetic field forms stable convection rolls aligned parallel to the magnetic field.
Based on velocity measurements, we analyse the ![]() $Q$ dependence of the amplitude of the velocity components perpendicular
$Q$ dependence of the amplitude of the velocity components perpendicular ![]() $\hat {u}_{\bot }$ and parallel
$\hat {u}_{\bot }$ and parallel ![]() $\hat {u}_{\parallel }$ to the magnetic field as shown in figure 5. The maximum velocity values
$\hat {u}_{\parallel }$ to the magnetic field as shown in figure 5. The maximum velocity values ![]() $\hat {u}_i$ for figure 5 were determined as follows: for each measurement, a velocity threshold was defined, such that 95 % of the velocity values of a measurement are below the threshold value. This approach provides very reliable values for the vast majority of measurements. Only at the largest
$\hat {u}_i$ for figure 5 were determined as follows: for each measurement, a velocity threshold was defined, such that 95 % of the velocity values of a measurement are below the threshold value. This approach provides very reliable values for the vast majority of measurements. Only at the largest ![]() $Q$ and the associated very low velocities
$Q$ and the associated very low velocities ![]() $\hat {u}_{\parallel }$, is the signal-to-noise ratio of the velocity measurements not sufficient to apply this method. For these measurements,
$\hat {u}_{\parallel }$, is the signal-to-noise ratio of the velocity measurements not sufficient to apply this method. For these measurements, ![]() $\hat {u}_{\parallel }$ was determined from the time-averaged quasi-stationary velocity profile.
$\hat {u}_{\parallel }$ was determined from the time-averaged quasi-stationary velocity profile.
Figure 5. (a) The ![]() $Q$ dependence of the
$Q$ dependence of the ![]() $\hat {u}_{\bot }$ and
$\hat {u}_{\bot }$ and ![]() $\hat {u}_{\parallel }$ velocity components and the corresponding Reynolds number
$\hat {u}_{\parallel }$ velocity components and the corresponding Reynolds number ![]() $Re = \hat {u}_{i} H / \nu$. (b) The
$Re = \hat {u}_{i} H / \nu$. (b) The ![]() $Q$ dependence of the normalized horizontal velocity amplitudes for three different
$Q$ dependence of the normalized horizontal velocity amplitudes for three different ![]() $Ra$ numbers. The field-normal velocity amplitude increases from
$Ra$ numbers. The field-normal velocity amplitude increases from ![]() $\hat {u}_{\bot }/u_{ff}\approx 0.7$ for cellular flow structures (
$\hat {u}_{\bot }/u_{ff}\approx 0.7$ for cellular flow structures (![]() $Q<1 \times 10^4$) to
$Q<1 \times 10^4$) to ![]() ${O}(u_{ff})$ in the stable 5-roll regime (
${O}(u_{ff})$ in the stable 5-roll regime (![]() $Q\approx 2.5 \times 10^5$). The diverging branches of
$Q\approx 2.5 \times 10^5$). The diverging branches of ![]() $\hat {u}_{\parallel }$ and
$\hat {u}_{\parallel }$ and ![]() $\hat {u}_{\bot }$ start with the transition from a cellular flow structure to magnetic field aligned convection rolls at
$\hat {u}_{\bot }$ start with the transition from a cellular flow structure to magnetic field aligned convection rolls at ![]() $Q>1 \times 10^4$.
$Q>1 \times 10^4$.
The flow velocities, and as such the ![]() $Re$ number, increases with
$Re$ number, increases with ![]() $Ra$ in all three regimes. As for the heat transfer, the velocity components of the cell structure do not significantly change for
$Ra$ in all three regimes. As for the heat transfer, the velocity components of the cell structure do not significantly change for ![]() $Q<1 \times 10^4$. Both velocity components,
$Q<1 \times 10^4$. Both velocity components, ![]() $\hat {u}_{\bot }$ and
$\hat {u}_{\bot }$ and ![]() $\hat {u}_{\parallel }$, are of the same order of magnitude and reach an amplitude of approximately
$\hat {u}_{\parallel }$, are of the same order of magnitude and reach an amplitude of approximately ![]() $\hat {u}_{\bot }/u_{ff} \approx 0.7$, which is an expected velocity value for low
$\hat {u}_{\bot }/u_{ff} \approx 0.7$, which is an expected velocity value for low ![]() $Pr$ thermal convection in this
$Pr$ thermal convection in this ![]() $Ra$ range (Vogt et al. Reference Vogt, Horn, Grannan and Aurnou2018b; Zürner et al. Reference Zürner, Schindler, Vogt, Eckert and Schumacher2019). For
$Ra$ range (Vogt et al. Reference Vogt, Horn, Grannan and Aurnou2018b; Zürner et al. Reference Zürner, Schindler, Vogt, Eckert and Schumacher2019). For ![]() $Q>1 \times 10^4$, the development of the unstable 3,4,5-roll state goes along with a separation of the velocity components. The increase of
$Q>1 \times 10^4$, the development of the unstable 3,4,5-roll state goes along with a separation of the velocity components. The increase of ![]() $\hat {u}_{\bot }$ and the decrease of
$\hat {u}_{\bot }$ and the decrease of ![]() $\hat {u}_{\parallel }$ indicate that the flow field starts to become quasi-two-dimensional. The relatively large scatter of the velocity data in this regime is caused by the transient flow behaviour with frequent reversals of the flow direction. At
$\hat {u}_{\parallel }$ indicate that the flow field starts to become quasi-two-dimensional. The relatively large scatter of the velocity data in this regime is caused by the transient flow behaviour with frequent reversals of the flow direction. At ![]() $Q > 1.6 \times 10^5$, the flow structure changes into the stable 5-roll state, which remains the dominant flow structure for at least one decade of
$Q > 1.6 \times 10^5$, the flow structure changes into the stable 5-roll state, which remains the dominant flow structure for at least one decade of ![]() $Q$ numbers. The small scattering of the measured velocity amplitudes in this regime reflects the stable characteristic of this flow configuration. The velocity component parallel to the magnetic field
$Q$ numbers. The small scattering of the measured velocity amplitudes in this regime reflects the stable characteristic of this flow configuration. The velocity component parallel to the magnetic field ![]() $\hat {u}_{\parallel }$ decreases monotonically for higher
$\hat {u}_{\parallel }$ decreases monotonically for higher ![]() $Q$ while
$Q$ while ![]() $\hat {u}_{\bot }$ reaches a maximum around
$\hat {u}_{\bot }$ reaches a maximum around ![]() $Q \approx 2.5 \times 10^5$, where the velocity amplitudes reach the theoretical free-fall limit
$Q \approx 2.5 \times 10^5$, where the velocity amplitudes reach the theoretical free-fall limit ![]() $u_{ff}$. The normalization of the velocity amplitude with the free-fall velocity yields good conformity for the different
$u_{ff}$. The normalization of the velocity amplitude with the free-fall velocity yields good conformity for the different ![]() $Ra$.
$Ra$.
4. Discussion
We have demonstrated that the rearrangement of a three-dimensional thermal convection flow into a quasi-two-dimensional flow field, due to an applied static magnetic field, results in significantly increased heat and momentum transport. The convection forms five counter-rotating rolls, whereby the diameter of the rolls corresponds to the height of the fluid layer and the number of rolls results from the aspect ratio ![]() $\varGamma = 5$ of the vessel. The preferred orientation of the rolls implies that momentum oriented parallel to the magnetic field is redirected in the direction perpendicular to the field. Therefore,
$\varGamma = 5$ of the vessel. The preferred orientation of the rolls implies that momentum oriented parallel to the magnetic field is redirected in the direction perpendicular to the field. Therefore, ![]() $\hat {u}_{\parallel }$ decreases while
$\hat {u}_{\parallel }$ decreases while ![]() $\hat {u}_{\bot }$ increases. In addition, the intensity of fluctuations in the temperature and velocity fields decreases and the stabilized convection rolls appear laminar and quasi-stationary.
$\hat {u}_{\bot }$ increases. In addition, the intensity of fluctuations in the temperature and velocity fields decreases and the stabilized convection rolls appear laminar and quasi-stationary.
The vertical velocity component ![]() $u_z$ is responsible for convective heat flux, but this component was not directly measured in the experiment. However, our measurements show a fully three-dimensional flow in the cell structure regime wherein the three velocity components are of similar amplitude. It can therefore be assumed that the velocity components in this regime are as follows:
$u_z$ is responsible for convective heat flux, but this component was not directly measured in the experiment. However, our measurements show a fully three-dimensional flow in the cell structure regime wherein the three velocity components are of similar amplitude. It can therefore be assumed that the velocity components in this regime are as follows: ![]() $u_z \approx u_{\bot } \approx u_{\parallel } \approx 0.7 u_{ff}$. By contrast, in the quasi-two-dimensional, stable 5-roll regime, the flow component parallel to the magnetic field was measured to be significantly weaker compared to the flow component perpendicular to the magnetic field. These experimental results, in conjunction with the prevailing topology of the flow structure, and the requirement imposed by continuity indicate that the following relation would hold for the velocity components at the optimal state of the stable 5-roll regime:
$u_z \approx u_{\bot } \approx u_{\parallel } \approx 0.7 u_{ff}$. By contrast, in the quasi-two-dimensional, stable 5-roll regime, the flow component parallel to the magnetic field was measured to be significantly weaker compared to the flow component perpendicular to the magnetic field. These experimental results, in conjunction with the prevailing topology of the flow structure, and the requirement imposed by continuity indicate that the following relation would hold for the velocity components at the optimal state of the stable 5-roll regime: ![]() $u_z \approx u_{\bot } \approx u_{ff}$.
$u_z \approx u_{\bot } \approx u_{ff}$.
In classical RBC in fluids with moderate Prandtl numbers, such as water or air, the flow velocities are well below the free-fall limit and never exceed ![]() $u_{max}/u_{ff} \leqslant 0.2$ (Niemela & Sreenivasan Reference Niemela and Sreenivasan2003). Our results show unequivocally that the flow has a predisposition to reorient itself perpendicular to the magnetic field, which allows it to attain the optimal state wherein the fluid parcel traverses with the maximum possible velocity, the free-fall velocity. Consequently, the vigour of the convective flow in such a state is intense, leading to an enhancement of the heat flux. Further increase of the Lorentz force or
$u_{max}/u_{ff} \leqslant 0.2$ (Niemela & Sreenivasan Reference Niemela and Sreenivasan2003). Our results show unequivocally that the flow has a predisposition to reorient itself perpendicular to the magnetic field, which allows it to attain the optimal state wherein the fluid parcel traverses with the maximum possible velocity, the free-fall velocity. Consequently, the vigour of the convective flow in such a state is intense, leading to an enhancement of the heat flux. Further increase of the Lorentz force or ![]() $Q$, beyond the optimum state yields reduced convective transport due to the increasing dominance of the Hartmann braking in the lateral boundary layers perpendicular to the magnetic field (Vogt et al. Reference Vogt, Ishimi, Yanagisawa, Tasaka, Sakuraba and Eckert2018a; Yang et al. Reference Yang, Vogt and Eckert2021). In an infinite fluid layer, the Hartmann braking for an ideal two-dimensional flow structure aligned with the magnetic field direction would disappear since the characteristic Hartmann damping time scale
$Q$, beyond the optimum state yields reduced convective transport due to the increasing dominance of the Hartmann braking in the lateral boundary layers perpendicular to the magnetic field (Vogt et al. Reference Vogt, Ishimi, Yanagisawa, Tasaka, Sakuraba and Eckert2018a; Yang et al. Reference Yang, Vogt and Eckert2021). In an infinite fluid layer, the Hartmann braking for an ideal two-dimensional flow structure aligned with the magnetic field direction would disappear since the characteristic Hartmann damping time scale ![]() $\tau _{HB} = \sqrt {{\rho L^2}/{\sigma \nu B^2}}$ shows a linear dependence on the distance
$\tau _{HB} = \sqrt {{\rho L^2}/{\sigma \nu B^2}}$ shows a linear dependence on the distance ![]() $L$ between the Hartmann walls (Sommeria & Moreau Reference Sommeria and Moreau1982).
$L$ between the Hartmann walls (Sommeria & Moreau Reference Sommeria and Moreau1982).
In previous works (Chong et al. Reference Chong, Yang, Huang, Zhong, Stevens, Verzicco, Lohse and Xia2017; Lim et al. Reference Lim, Chong, Ding and Xia2019), the increase in Nusselt number was explained as a result of increased coherency of the flow structures, which act as the main carrier for the heat transport. Moreover, the authors concluded that the maximum heat flux is achieved when the thermal and viscous boundary layers reach the same thickness. Our results differ in several respects from the studies mentioned above. First, the low ![]() $Pr \ll 1$ implies that the viscous boundary layer is always nested well inside the much thicker thermal boundary layer. A cross-over of the boundary layer thicknesses is, therefore, not expected in very low Prandtl number fluids such as liquid metals. Second, in our case, not only the heat flux, but also the momentum transport perpendicular to the magnetic field, is increased. And finally, the low
$Pr \ll 1$ implies that the viscous boundary layer is always nested well inside the much thicker thermal boundary layer. A cross-over of the boundary layer thicknesses is, therefore, not expected in very low Prandtl number fluids such as liquid metals. Second, in our case, not only the heat flux, but also the momentum transport perpendicular to the magnetic field, is increased. And finally, the low ![]() $Pr$ of liquid metals implies that the Péclet number
$Pr$ of liquid metals implies that the Péclet number ![]() $Pe = Re \,Pr$ remains low when compared to moderate
$Pe = Re \,Pr$ remains low when compared to moderate ![]() $Pr$ flows at a comparable turbulence level (Vogt et al. Reference Vogt, Horn, Grannan and Aurnou2018b). The consequence is a pronounced coherence in the flow field even without the influence of the magnetic field.
$Pr$ flows at a comparable turbulence level (Vogt et al. Reference Vogt, Horn, Grannan and Aurnou2018b). The consequence is a pronounced coherence in the flow field even without the influence of the magnetic field.
The application of a horizontal magnetic field supports an increase in the coherence of the flow pattern in a particularly striking way by transforming unsteady three-dimensional flows into stable two-dimensional structures. In this context, it is very interesting to point out that the application of small magnetic fields in the range of the three-dimensional flow ![]() $(Q < 10^4)$ does not show any measurable effects for the heat and momentum transport. From magnetohydrodynamic (MHD) turbulence, it is known that the transition from isotropic to anisotropic turbulence starts at values of the magnetic interaction parameter
$(Q < 10^4)$ does not show any measurable effects for the heat and momentum transport. From magnetohydrodynamic (MHD) turbulence, it is known that the transition from isotropic to anisotropic turbulence starts at values of the magnetic interaction parameter ![]() $N= Q/Re \approx 1$ (Davidson Reference Davidson1995; Eckert et al. Reference Eckert, Gerbeth, Witke and Langenbrunner2001). When crossing this threshold, the effect of the Lorentz force sets in, which prevents three-dimensional structures from absorbing the energy supplied by the thermal driving. Instead, the development of quasi-two-dimensional structures is promoted. The interaction parameter reaches values of approximately 5 at the transition from the cell structure to the unstable roll regimes. The cell structure is completely three-dimensional and an amplification of the flow by the Lorentz force is not plausible in view of the described mechanism. Only with the emergence of the convection rolls are the quasi-two-dimensional structures available, into which energy can be transferred. Accordingly, our measurements show a simultaneous increase of both momentum and heat transport in the regime of unstable roll structures.
$N= Q/Re \approx 1$ (Davidson Reference Davidson1995; Eckert et al. Reference Eckert, Gerbeth, Witke and Langenbrunner2001). When crossing this threshold, the effect of the Lorentz force sets in, which prevents three-dimensional structures from absorbing the energy supplied by the thermal driving. Instead, the development of quasi-two-dimensional structures is promoted. The interaction parameter reaches values of approximately 5 at the transition from the cell structure to the unstable roll regimes. The cell structure is completely three-dimensional and an amplification of the flow by the Lorentz force is not plausible in view of the described mechanism. Only with the emergence of the convection rolls are the quasi-two-dimensional structures available, into which energy can be transferred. Accordingly, our measurements show a simultaneous increase of both momentum and heat transport in the regime of unstable roll structures.
In conclusion, we have shown how a stabilizing, static magnetic field can significantly alter the flow dynamics such that the free-fall velocity is attained by the flow structure, resulting in enhanced heat and momentum transport in thermal convection. These trends remain a consistent feature for all the Rayleigh numbers investigated. It is likely that the optimum state for the heat and momentum transport does not solely depend on ![]() $Q$, but also on a combination of
$Q$, but also on a combination of ![]() $Q$,
$Q$, ![]() $Ra$ and
$Ra$ and ![]() $\varGamma$. Further investigation of this phenomenon with other combinations of parameters would therefore be desirable.
$\varGamma$. Further investigation of this phenomenon with other combinations of parameters would therefore be desirable.
Acknowledgements
The authors thank S. Singh, M. Akashi, J. Aurnou, S. Horn, T. Yanagisawa, Y. Tasaka and S. Su for fruitful discussions.
Funding
This work is supported by the Priority Programme SPP 1881 Turbulent Superstructures of the Deutsche Forschungsgemeinschaft (DFG) under the grant VO 2331/3. T.V. and F.S. also thank the DFG for the support under the grant VO 2331/1. The contribution of J.C.Y. in this project is financially supported by CSC (China Scholarship Council).
Declaration of interests
The authors report no conflict of interest.
Author contributions
T.V. and J.C.Y. contributed equally to this work and should be considered joint first authors. T.V. and S.E. planned and designed research; T.V., J.C.Y. and F.S. performed research; T.V., J.C.Y., F.S. and S.E. analysed data; T.V., J.C.Y., F.S. and S.E. wrote the paper.