Article contents
Force acting on a square cylinder fixed in a free-surface channel flow
Published online by Cambridge University Press: 04 September 2014
Abstract
We describe an experimental study of the forces acting on a square cylinder (of width 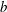 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}b$ ) which occupies 10–40 % of a channel (of width
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}b$ ) which occupies 10–40 % of a channel (of width 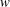 $w$ ), fixed in a free-surface channel flow. The force experienced by the obstacle depends critically on the Froude number upstream of the obstacle,
$w$ ), fixed in a free-surface channel flow. The force experienced by the obstacle depends critically on the Froude number upstream of the obstacle, 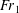 ${\mathit{Fr}}_1$ (depth
${\mathit{Fr}}_1$ (depth 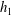 $h_1$ ), which sets the downstream Froude number,
$h_1$ ), which sets the downstream Froude number, 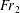 ${\mathit{Fr}}_2$ (depth
${\mathit{Fr}}_2$ (depth 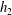 $h_2$ ). When
$h_2$ ). When 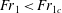 ${\mathit{Fr}}_1<{\mathit{Fr}}_{1c}$ , where
${\mathit{Fr}}_1<{\mathit{Fr}}_{1c}$ , where 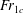 ${\mathit{Fr}}_{1c}$ is a critical Froude number, the flow is subcritical upstream and downstream of the obstacle. The drag effect tends to decrease or increase the water depth downstream or upstream of the obstacle, respectively. The force is form drag caused by an attached wake and scales as
${\mathit{Fr}}_{1c}$ is a critical Froude number, the flow is subcritical upstream and downstream of the obstacle. The drag effect tends to decrease or increase the water depth downstream or upstream of the obstacle, respectively. The force is form drag caused by an attached wake and scales as 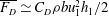 $\overline{F_{D}}\simeq C_D \rho b u_1^2 h_1/2$ , where
$\overline{F_{D}}\simeq C_D \rho b u_1^2 h_1/2$ , where 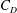 $C_D$ is a drag coefficient and
$C_D$ is a drag coefficient and 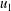 $u_1$ is the upstream flow speed. The empirically determined drag coefficient is strongly influenced by blocking, and its variation follows the trend
$u_1$ is the upstream flow speed. The empirically determined drag coefficient is strongly influenced by blocking, and its variation follows the trend 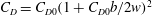 $C_D=C_{D0}(1+C_{D0}b/2w)^2$ , where
$C_D=C_{D0}(1+C_{D0}b/2w)^2$ , where 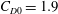 $C_{D0}=1.9$ corresponds to the drag coefficient of a square cylinder in an unblocked turbulent flow. The r.m.s. lift force is approximately 10–40 % of the mean drag force and is generated by vortex shedding from the obstacle. When
$C_{D0}=1.9$ corresponds to the drag coefficient of a square cylinder in an unblocked turbulent flow. The r.m.s. lift force is approximately 10–40 % of the mean drag force and is generated by vortex shedding from the obstacle. When 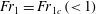 ${\mathit{Fr}}_1={\mathit{Fr}}_{1c}\, (<1)$ , the flow is choked and adjusts by generating a hydraulic jump downstream of the obstacle. The drag force scales as
${\mathit{Fr}}_1={\mathit{Fr}}_{1c}\, (<1)$ , the flow is choked and adjusts by generating a hydraulic jump downstream of the obstacle. The drag force scales as 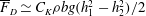 $\overline{F}_D\simeq C_K \rho b g (h_1^2-h_2^2)/2$ , where experimentally we find
$\overline{F}_D\simeq C_K \rho b g (h_1^2-h_2^2)/2$ , where experimentally we find 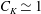 $C_K\simeq 1$ . The r.m.s. lift force is significantly smaller than the mean drag force. A consistent model is developed to explain the transitional behaviour by using a semi-empirical form of the drag force that combines form and hydrostatic components. The mean drag force scales as
$C_K\simeq 1$ . The r.m.s. lift force is significantly smaller than the mean drag force. A consistent model is developed to explain the transitional behaviour by using a semi-empirical form of the drag force that combines form and hydrostatic components. The mean drag force scales as 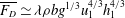 $\overline{F_{D}}\simeq \lambda \rho b g^{1/3} u_1^{4/3} h_1^{4/3}$ , where
$\overline{F_{D}}\simeq \lambda \rho b g^{1/3} u_1^{4/3} h_1^{4/3}$ , where 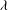 $\lambda $ is a function of
$\lambda $ is a function of 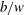 $b/w$ and
$b/w$ and 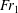 ${\mathit{Fr}}_1$ . For a choked flow,
${\mathit{Fr}}_1$ . For a choked flow, 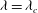 $\lambda =\lambda _c$ is a function of blocking (
$\lambda =\lambda _c$ is a function of blocking ( 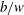 $b/w$ ). For small blocking fractions,
$b/w$ ). For small blocking fractions, 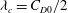 $\lambda _c= C_{D0}/2$ . In the choked flow regime, the largest contribution to the total drag force comes from the form-drag component.
$\lambda _c= C_{D0}/2$ . In the choked flow regime, the largest contribution to the total drag force comes from the form-drag component.
JFM classification
Information
- Type
- Papers
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/3.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © 2014 Cambridge University Press
References
- 79
- Cited by

