No CrossRef data available.
Published online by Cambridge University Press: 31 August 2017
The aspect ratio dependence of the electroconvection phenomenon in a suspended nematic liquid crystal film with a rectangular boundary is investigated. Two-dimensional global stability analysis is carried out on the coupled electrohydrodynamic system to calculate the instability boundary of the phenomenon for different aspect ratios. The calculated critical 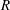 $R$ number (Rayleigh-like number) shows a rapidly decreasing trend in the low-aspect-ratio region (roughly
$R$ number (Rayleigh-like number) shows a rapidly decreasing trend in the low-aspect-ratio region (roughly 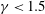 $\unicode[STIX]{x1D6FE}<1.5$, where
$\unicode[STIX]{x1D6FE}<1.5$, where 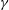 $\unicode[STIX]{x1D6FE}$ is defined as the aspect ratio of the film), and then the variation becomes slow until
$\unicode[STIX]{x1D6FE}$ is defined as the aspect ratio of the film), and then the variation becomes slow until 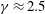 $\unicode[STIX]{x1D6FE}\approx 2.5$, where the critical
$\unicode[STIX]{x1D6FE}\approx 2.5$, where the critical 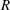 $R$ number starts to increase slightly. Convective patterns of liquid films with different aspect ratios are also obtained from stability analysis and validated by particle image velocimetry measurement.
$R$ number starts to increase slightly. Convective patterns of liquid films with different aspect ratios are also obtained from stability analysis and validated by particle image velocimetry measurement.