Article contents
Analysis of the hypersonic cross-flow instability with experimental wavenumber distributions
Published online by Cambridge University Press: 28 November 2019
Abstract
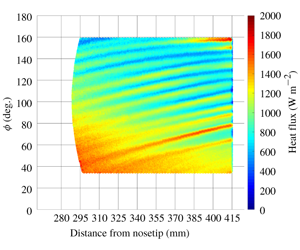
Stationary cross-flow vortex N-factors were calculated over the surface of a yawed circular cone using computationally predicted and experimentally observed wavenumber distributions. Surface heat-flux data were obtained on a  $7^{\circ }$ half-angle circular cone to investigate the behaviour of the stationary waves at different angles of attack and Reynolds numbers at Mach 6 under quiet-flow conditions in the Boeing/AFOSR Mach-6 Quiet Tunnel at Purdue University. A wavelet analysis was conducted on the experimental surface heat-flux data to construct a spatial mapping of the local largest amplitude wavenumbers of the stationary cross-flow waves, which were between 40 and 80 per circumference. Significant axial and azimuthal variation was observed. The results from the wavelet analysis were used to inform the stability analysis. The computed integration marching directions demonstrated very good agreement with the experimentally observed paths. N-factors were first calculated by integrating the local amplification rate corresponding to the most amplified experimental wavenumbers. The calculations were repeated based on non-dimensional computationally varying wavenumber ratios, which were dimensionalized by the experimental data. The computed N-factors showed good agreement between the two techniques. N-factors were also computed using the computationally predicted most unstable wavenumbers. The results showed decreased agreement with the other two cases, suggesting that this assumption does not properly model the cross-flow transition process.
$7^{\circ }$ half-angle circular cone to investigate the behaviour of the stationary waves at different angles of attack and Reynolds numbers at Mach 6 under quiet-flow conditions in the Boeing/AFOSR Mach-6 Quiet Tunnel at Purdue University. A wavelet analysis was conducted on the experimental surface heat-flux data to construct a spatial mapping of the local largest amplitude wavenumbers of the stationary cross-flow waves, which were between 40 and 80 per circumference. Significant axial and azimuthal variation was observed. The results from the wavelet analysis were used to inform the stability analysis. The computed integration marching directions demonstrated very good agreement with the experimentally observed paths. N-factors were first calculated by integrating the local amplification rate corresponding to the most amplified experimental wavenumbers. The calculations were repeated based on non-dimensional computationally varying wavenumber ratios, which were dimensionalized by the experimental data. The computed N-factors showed good agreement between the two techniques. N-factors were also computed using the computationally predicted most unstable wavenumbers. The results showed decreased agreement with the other two cases, suggesting that this assumption does not properly model the cross-flow transition process.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 16
- Cited by

