Published online by Cambridge University Press: 04 March 2014
Full numerical simulations of the Navier–Stokes equations for four cases of vertically falling liquid films with three-dimensional surface waves have been performed. Flow conditions are based on several previous experimental studies where the streamwise and spanwise wavelengths were imposed, which we exploit by simulating periodic wave segments. The considered flows are laminar but approach conditions at which intermittent wave-induced turbulence has been observed elsewhere. Working liquids range from water to silicone oil and cover a large interval of the Kapitza number (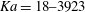 $\textit {Ka}=18\mbox{--}3923$), which relates capillary to viscous forces. Simulations were performed on a supercomputer, using a finite-volume code and the volume of fluid and continuum surface force methods to account for the multiphase nature of the flow. Our results show that surface waves, consisting of large horseshoe-shaped wave humps concentrating most of the liquid and preceded by capillary ripples on a thin residual film, segregate the flow field into two regions: an inertia-dominated one in the large humps, where the local Reynolds number is up to five times larger than its mean value, and a visco-capillary region, where capillary and/or viscous forces dominate. In the inertial region, an intricate structure of different-scale vortices arises, which is more complicated than film thickness variations there suggest. Conversely, the flow in the visco-capillary region of large-
$\textit {Ka}=18\mbox{--}3923$), which relates capillary to viscous forces. Simulations were performed on a supercomputer, using a finite-volume code and the volume of fluid and continuum surface force methods to account for the multiphase nature of the flow. Our results show that surface waves, consisting of large horseshoe-shaped wave humps concentrating most of the liquid and preceded by capillary ripples on a thin residual film, segregate the flow field into two regions: an inertia-dominated one in the large humps, where the local Reynolds number is up to five times larger than its mean value, and a visco-capillary region, where capillary and/or viscous forces dominate. In the inertial region, an intricate structure of different-scale vortices arises, which is more complicated than film thickness variations there suggest. Conversely, the flow in the visco-capillary region of large-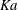 $\textit {Ka} $ fluids is entirely governed by the local free-surface curvature through the action of capillary forces, which impose the pressure distribution in the liquid film. This results in flow separation zones underneath the capillary troughs and a spanwise cellular flow pattern in the region of capillary wave interference. In some cases, capillary waves bridge the large horseshoe humps in the spanwise direction, coupling the two aforementioned regions and leading the flow to oscillate between three- and two-dimensional wave patterns. This persists over long times, as we show by simulations with the low-dimensional model of Scheid et al. (J. Fluid Mech., vol. 562, 2006, pp. 183–222) after satisfactory comparison with our direct simulations at short times. The governing mechanism is connected to the bridging capillary waves, which drain liquid from the horseshoe humps, decreasing their amplitude and wave speed and causing them to retract in the streamwise direction. Overall, it is observed that spanwise flow structures (not accounted for in two-dimensional investigations) are particularly complex due to the absence of gravity in this direction.
$\textit {Ka} $ fluids is entirely governed by the local free-surface curvature through the action of capillary forces, which impose the pressure distribution in the liquid film. This results in flow separation zones underneath the capillary troughs and a spanwise cellular flow pattern in the region of capillary wave interference. In some cases, capillary waves bridge the large horseshoe humps in the spanwise direction, coupling the two aforementioned regions and leading the flow to oscillate between three- and two-dimensional wave patterns. This persists over long times, as we show by simulations with the low-dimensional model of Scheid et al. (J. Fluid Mech., vol. 562, 2006, pp. 183–222) after satisfactory comparison with our direct simulations at short times. The governing mechanism is connected to the bridging capillary waves, which drain liquid from the horseshoe humps, decreasing their amplitude and wave speed and causing them to retract in the streamwise direction. Overall, it is observed that spanwise flow structures (not accounted for in two-dimensional investigations) are particularly complex due to the absence of gravity in this direction.
DNS of case 1 (first line in tables 1-3 of manuscript): Re tgt=41, ftgt=19 Hz, Ka =3923, L=20 mm, W =10 mm. Time evolution of the velocity field projected onto a horizontal slice at the position of the trailing main wave hump.
DNS of case 1 (first line in tables 1-3 of manuscript): Retgt=41, ftgt=19 Hz, Ka=3923, L=20 mm, W=10 mm. Time evolution of the liquid-gas interface.
WRIBL model simulation of case 1 (first line in tables 1-3 of manuscript): Re tgt=41, f tgt=19 Hz, Ka. =3923, L=20 mm, W =10 mm. Time evolution of the liquid-gas interface.
DNS of case 2 (second line in tables 1-3 of manuscript): Retgt=59, f tgt=17 Hz, Ka =3923, L=25 mm, W =10 mm. Time evolution of the velocity field projected onto a horizontal slice at the position of the trailing main wave hump.
DNS of case 2 (second line in tables 1-3 of manuscript): Retgt=59, ftgt=17 Hz, Ka=3923, L=25 mm, W=10 mm. Time evolution of the liquid-gas interface.
WRIBL model simulation of case 2 (second line in tables 1-3 of manuscript): Re tgt=59, f tgt=17 Hz, Ka =3923, L=25 mm, W =10 mm. Time evolution of the liquid-gas interface.
DNS of case 3 (third line in tables 1-3 of manuscript): Retgt=15, ftgt=16 Hz, Ka=509.5, L=20.7 mm, W=10.35 mm. Time evolution of the liquid-gas interface.
WRIBL model simulation of case 3 (third line in tables 1-3 of manuscript) on a domain spanning two wavelengths in streamwise and spanwise directions: Re tgt=15, f tgt=16 Hz, Ka =509.5, L=20.7 mm, W=10.35 mm. Time evolution of film thickness contours (white: wave hump; black: wave trough).
WRIBL model simulation of case 3 (third line in tables 1-3 of manuscript): Re tgt=15, f tgt=16 Hz, Ka =509.5, L=20.7 mm, W =10.35 mm. Time evolution of the liquid-gas interface.
DNS of case 4 (fourth line in tables 1-3 of manuscript): Retgt=6, ftgt=17 Hz, Ka=17.8, L=22 mm, W=15 mm. Time evolution of the liquid-gas interface.
WRIBL model simulation of case 4 (fourth line in tables 1-3 of manuscript) on a domain spanning two wavelengths in streamwise and spanwise directions: Re tgt=6, f tgt=17 Hz, Ka=17.8, L=22 mm, W=15 mm. Time evolution of film thickness contours (white: wave hump; black: wave trough).