Article contents
Temporal stability analysis of jets of lobed geometry
Published online by Cambridge University Press: 05 December 2018
Abstract
A two-dimensional temporal incompressible stability analysis is performed for lobed jets. The jet base flow is assumed to be parallel and of a vortex-sheet type. The eigenfunctions of this simplified stability problem are expanded using the eigenfunctions of a round jet. The original problem is then formulated as an innovative matrix eigenvalue problem, which can be solved in a very robust and efficient manner. The results show that the lobed geometry changes both the convection velocity and temporal growth rate of the instability waves. However, different modes are affected differently. In particular, mode 0 is not sensitive to the geometry changes, whereas modes of higher orders can be changed significantly. The changes become more pronounced as the number of lobes 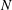 $N$ and the penetration ratio
$N$ and the penetration ratio  $\unicode[STIX]{x1D716}$ increase. Moreover, the lobed geometry can cause a previously degenerate eigenvalue (
$\unicode[STIX]{x1D716}$ increase. Moreover, the lobed geometry can cause a previously degenerate eigenvalue (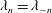 $\unicode[STIX]{x1D706}_{n}=\unicode[STIX]{x1D706}_{-n}$) to become non-degenerate (
$\unicode[STIX]{x1D706}_{n}=\unicode[STIX]{x1D706}_{-n}$) to become non-degenerate (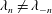 $\unicode[STIX]{x1D706}_{n}\neq \unicode[STIX]{x1D706}_{-n}$) and lead to opposite changes to the stability characteristics of the corresponding symmetric (
$\unicode[STIX]{x1D706}_{n}\neq \unicode[STIX]{x1D706}_{-n}$) and lead to opposite changes to the stability characteristics of the corresponding symmetric ( $n$) and antisymmetric (
$n$) and antisymmetric (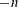 $-n$) modes. It is also shown that each eigenmode changes its shape in response to the lobes of the vortex sheet, and the degeneracy of an eigenvalue occurs when the vortex sheet has more symmetric planes than the corresponding mode shape (including both symmetric and antisymmetric planes). The new approach developed in this paper can be used to study the stability characteristics of jets of other arbitrary geometries in a robust and efficient manner.
$-n$) modes. It is also shown that each eigenmode changes its shape in response to the lobes of the vortex sheet, and the degeneracy of an eigenvalue occurs when the vortex sheet has more symmetric planes than the corresponding mode shape (including both symmetric and antisymmetric planes). The new approach developed in this paper can be used to study the stability characteristics of jets of other arbitrary geometries in a robust and efficient manner.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 4
- Cited by

