Published online by Cambridge University Press: 10 August 2023
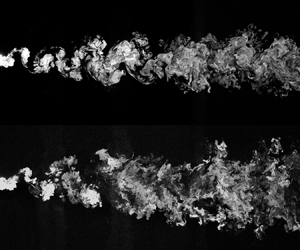
This study aims to examine the spatial evolution of the geometrical features of the turbulent/turbulent interface (TTI) in a cylinder wake. The wake is exposed to various turbulent backgrounds in which the turbulence intensity and the integral length scale are varied independently, and comparisons to a turbulent/non-turbulent interface (TNTI) are drawn. The turbulent wake was marked with a high Schmidt number ( $Sc$) scalar, and a planar laser induced fluorescence experiment was carried out to capture the interface between the wake and the ambient flow from
$Sc$) scalar, and a planar laser induced fluorescence experiment was carried out to capture the interface between the wake and the ambient flow from  $x/d = 5$ to 40, where
$x/d = 5$ to 40, where  $x$ is the streamwise coordinate from the centre of the cylinder, and
$x$ is the streamwise coordinate from the centre of the cylinder, and  $d$ is the cylinder's diameter. It is found that the TTI generally spreads faster towards the ambient flow than the TNTI. A transition region of the interfaces’ spreading is found at
$d$ is the cylinder's diameter. It is found that the TTI generally spreads faster towards the ambient flow than the TNTI. A transition region of the interfaces’ spreading is found at  $x/d \approx 15$, after which the interfaces propagate at a slower rate than previously (upstream), and the mean interface positions of both the TNTI and TTI scale with the local wake half-width. The locations of both the TNTI and TTI have non-Gaussian probability density functions (PDFs) in the near wake because of the influence of the large-scale coherent motions present within the flow. Further downstream, after the large-scale coherent motions have dissipated, the TNTI position PDF does become Gaussian. For the first time, we explore the spatial variation of the ‘roughness’ of the TTI, quantified via the fractal dimension, from near field to far field. The length scale in the background flow has a profound effect on the TTI fractal dimension in the near wake, whilst the turbulence intensity becomes important only for the fractal dimension farther downstream.
$x/d \approx 15$, after which the interfaces propagate at a slower rate than previously (upstream), and the mean interface positions of both the TNTI and TTI scale with the local wake half-width. The locations of both the TNTI and TTI have non-Gaussian probability density functions (PDFs) in the near wake because of the influence of the large-scale coherent motions present within the flow. Further downstream, after the large-scale coherent motions have dissipated, the TNTI position PDF does become Gaussian. For the first time, we explore the spatial variation of the ‘roughness’ of the TTI, quantified via the fractal dimension, from near field to far field. The length scale in the background flow has a profound effect on the TTI fractal dimension in the near wake, whilst the turbulence intensity becomes important only for the fractal dimension farther downstream.