Published online by Cambridge University Press: 07 July 2021
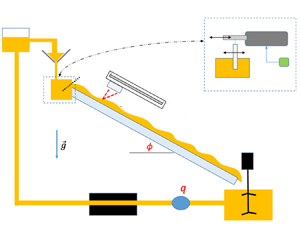
We study experimentally the primary instability of a visco-plastic film flow down an inclined plane. The experimental set-up is a channel with a varying slope angle, in which a permanent flow of a Herschel–Bulkley fluid (carbopol or kaolin) is established. Controlled perturbations are imposed at the entrance of the channel to generate surface waves, and their downstream evolution is observed with a laser sensor system measuring the local fluid thickness. Growth rates and cutoff frequencies are obtained after processing the thickness signal, and experimental critical Reynolds and Bingham numbers are deduced. We find that the experimental stability map obtained is well described by the pseudo-plug model of Balmforth & Liu (J. Fluid Mech., vol, 519, 2004, pp. 33–54), a model obtained after neglecting the film thickness compared with its length. This is not the case for dispersion effects (growth rates, cutoff frequencies, phase speeds), for which a more accurate model is needed.