Article contents
Homogenization-based design of microstructured membranes: wake flows past permeable shells
Published online by Cambridge University Press: 29 September 2021
Abstract
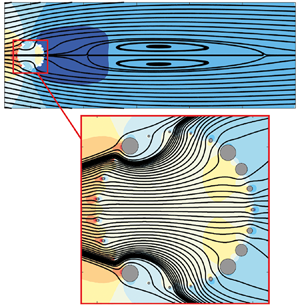
A formal framework to characterize and control/optimize the flow past permeable membranes by means of a homogenization approach is proposed and applied to the wake flow past a permeable cylindrical shell. From a macroscopic viewpoint, a Navier-like effective stress jump condition is employed to model the presence of the membrane, in which the normal and tangential velocities at the membrane are respectively proportional to the so-called filtrability and slip numbers multiplied by the stresses. Regarding the particular geometry considered here, a characterization of the steady flow for several combinations of constant filtrability and slip numbers shows that the flow morphology is dominantly influenced by the filtrability and exhibits a recirculation region that moves downstream of the body and eventually disappears as this number increases. A linear stability analysis further shows the suppression of vortex shedding as long as large values of the filtrability number are employed. In the control/optimization phase, specific objectives for the macroscopic flow are formulated by adjoint methods. A homogenization-based inverse procedure is proposed to obtain the optimal constrained microscopic geometry from macroscopic objectives, which accounts for fast variations of the filtrability and slip profiles along the membrane. As a test case for the proposed design methodology, a cylindrical membrane is designed to maximize the resulting drag coefficient.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 16
- Cited by


