Article contents
Flow kinematics and air entrainment under laboratory spilling breaking waves
Published online by Cambridge University Press: 08 November 2019
Abstract
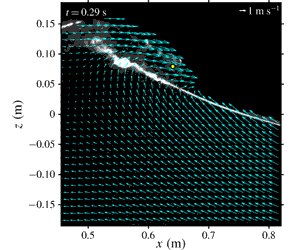
Laboratory measurements of velocity fields and void fraction under spilling breaking waves are presented. Modified particle image velocimetry was used to quantify the flow kinematics and turbulence while fibre optic reflectometry was used to quantify the breaking-induced air entrainment inside the aerated region of the spilling breakers. The measurements confirmed that the ratio of the local energy flux and the local energy density sharply increases and exceeds the threshold value of 0.85 near the onset of breaking. Based on the measured velocity fields, the maximum horizontal velocity reached  $1.1C$ at the onset of breaking, with
$1.1C$ at the onset of breaking, with  $C$ being the phase speed of the primary breaking wave. The maximum horizontal velocity then reached
$C$ being the phase speed of the primary breaking wave. The maximum horizontal velocity then reached  $1.5C$ at approximately one-quarter of a wave period after the onset of breaking. The results also confirmed that the wavelet-educed turbulence length scale estimates are comparable to the previously reported values with different wave parameters, suggesting that the dependence of the size of energy-containing eddies on the physical scales of the breaking waves is insignificant. The measured void fraction showed a similarity profile although the measurement locations span one wavelength. The mean kinetic energy, turbulent kinetic energy, potential energy and total energy were quantified with and without the void fraction being accounted for. Results show near 60 % and 40 % overestimates of the kinetic energy and the potential energy if the void fraction is not considered. After correcting the density variation due to air entrainment, the total energy dissipated following an exponential decay, with 43 % and 65 % energy being dissipated at one and two wavelengths downstream from the breaking point, respectively. The equipartition assumption was found to be applicable before and during the entire breaking process in the present spilling breakers.
$1.5C$ at approximately one-quarter of a wave period after the onset of breaking. The results also confirmed that the wavelet-educed turbulence length scale estimates are comparable to the previously reported values with different wave parameters, suggesting that the dependence of the size of energy-containing eddies on the physical scales of the breaking waves is insignificant. The measured void fraction showed a similarity profile although the measurement locations span one wavelength. The mean kinetic energy, turbulent kinetic energy, potential energy and total energy were quantified with and without the void fraction being accounted for. Results show near 60 % and 40 % overestimates of the kinetic energy and the potential energy if the void fraction is not considered. After correcting the density variation due to air entrainment, the total energy dissipated following an exponential decay, with 43 % and 65 % energy being dissipated at one and two wavelengths downstream from the breaking point, respectively. The equipartition assumption was found to be applicable before and during the entire breaking process in the present spilling breakers.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 19
- Cited by

