Article contents
Drag forces on sparsely packed cube arrays
Published online by Cambridge University Press: 18 October 2019
Abstract
Flow over aligned and staggered cube arrays is a classic model problem for rough-wall turbulent boundary layers. Earlier studies of this model problem mainly looked at rough surfaces with a moderate coverage density, i.e. 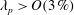 $\unicode[STIX]{x1D706}_{p}>O(3\,\%)$, where
$\unicode[STIX]{x1D706}_{p}>O(3\,\%)$, where 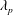 $\unicode[STIX]{x1D706}_{p}$ is the surface coverage density and is defined to be the ratio between the area occupied by the roughness and the total ground area. At lower surface coverage densities, i.e.
$\unicode[STIX]{x1D706}_{p}$ is the surface coverage density and is defined to be the ratio between the area occupied by the roughness and the total ground area. At lower surface coverage densities, i.e. 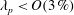 $\unicode[STIX]{x1D706}_{p}<O(3\,\%)$, it is conventionally thought that cubical roughness acts like isolated roughness elements; and that the single-cube drag coefficient, i.e.
$\unicode[STIX]{x1D706}_{p}<O(3\,\%)$, it is conventionally thought that cubical roughness acts like isolated roughness elements; and that the single-cube drag coefficient, i.e. 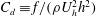 $C_{d}\equiv f/(\unicode[STIX]{x1D70C}U_{h}^{2}h^{2})$, equals
$C_{d}\equiv f/(\unicode[STIX]{x1D70C}U_{h}^{2}h^{2})$, equals 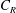 $C_{R}$. Here,
$C_{R}$. Here, 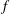 $f$ is the drag force on one cubical roughness element,
$f$ is the drag force on one cubical roughness element, 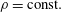 $\unicode[STIX]{x1D70C}=\text{const.}$ is the fluid density,
$\unicode[STIX]{x1D70C}=\text{const.}$ is the fluid density, 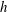 $h$ is the height of the cube,
$h$ is the height of the cube,  $U_{h}$ is the spatially and temporally averaged wind speed at the cube height, and
$U_{h}$ is the spatially and temporally averaged wind speed at the cube height, and 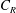 $C_{R}$ is the drag coefficient of an isolated cube. In this work, we conduct large-eddy simulations and direct numerical simulations of flow over wall-mounted cubes with very low surface coverage densities, i.e.
$C_{R}$ is the drag coefficient of an isolated cube. In this work, we conduct large-eddy simulations and direct numerical simulations of flow over wall-mounted cubes with very low surface coverage densities, i.e. 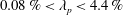 $0.08\,\%<\unicode[STIX]{x1D706}_{p}<4.4\,\%$. The large-eddy simulations are at nominally infinite Reynolds numbers. The results challenge the conventional thinking, and we show that, at very low surface coverage densities, the single-cube drag coefficient may increase as a function of
$0.08\,\%<\unicode[STIX]{x1D706}_{p}<4.4\,\%$. The large-eddy simulations are at nominally infinite Reynolds numbers. The results challenge the conventional thinking, and we show that, at very low surface coverage densities, the single-cube drag coefficient may increase as a function of 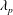 $\unicode[STIX]{x1D706}_{p}$. Our analysis suggests that this behaviour may be attributed to secondary turbulent flows. Secondary turbulent flows are often found above spanwise-heterogeneous roughness. Although the roughness considered in this work is nominally homogeneous, the secondary flows in our simulations are very similar to those observed above spanwise-heterogeneous surface roughness. These secondary vortices redistribute the fluid momentum in the outer layer, leading to high-momentum pathways above the wall-mounted cubes and low-momentum pathways at the two sides of the wall-mounted cubes. As a result, the spatially and temporally averaged wind speed at the cube height, i.e.
$\unicode[STIX]{x1D706}_{p}$. Our analysis suggests that this behaviour may be attributed to secondary turbulent flows. Secondary turbulent flows are often found above spanwise-heterogeneous roughness. Although the roughness considered in this work is nominally homogeneous, the secondary flows in our simulations are very similar to those observed above spanwise-heterogeneous surface roughness. These secondary vortices redistribute the fluid momentum in the outer layer, leading to high-momentum pathways above the wall-mounted cubes and low-momentum pathways at the two sides of the wall-mounted cubes. As a result, the spatially and temporally averaged wind speed at the cube height, i.e. 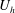 $U_{h}$, is an underestimate of the incoming flow to the cubes, which in turn leads to a large drag coefficient
$U_{h}$, is an underestimate of the incoming flow to the cubes, which in turn leads to a large drag coefficient 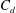 $C_{d}$.
$C_{d}$.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 39
- Cited by

