Article contents
Density-ratio effects on the capture of suspended particles in aquatic systems
Published online by Cambridge University Press: 15 October 2015
Abstract
Particle capture, whereby suspended particles contact and adhere to a solid surface (a ‘collector’), is important in a range of environmental processes, including suspension feeding by corals and ‘filtering’ by aquatic vegetation. Although aquatic particles are often considered as perfect tracers when estimating capture efficiency, the particle density ratio ( 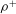 ${\it\rho}^{+}$ ) – the ratio of the particle density to the fluid density – can significantly affect capture. In this paper, we use a numerical analysis of particle trajectories to quantify the influence of
${\it\rho}^{+}$ ) – the ratio of the particle density to the fluid density – can significantly affect capture. In this paper, we use a numerical analysis of particle trajectories to quantify the influence of 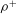 ${\it\rho}^{+}$ on particle capture by circular collectors in a parameter space relevant to aquatic systems. As it is generally believed that inertia augments the capture efficiency when the Stokes number (
${\it\rho}^{+}$ on particle capture by circular collectors in a parameter space relevant to aquatic systems. As it is generally believed that inertia augments the capture efficiency when the Stokes number ( 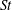 $\mathit{St}$ ) of the particles exceeds a critical value, we first estimate the critical Stokes number for aquatic-type particles and demonstrate its dependence on both
$\mathit{St}$ ) of the particles exceeds a critical value, we first estimate the critical Stokes number for aquatic-type particles and demonstrate its dependence on both 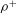 ${\it\rho}^{+}$ and the Reynolds number (
${\it\rho}^{+}$ and the Reynolds number ( 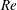 $\mathit{Re}$ ). Second, we analyse how efficiently circular collectors can capture neutrally buoyant (
$\mathit{Re}$ ). Second, we analyse how efficiently circular collectors can capture neutrally buoyant ( 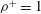 ${\it\rho}^{+}=1$ ), sediment-type (
${\it\rho}^{+}=1$ ), sediment-type ( 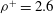 ${\it\rho}^{+}=2.6$ ) and weakly buoyant (
${\it\rho}^{+}=2.6$ ) and weakly buoyant ( 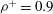 ${\it\rho}^{+}=0.9$ ) aquatic particles. Our analysis shows that, for
${\it\rho}^{+}=0.9$ ) aquatic particles. Our analysis shows that, for 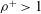 ${\it\rho}^{+}>1$ , inertia can either augment or diminish capture efficiency, and inertial effects appear well before the critical Stokes number is reached. The role of particle inertia is maximised at Stokes numbers above the critical value and, for sediment-type particles, can result in as much as a fourfold increase in the rate of capture relative to perfect tracers of the same size. Similar but opposite effects are observed for weakly buoyant particles, where capture efficiency can decrease by 60 % relative to the capture of perfect tracers.
${\it\rho}^{+}>1$ , inertia can either augment or diminish capture efficiency, and inertial effects appear well before the critical Stokes number is reached. The role of particle inertia is maximised at Stokes numbers above the critical value and, for sediment-type particles, can result in as much as a fourfold increase in the rate of capture relative to perfect tracers of the same size. Similar but opposite effects are observed for weakly buoyant particles, where capture efficiency can decrease by 60 % relative to the capture of perfect tracers.
Information
- Type
- Papers
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 20
- Cited by


