Published online by Cambridge University Press: 20 June 2007
In [Progress Math.233 (2005)], David suggested the existence of a new type of global minimizers for the Mumford-Shah functional in $\mathbf{R}^3$ 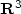 . The singular set of such a new minimizer belongs to a three parameters family of sets $(0<\delta_1,\delta_2,\delta_3<\pi)$
. The singular set of such a new minimizer belongs to a three parameters family of sets $(0<\delta_1,\delta_2,\delta_3<\pi)$ 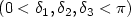 . We first derive necessary conditions satisfied by global minimizers of this family. Then we are led to study the first eigenvectors of the Laplace-Beltrami operator with Neumann boundary conditions on subdomains of $\mathbf{S}^2$
. We first derive necessary conditions satisfied by global minimizers of this family. Then we are led to study the first eigenvectors of the Laplace-Beltrami operator with Neumann boundary conditions on subdomains of $\mathbf{S}^2$ 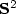 with three reentrant corners. The necessary conditions are constraints on the eigenvalue and on the ratios between the three singular coefficients of the associated eigenvector. We use numerical methods (Singular Functions Method and Moussaoui's extraction formula) to compute the eigenvalues and the singular coefficients. We conclude that there is no $(\delta_1,\delta_2,\delta_3)$
with three reentrant corners. The necessary conditions are constraints on the eigenvalue and on the ratios between the three singular coefficients of the associated eigenvector. We use numerical methods (Singular Functions Method and Moussaoui's extraction formula) to compute the eigenvalues and the singular coefficients. We conclude that there is no $(\delta_1,\delta_2,\delta_3)$ 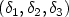 for which the necessary conditions are satisfied and this shows that the hypothesis was wrong.
for which the necessary conditions are satisfied and this shows that the hypothesis was wrong.