Article contents
Strongly aperiodic SFTs on generalized Baumslag–Solitar groups
Published online by Cambridge University Press: 20 June 2023
Abstract
We look at constructions of aperiodic subshifts of finite type (SFTs) on fundamental groups of graph of groups. In particular, we prove that all generalized Baumslag-Solitar groups (GBS) admit a strongly aperiodic SFT. Our proof is based on a structural theorem by Whyte and on two constructions of strongly aperiodic SFTs on 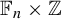 $\mathbb {F}_n\times \mathbb {Z}$ and
$\mathbb {F}_n\times \mathbb {Z}$ and 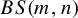 $BS(m,n)$ of our own. Our two constructions rely on a path-folding technique that lifts an SFT on
$BS(m,n)$ of our own. Our two constructions rely on a path-folding technique that lifts an SFT on 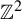 $\mathbb {Z}^2$ inside an SFT on
$\mathbb {Z}^2$ inside an SFT on 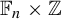 $\mathbb {F}_n\times \mathbb {Z}$ or an SFT on the hyperbolic plane inside an SFT on
$\mathbb {F}_n\times \mathbb {Z}$ or an SFT on the hyperbolic plane inside an SFT on 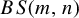 $BS(m,n)$. In the case of
$BS(m,n)$. In the case of 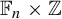 $\mathbb {F}_n\times \mathbb {Z}$, the path folding technique also preserves minimality, so that we get minimal strongly aperiodic SFTs on unimodular GBS groups.
$\mathbb {F}_n\times \mathbb {Z}$, the path folding technique also preserves minimality, so that we get minimal strongly aperiodic SFTs on unimodular GBS groups.
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
- 2
- Cited by


