No CrossRef data available.
Article contents
Scale recurrence lemma and dimension formula for Cantor sets in the complex plane
Published online by Cambridge University Press: 25 March 2024
Abstract
We prove a multidimensional conformal version of the scale recurrence lemma of Moreira and Yoccoz [Stable intersections of regular Cantor sets with large Hausdorff dimensions. Ann. of Math. (2) 154(1) (2001), 45–96] for Cantor sets in the complex plane. We then use this new recurrence lemma, together with Moreira’s ideas in [Geometric properties of images of Cartesian products of regular Cantor sets by differentiable real maps. Math. Z. 303 (2023), 3], to prove that under the right hypothesis for the Cantor sets  $K_1,\ldots ,K_n$ and the function
$K_1,\ldots ,K_n$ and the function 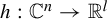 $h:\mathbb {C}^{n}\to \mathbb {R}^{l}$, the following formula holds:
$h:\mathbb {C}^{n}\to \mathbb {R}^{l}$, the following formula holds: 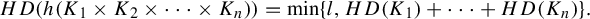 $$ \begin{align*}HD(h(K_1\times K_2 \times \cdots\times K_n))=\min \{l,HD(K_1)+\cdots+HD(K_n)\}.\end{align*} $$
$$ \begin{align*}HD(h(K_1\times K_2 \times \cdots\times K_n))=\min \{l,HD(K_1)+\cdots+HD(K_n)\}.\end{align*} $$
MSC classification
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press


