No CrossRef data available.
Article contents
Attractors associated to a family of hyperbolic 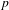 $p$ -adic plane automorphisms
$p$ -adic plane automorphisms
Part of:
Dynamical systems with hyperbolic behavior
Topological dynamics
Algebraic number theory: local and $p$-adic fields
Complex dynamical systems
Arithmetic and non-Archimedean dynamical systems
Published online by Cambridge University Press: 20 February 2020
Abstract
We consider a certain two-parameter family of automorphisms of the affine plane over a complete, locally compact non-Archimedean field. Each of these automorphisms admits a chaotic attractor on which it is topologically conjugate to a full two-sided shift map, and the attractor supports a unit Borel measure which describes the distribution of the forward orbit of Haar-almost all points in the basin of attraction. We also compute the Hausdorff dimension of the attractor, which is non-integral.
Keywords
MSC classification
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s) 2020. Published by Cambridge University Press
References
Allen, K., DeMark, D. and Petsche, C.. Non-Archimedean Hénon maps, attractors, and horseshoes. Res. Number Theory
4 (2018), Art. 5, 30 pp.Google Scholar
Benedetto, R., Briend, J.-Y. and Perdry, H.. Dynamique des polynômes quadratiques sur les corps locaux. J. Théor. Nombres Bordeaux
19 (2007), 325–336.CrossRefGoogle Scholar
Benedicks, M. and Carleson, L.. The dynamics of the Hénon map. Ann. of Math. (2)
133 (1991), 73–169.CrossRefGoogle Scholar
Devaney, R.. An Introduction to Chaotic Dynamical Systems, 2nd edn. Addison-Wesley, Redwood City, CA, 1989.Google Scholar
Devaney, R. and Nitecki, Z.. Shift automorphisms in the Hénon mapping. Comm. Math. Phys.
67 (1979), 137–146.CrossRefGoogle Scholar
Folland, G. B.. Real Analysis: Modern Techniques and Their Applications
(Pure and Applied Mathematics)
, 2nd edn. John Wiley, New York, 1999.Google Scholar
Hénon, M.. A two-dimensional mapping with a strange attractor. Comm. Math. Phys.
50 (1976), 69–77.CrossRefGoogle Scholar
Smale, S.. Differentiable dynamical systems. Bull. Amer. Math. Soc.
73 (1967), 747–817.CrossRefGoogle Scholar
Walters, P.. An Introduction to Ergodic Theory
(Graduate Texts in Mathematics, 79)
. Springer, New York, 1982.CrossRefGoogle Scholar
Woodcock, C. F. and Smart, N. P..
p-adic chaos and random number generation. Exp. Math.
7 (1998), 333–342.CrossRefGoogle Scholar
Young, L.-S.. What are SRB measures, and which dynamical systems have them?
J. Stat. Phys.
108 (2002), 733–754.CrossRefGoogle Scholar


