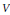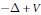Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kondratiev, Vladimir
Maz'ya, Vladimir
and
Shubin, Mikhail
2009.
Gauge Optimization and Spectral Properties of Magnetic Schrödinger Operators.
Communications in Partial Differential Equations,
Vol. 34,
Issue. 10,
p.
1127.
Kim, Daehong
and
Matsuura, Masakuni
2020.
On a scattering length for additive functionals and spectrum of fractional Laplacian with a non‐local perturbation.
Mathematische Nachrichten,
Vol. 293,
Issue. 2,
p.
327.
Zelenko, Leonid
2021.
Conditions for Discreteness of the Spectrum to Schrödinger Operator Via Non-increasing Rearrangement, Lagrangian Relaxation and Perturbations.
Integral Equations and Operator Theory,
Vol. 93,
Issue. 3,