Published online by Cambridge University Press: 20 November 2018
An integral domain 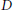 $D$ with identity is condensed (resp., strongly condensed) if for each pair of ideals
$D$ with identity is condensed (resp., strongly condensed) if for each pair of ideals 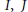 $I,\,J$ of
$I,\,J$ of 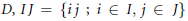 $D,\,IJ\,=\,\{ij\,;\,i\,\in I,j\in J\,\}$ (resp.,
$D,\,IJ\,=\,\{ij\,;\,i\,\in I,j\in J\,\}$ (resp., 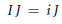 $IJ=iJ$ for some
$IJ=iJ$ for some 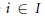 $i\,\in \,I$ or
$i\,\in \,I$ or 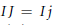 $IJ\,=Ij$ for some
$IJ\,=Ij$ for some 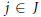 $j\,\in \,J$). We show that for a Noetherian domain
$j\,\in \,J$). We show that for a Noetherian domain 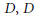 $D,\,D$ is condensed if and only if
$D,\,D$ is condensed if and only if 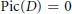 $\text{Pic}\left( D \right)\,=0$ and
$\text{Pic}\left( D \right)\,=0$ and 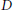 $D$ is locally condensed, while a local domain is strongly condensed if and only if it has the two-generator property. An integrally closed domain
$D$ is locally condensed, while a local domain is strongly condensed if and only if it has the two-generator property. An integrally closed domain 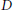 $D$ is strongly condensed if and only if
$D$ is strongly condensed if and only if 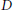 $D$ is a Bézout generalized Dedekind domain with at most one maximal ideal of height greater than one. We give a number of equivalencies for a local domain with finite integral closure to be strongly condensed. Finally, we show that for a field extension
$D$ is a Bézout generalized Dedekind domain with at most one maximal ideal of height greater than one. We give a number of equivalencies for a local domain with finite integral closure to be strongly condensed. Finally, we show that for a field extension 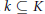 $k\,\subseteq K$, the domain
$k\,\subseteq K$, the domain 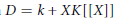 $D=\,k+XK[[X]]$ is condensed if and only if
$D=\,k+XK[[X]]$ is condensed if and only if 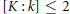 $[K:k]\,\le \,2$ or
$[K:k]\,\le \,2$ or 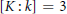 $[K:k]\,=\,3$ and each degree-two polynomial in
$[K:k]\,=\,3$ and each degree-two polynomial in 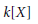 $k[X]$ splits over
$k[X]$ splits over 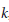 $k$, while
$k$, while 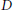 $D$ is strongly condensed if and only if
$D$ is strongly condensed if and only if 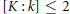 $[K:k]\,\le \,2$.
$[K:k]\,\le \,2$.