No CrossRef data available.
Article contents
On the Littlewood Problem Modulo a Prime
Published online by Cambridge University Press: 20 November 2018
Abstract
Let 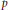 $p$ be a prime, and let
$p$ be a prime, and let 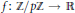 $f:\mathbb{Z}/p\mathbb{Z}\to \mathbb{R}$ be a function with
$f:\mathbb{Z}/p\mathbb{Z}\to \mathbb{R}$ be a function with 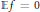 $\mathbb{E}f=0$ and
$\mathbb{E}f=0$ and  $||\hat{f}|{{|}_{1}}\le 1$ . Then
$||\hat{f}|{{|}_{1}}\le 1$ . Then 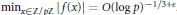 ${{\min }_{x\in \mathbb{Z}/p\mathbb{Z}}}|f\left( x \right)|=O{{\left( \log p \right)}^{-1/3+\in }}$ . One should think of
${{\min }_{x\in \mathbb{Z}/p\mathbb{Z}}}|f\left( x \right)|=O{{\left( \log p \right)}^{-1/3+\in }}$ . One should think of 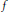 $f$ as being “approximately continuous”; our result is then an “approximate intermediate value theorem”.
$f$ as being “approximately continuous”; our result is then an “approximate intermediate value theorem”.
As an immediate consequence we show that if 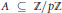 $A\subseteq \mathbb{Z}/p\mathbb{Z}$ is a set of cardinality
$A\subseteq \mathbb{Z}/p\mathbb{Z}$ is a set of cardinality 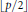 $\left\lfloor {p}/{2}\; \right\rfloor $ , then
$\left\lfloor {p}/{2}\; \right\rfloor $ , then 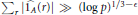 ${{\sum }_{r}}\widehat{|\,{{1}_{A}}}\left( r \right)|\gg {{\left( \log p \right)}^{1/3-\in }}$ . This gives a result on a “
${{\sum }_{r}}\widehat{|\,{{1}_{A}}}\left( r \right)|\gg {{\left( \log p \right)}^{1/3-\in }}$ . This gives a result on a “ 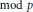 $\,\bmod \,p$ ” analogue of Littlewood's well-known problem concerning the smallest possible
$\,\bmod \,p$ ” analogue of Littlewood's well-known problem concerning the smallest possible 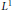 ${{L}^{1}}$ -norm of the Fourier transform of a set of
${{L}^{1}}$ -norm of the Fourier transform of a set of  $n$ integers.
$n$ integers.
Another application is to answer a question of Gowers. If 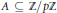 $A\,\subseteq \,{\mathbb{Z}}/{p\mathbb{Z}}\;$ is a set of size
$A\,\subseteq \,{\mathbb{Z}}/{p\mathbb{Z}}\;$ is a set of size 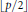 $\left\lfloor {p}/{2}\; \right\rfloor $ , then there is some
$\left\lfloor {p}/{2}\; \right\rfloor $ , then there is some 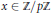 $x\,\in \,\mathbb{Z}/p\mathbb{Z}$ such that
$x\,\in \,\mathbb{Z}/p\mathbb{Z}$ such that
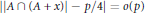 $$||A\cap \left( A+x \right)\,-\,p/4|\,=o\left( p \right).$$
$$||A\cap \left( A+x \right)\,-\,p/4|\,=o\left( p \right).$$
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2009
References
- 5
- Cited by

