Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-01-11T17:44:37.861Z Has data issue: false hasContentIssue false
  • English
  • Français

Existence de Solutions au Sens de Carathéodory Pour le Problème de Neumann y″ = f(t, y, y′)

Published online by Cambridge University Press:  20 November 2018

Zine E. A. Guennoun
Zine E. A. Guennoun*
Affiliation:
Département de mathématiques, physique et informatique, Université de Moncton, Moncton, N.-B. E1A 3E9
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We announce some existence results and their consequences for the Neumann problem of the nonlinear differential equation: 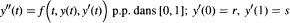where f: [0, 1] x ℝ2 → ℝ is a Carathéodory function and can grow very rapidly in the y′ variable.

Résumé

Résumé

Nous annonçons ici des résultats d'existence et leurs conséquences d'un problème de Neumann pour l'équation différentielle non linéaire: où ƒ: [0, 1] × ℝ2 → ℝ est une fonction de Carathéordory sous des conditions de croissance de non linéarité très rapide suivant la variable y′.

Keywords

34B1034B15
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 43 , Issue 5 , 01 October 1991 , pp. 998 - 1009
Copyright
Copyright © Canadian Mathematical Society 1991

References

Références

1. Bernstein, S., Sur les équations du calcul des variations, Ann. Sci. Ecole Norm. Sup. 29 (1912), 431–485.Google Scholar
2. Dugundji, J., Granas, A., Fixed point theory, vol. I, RW.N. Warszawa, 1982.Google Scholar
3. Granas, A., Sur la méthode de continuité de Poincaré, C.R. Acad. Sci. Paris 282 (1976), 983–985.Google Scholar
4. Granas, A., Guennoun, Z.E.A., Quelques résultats dans la théorie de Berstein-Carathéodory de l'équation y” = ƒ(t,y,y’), C.R. Acad. Sci. Paris 306 série 1 (1988), 703–706.Google Scholar
5. Granas, A., Guenther, R. B., Lee, J.W., On a theorem of S. Berstein, Pacific J. Math. 74 (1978), 67–82.Google Scholar
6. Granas, A., Nonlinear boundary value problems for some classes of ordinary differential equations, Rocky Mountain J. Math. 10 (1980), 35–58.Google Scholar
7. Granas, A., Nonlinear boundary value problems for ordinary differential equations. Dissertations Mathematics, CCSLIV, Warszawa, 1985.Google Scholar
8. Granas, A., Topological transversality II: Application to the Neumann problem for y” — f﹛t,y,y’), Pacific J. Math. 104 (1983), 95–109.Google Scholar
9. Guennoun, Z. E. A., Existence de solutions au sens de Carathéodory pour des problèmes aux limites non linéaires. Thèse de doctorat, Université de Montréal, 1989.Google Scholar
10. Mawhin, J., Points fixes, points critiques et problèmes aux limites. Les Presses de l'Université de Montréal 92,1985.Google Scholar
11. Nirenberg, L., Functional analysis. New York University Lecture Note Series, 1960.Google Scholar