Published online by Cambridge University Press: 20 November 2018
We consider a semilinear elliptic problem 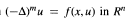 , (n > 2m). Under suitable conditions on f, we show the existence of a decaying positive solution. We do not employ radial arguments. Our main tools are weighted spaces, various applications of the Mountain Pass Theorem and LP regularity estimates of Agmon. We answer an open question of Kusano, Naito and Swanson [Canad. J. Math. 40(1988), 1281-1300] in the superlinear case:
, (n > 2m). Under suitable conditions on f, we show the existence of a decaying positive solution. We do not employ radial arguments. Our main tools are weighted spaces, various applications of the Mountain Pass Theorem and LP regularity estimates of Agmon. We answer an open question of Kusano, Naito and Swanson [Canad. J. Math. 40(1988), 1281-1300] in the superlinear case: 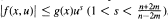 , and improve the results of Dalmasso [C. R. Acad. Sci. Paris 308(1989), 411-414] for the case
, and improve the results of Dalmasso [C. R. Acad. Sci. Paris 308(1989), 411-414] for the case 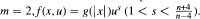 .
.