Published online by Cambridge University Press: 20 November 2018
Let 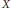 $X$ be a smooth projective geometrically connected curve over a finite field with function field
$X$ be a smooth projective geometrically connected curve over a finite field with function field 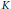 $K$. Let
$K$. Let 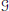 $g$ be a connected semisimple group scheme over
$g$ be a connected semisimple group scheme over 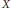 $X$. Under certain hypotheses we prove the equality of two numbers associated with
$X$. Under certain hypotheses we prove the equality of two numbers associated with 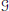 $g$. The first is an arithmetic invariant, its Tamagawa number. The second is a geometric invariant, the number of connected components of the moduli stack of
$g$. The first is an arithmetic invariant, its Tamagawa number. The second is a geometric invariant, the number of connected components of the moduli stack of 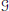 $g$-torsors on
$g$-torsors on 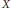 $X$. Our results are most useful for studying connected components as much is known about Tamagawa numbers.
$X$. Our results are most useful for studying connected components as much is known about Tamagawa numbers.