Published online by Cambridge University Press: 17 April 2009
Let M (N) be a σ–algebra of subsets of a set S (T) and let X, Y be Banach spaces with (,) a continuous bilinear map from X × Y into the scalar field. If μ: M → X (v: N → Y) is a vector measure and λ is the scalar measure defined on the measurable rectangles A × B, A ∈ M, B ∈ N, by λ(A×B) = 〈μ(A), v(B)〉, it is known that λ is generally not countably additive on the algebra generated by the measurable rectangles and therefore has no countably additive extension to the σ-algebra generated by the measurable rectangles. If μ (v) is an indefinite Pettis integral 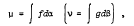 it is shown that a necessary and sufficient condition that λ have a countable additive extension to the σ-algebra generated by the measurable rectangles is that the function F: (s, t) → 〈f(s), g(t)〉 is integrable with respect to α × β.
it is shown that a necessary and sufficient condition that λ have a countable additive extension to the σ-algebra generated by the measurable rectangles is that the function F: (s, t) → 〈f(s), g(t)〉 is integrable with respect to α × β.