Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Malik, Sarfraz Nawaz
Mahmood, Shahid
Raza, Mohsan
Farman, Sumbal
and
Zainab, Saira
2018.
Coefficient Inequalities of Functions Associated with Petal Type Domains.
Mathematics,
Vol. 6,
Issue. 12,
p.
298.
Ravindar, B.
Sharma, R. B.
and
Magesh, N.
2019.
On a subclass of harmonic univalent functions defined by Ruscheweyh q-differential operator.
Vol. 2112,
Issue. ,
p.
020018.
Ravindar, B
and
BharaviSharma, R
2020.
Estimation Of Coefficients For A Novel Subclasses Of Harmonic Mappings.
IOP Conference Series: Materials Science and Engineering,
Vol. 981,
Issue. 2,
p.
022088.
Islam, Saeed
Khan, Muhammad Ghaffar
Ahmad, Bakhtiar
Arif, Muhammad
and
Chinram, Ronnason
2020.
Q-Extension of Starlike Functions Subordinated with a Trigonometric Sine Function.
Mathematics,
Vol. 8,
Issue. 10,
p.
1676.
Ahuja, Om
Anand, Swati
and
Jain, Naveen Kumar
2020.
Bohr Radius Problems for Some Classes of Analytic Functions Using Quantum Calculus Approach.
Mathematics,
Vol. 8,
Issue. 4,
p.
623.
Chen, Xiao-Diao
Yu, Junle
Ma, Junyi
and
Jiang, Nichang
2021.
New Approximation Formulas for Tighter Bounds of the Q-Function and its Applications.
Wireless Personal Communications,
Vol. 121,
Issue. 3,
p.
2111.
Long, Pinhong
Liu, Jinlin
Gangadharan, Murugusundaramoorthy
and
Wang, Wenshuai
2022.
Certain subclass of analytic functions based on $ q $-derivative operator associated with the generalized Pascal snail and its applications.
AIMS Mathematics,
Vol. 7,
Issue. 7,
p.
13423.
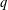 $q$-FUNCTION THEORY
$q$-FUNCTION THEORY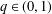 $q\in (0,1)$, we obtain the Herglotz representation theorem and discuss the Bieberbach problem for the class of
$q\in (0,1)$, we obtain the Herglotz representation theorem and discuss the Bieberbach problem for the class of 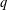 $q$-convex functions of order
$q$-convex functions of order  $\unicode[STIX]{x1D6FC}$ with
$\unicode[STIX]{x1D6FC}$ with 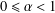 $0\leq \unicode[STIX]{x1D6FC}<1$. In addition, we consider the Fekete–Szegö problem and the Hankel determinant problem for the class of
$0\leq \unicode[STIX]{x1D6FC}<1$. In addition, we consider the Fekete–Szegö problem and the Hankel determinant problem for the class of 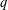 $q$-starlike functions, leading to two conjectures for the class of
$q$-starlike functions, leading to two conjectures for the class of 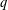 $q$-starlike functions of order
$q$-starlike functions of order  $\unicode[STIX]{x1D6FC}$ with
$\unicode[STIX]{x1D6FC}$ with 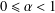 $0\leq \unicode[STIX]{x1D6FC}<1$.
$0\leq \unicode[STIX]{x1D6FC}<1$.