Published online by Cambridge University Press: 10 July 2019
Let 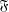 $\mathfrak{F}$ be a class of finite groups and
$\mathfrak{F}$ be a class of finite groups and 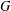 $G$ a finite group. Let
$G$ a finite group. Let 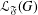 ${\mathcal{L}}_{\mathfrak{F}}(G)$ be the set of all subgroups
${\mathcal{L}}_{\mathfrak{F}}(G)$ be the set of all subgroups 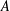 $A$ of
$A$ of 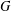 $G$ with
$G$ with 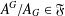 $A^{G}/A_{G}\in \mathfrak{F}$. A chief factor
$A^{G}/A_{G}\in \mathfrak{F}$. A chief factor 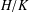 $H/K$ of
$H/K$ of 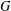 $G$ is
$G$ is 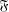 $\mathfrak{F}$-central in
$\mathfrak{F}$-central in 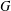 $G$ if
$G$ if 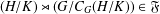 $(H/K)\rtimes (G/C_{G}(H/K))\in \mathfrak{F}$. We study the structure of
$(H/K)\rtimes (G/C_{G}(H/K))\in \mathfrak{F}$. We study the structure of 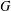 $G$ under the hypothesis that every chief factor of
$G$ under the hypothesis that every chief factor of 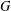 $G$ between
$G$ between 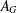 $A_{G}$ and
$A_{G}$ and 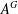 $A^{G}$ is
$A^{G}$ is 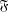 $\mathfrak{F}$-central in
$\mathfrak{F}$-central in 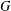 $G$ for every subgroup
$G$ for every subgroup 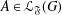 $A\in {\mathcal{L}}_{\mathfrak{F}}(G)$. As an application, we prove that a finite soluble group
$A\in {\mathcal{L}}_{\mathfrak{F}}(G)$. As an application, we prove that a finite soluble group 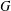 $G$ is a PST-group if and only if
$G$ is a PST-group if and only if 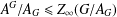 $A^{G}/A_{G}\leq Z_{\infty }(G/A_{G})$ for every subgroup
$A^{G}/A_{G}\leq Z_{\infty }(G/A_{G})$ for every subgroup 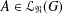 $A\in {\mathcal{L}}_{\mathfrak{N}}(G)$, where
$A\in {\mathcal{L}}_{\mathfrak{N}}(G)$, where 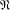 $\mathfrak{N}$ is the class of all nilpotent groups.
$\mathfrak{N}$ is the class of all nilpotent groups.
Research of the first author is supported by the China Scholarship Council and NNSF of China (11771409).