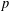 $p$-GROUPS ALL OF WHOSE NONNORMAL SUBGROUPS HAVE BOUNDED NORMAL CORES
$p$-GROUPS ALL OF WHOSE NONNORMAL SUBGROUPS HAVE BOUNDED NORMAL CORESPublished online by Cambridge University Press: 18 July 2019
Given a positive integer  $m$, a finite
$m$, a finite 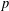 $p$-group
$p$-group 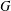 $G$ is called a
$G$ is called a 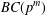 $BC(p^{m})$-group if
$BC(p^{m})$-group if 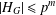 $|H_{G}|\leq p^{m}$ for every nonnormal subgroup
$|H_{G}|\leq p^{m}$ for every nonnormal subgroup 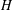 $H$ of
$H$ of 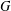 $G$, where
$G$, where 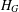 $H_{G}$ is the normal core of
$H_{G}$ is the normal core of 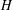 $H$ in
$H$ in 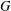 $G$. We show that
$G$. We show that 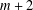 $m+2$ is an upper bound for the nilpotent class of a finite
$m+2$ is an upper bound for the nilpotent class of a finite 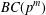 $BC(p^{m})$-group and obtain a necessary and sufficient condition for a
$BC(p^{m})$-group and obtain a necessary and sufficient condition for a 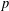 $p$-group to be of maximal class. We also classify the
$p$-group to be of maximal class. We also classify the 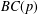 $BC(p)$-groups.
$BC(p)$-groups.
This work was supported by the National Natural Science Foundation of China (11671324, 11471266).