China is currently facing challenges of both overweight and underweight. Obesity and overweight are major risk factors for developing non-communicable chronic diseases, including type 2 diabetes, CVD, hypertension and stroke, and certain forms of cancer(1, Reference He, Jiang and Yang2). This burgeoning public health concern has prompted numerous interventions to facilitate healthy weight management. However, to design an appropriate weight loss intervention for this population, it is essential to accurately assess their energy requirement. This assessment is best accomplished by measuring the basal energy expenditure (BEE) of each subject. BEE can be measured using devices such as direct and indirect calorimeters and respiratory chambers, but the operation of these devices requires trained personnel and it is expensive and time consuming. For these reasons, calculation of BEE by mathematical equations has been adopted as a major method of assessing the energy requirement of individuals(Reference Frankenfield, Roth-Yousey and Compher3).
However, there exist several published empirical equations for estimating BEE from anthropometrical variables, including body weight, height, age and sex of healthy adult subjects. In practice, these equations are routinely used to estimate energy requirements. For instance, Chinese recommended nutrient intakes of energy are derived from the FAO/WHO/UNU equations to predict BEE. However, FAO/WHO/UNU equations were developed using the Schofield database that contained a disproportionate number – 3388 out of 7173 (47 %) – of Italian subjects. The Schofield database contained relatively few subjects from the tropical regions(4, Reference Henry5). BEE studies conducted more recently have shown that the predicted values using the FAO/WHO/UNU equations overestimated BEE in Asian and Chinese subjects(Reference Case, Brahler and Heiss6, Reference Leung, Woo and Chan7).
With the emergence of new advanced technology in recent years, measurements of BEE have become easier and more reproducible, providing a good opportunity to re-examine BEE and estimating total energy requirements. Although there is now a considerable body of BEE data from individuals living in Western countries, there are still relatively few data on individuals living in other parts of the world. Moreover, there is a glaring lack of BEE data from mainland China(Reference Henry5). Hence, the purpose of the present study was to measure BEE of southern Chinese healthy adults and to develop a new equation for predicting BEE in southern Chinese healthy adults.
Materials and methods
Subjects
A total of 165 recruited healthy Chinese adults aged 18–45 years with normal body weight (BMI, 18·5–24·0 kg/m2) were involved in the present study. All the subjects were from the southern areas of the Yangtze River (China) and had been living in Chengdu for at least 2 years. They were recruited through notice-board postings and at university lectures for students. Subjects with thyroid diseases, insulin-dependent diabetes mellitus, renal diseases, chronic obstructive pulmonary disease, under medication, history of recent weight loss, unusual dietary practices and women with irregular menstrual cycles, or who were pregnant or lactating were excluded. The data of eight subjects were excluded because these data were invalid: six of them disobeyed the procedure in he pretest, one had a device leakage(Reference McClave and Snider8) and the other was falling asleep during measurement. Finally, the data of 165 subjects (79 males and 86 females) remained in the analysis.
The present study was conducted according to the guidelines laid down in the Declaration of Helsinki, and all procedures involving human subjects were approved by the National Institute for Nutrition and Food Safety Chinese Center for Disease Control and Prevention ethical review committee. Written informed consent was obtained from all subjects. The subjects were financially compensated for participating in the present study.
The determination of basal energy expenditure
BEE was measured from pulmonary gas exchange using a breath-by-breath portable gas analyser (Cosmed K4b2, Rome, Italy). Subjects were instructed to refrain from eating for at least 12–14 h after a meal low in fat and dietary fibre and to avoid smoking, drinking and doing vigorous exercises during the measurement period. Moreover, female subjects were instructed to schedule their appointments to avoid the menstrual period because of the requirement for 24 h urinary nitrogen analysis, which was involved in BEE calculation.
Subjects had been asked to stay in a hotel and become accustomed to the apparatus, face mask and the surrounding environment on the day before the experiment day. All calorimetric measurements were performed by one investigator according to standardised protocols. BEE measurements were performed in the morning for at least 6 min at a thermoneutral room with a temperature of 24·97 ± 2·05°C and a relative humidity of 64·79 ± 8·96 %. The subjects were awakened from sleep, kept fully awake and lied down quietly and completely relaxed during the measurements. BEE was repeatedly measured in the same individual on consecutive 2 d, and steady-state data in the 2 d were averaged and were used for the analysis of BEE. Steady-state data here meant a total of 12 min of data in the 2 d with a breath-by-breath record on O2 consumption and CO2 production in which values were within mean and 2 sd.
The Cosmed K4b2 contains a portable unit (a part of the Cosmed K4b2 that contains O2 and CO2 analysers) and three face masks with different sizes. The flexible face mask, covering a subject's mouth and nose, was attached to a flow meter. The flow meter is a bidirectional digital turbine. The face mask was secured to the subjects with a nylon mesh hairnet and Velcro straps. A disposable gel seal was placed between the face mask and the subject's face to provide an airtight seal. Before each test, the Cosmed K4b2 system was warmed up for at least 45 min, with O2 and CO2 analysers calibrated using ambient air and reference gas with 16 % O2 and 5 % CO2. The flow meter was calibrated by a 3 litre syringe (Quinton Instruments, Seattle, WA, USA).
On the day that BEE was measured, urine was collected over a 24 h period to measure daily urinary nitrogen (g/d). Total urinary nitrogen was determined by a standard Kjeldahl method(9). BEE was calculated using O2 consumption, CO2 production and urinary nitrogen production with the Weir equation(Reference Weir10):
Here, VO2 represents O2 consumption in l/d; VCO2 represents CO2 production in l/d; UN represents 24 h urinary nitrogen production in g/d.
Comparison between the measured basal energy expenditure and the predicted values using predictive equations in the literature
The predictive equations of Harris–Benedict (HB)(Reference Roza and Shizgal11), Schofield et al. (Reference Schofield, Schofield and James12), Liu et al. (Reference Liu, Lu and Chen13) and Henry(Reference Henry5) were used for calculating BEE. These equations were chosen because they had been widely used in healthy Chinese population studies (equations of HB and Schofield), derived based on a Chinese database (Liu equation), or reported to be better suitable for a Chinese population (Henry equation)(Reference Li and Qu14).
Measurement of body composition and body surface area
Standing height ( ± 1 mm) and weight ( ± 0·01 kg, A&D, HW100KGL, Japan) were measured after the measurement of BEE. Fat-free mass (FFM) was assessed by means of bioelectrical impedance analysis; resistance and reactance were measured while the subjects were in the supine position using an ImpediMed body composition analyser according to the manufacturer's instructions (Impedimed IMP DF50, QLD, Australia; 50 kHz). The value for FFM was calculated using the following equations(Reference Houtkooper, Lohman and Going15):
where Z is the bioelectrical impedance in Ω; R is the resistance in Ω; C is the reactance in Ω; FFM is measured in kg; H is the height in cm; W is the weight in kg; A is the age in year; S is the sex (male = 1 and female = 0).
Body surface area (BSA) was calculated using the following formula proposed by Zhao et al. (Reference Zhao, Liu and Yao16). For men, BSA (m2) = 0·00 607 height (cm)+0·0127 weight (kg) − 0·0698 l. For women, BSA (m2) = 0·00 586 height (cm)+0·0126 weight (kg) − 0·0461(Reference Zhao, Liu and Yao17).
Data analysis
Statistical analysis was performed using the SPSS software package for MS Windows (release 15.0; SPSS, Inc., Chicago, IL, USA) and Microsoft Excel 2003. Statistical significance was set at P < 0·05 (two-sided test). The relationship between BEE measured by indirect calorimetry and the predictive variables was assessed using Pearson's correlation. Independent variables were FFM, BSA, body weight, height, sex and age. Multiple regressions were used to derive a new prediction equation to estimate BEE. The coefficient of correlation (r), the coefficient of determination (r 2), sem and the residual standard deviation (RD) were generated in the linear regression analyses as measures of goodness of fit of the newly developed equations. The relationship between BEE measured by Cosmed K4b2 and the corresponding BEE calculated from predictive equations was assessed using Student's paired t test (statistical difference between means).
Results
Anthropometric characteristics and measured basal energy expenditure of subjects
Males were taller and heavier, and had greater FFM and greater BSA than females (P = 0·001). However, no significantly statistical differences were detected for age (P = 0·78) and BMI (P = 0·37) between the male and the female subjects. Results revealed that the males had a higher BEE, consumed more O2 and produced more CO2 than females (P = 0·001) (Tables 1 and 2).
Table 1 Anthropometric characteristics of subjects
(Mean values with their standard errors and ranges)
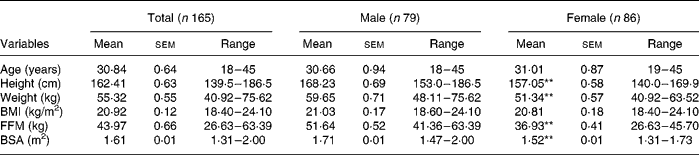
FFM, fat-free mass by bioelectrical impedance analysis; BSA, body surface area.
Mean values were significantly different from those for the males: **P = 0·001 (two-sided).
Table 2 Measured basal energy expenditure data of subjects
(Mean values with their standard errors)
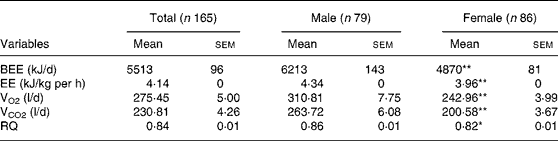
BEE, basal energy expenditure; EE, energy expenditure; VCO2, CO2 production per day.
Mean values were significantly different from those for the males: *P = 0·05, **P = 0·001 (two-sided).
Correlation between the measured basal energy expenditure and predictive variables
According to Pearson correlation analysis, the measured BEE (mBEE) correlated best with BSA (r 0·70) and FFM (r 0·69). Both BSA and FFM correlated well with weight, height and sex (r 0·97, 0·92 and 0·84; r 0·91, 0·69 and 0·87, respectively, P = 0·01) (Table 3). When BEE was adjusted for weight, BSA and FFM, the males had a higher BEE adjusted for weight and BSA (104 kJ/kg weight, 3626 kJ/m2 BSA) than the females (95 kJ/kg weight, 3197 kJ/m2 BSA, P = 0·001). Whereas females had a higher BEE adjusted for FFM (132 kJ/kg FFM) than males (120 kJ/kg FFM, P = 0·001).
Table 3 Pearson correlation coefficient for basal energy expenditure (BEE, kJ/d) and other predictive variables
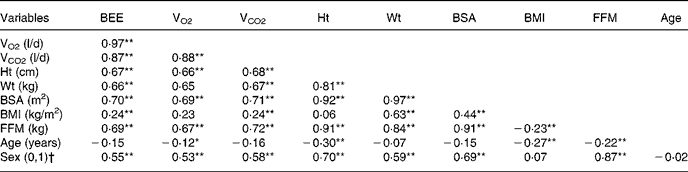
VCO2, CO2 production per day; BSA, body surface area; FFM, fat-free mass by bioelectrical impedance analysis.
* Correlation is significant at the 0·05 level (two-sided).
** Correlation is significant at the 0·01 level (two-sided).
† Female = 0 and male = 1.
Development of a new equation with Cosmed K4b2 for predicting basal energy expenditure in southern Chinese healthy adults
The correlation between mBEE and predictive variables is presented in Table 3. Strong relationships were found between BEE and BSA, FFM, weight, height and sex. These parameters were therefore used for deriving the equation for estimation of BEE in southern Chinese healthy adults.
Multiple regression analysis was used for deriving formulae predicting BEE (Table 4). When only one variable was considered, BSA yielded the highest r 2 and the lowest RD (r 2 0·50, RD = 874). When FFM, height and weight were used for multiple regression analysis, r 2 0·47, 0·45 and 0·44, RD = 897, 911 and 923, respectively. Derivative equations contained variables in the following combinations: weight with height, height with sex yielded almost the same greatest accuracy (r 2 0·49 and 0·46; RD = 877 and 901, respectively), weight with height combination yielded better accuracy, but all indicated that height and weight had a significant collinearity relationship (for height, Eigenvalue = 0 for the combinations of weight and height, condition index = 74·64, Pearson correlation coefficient between height and weight r 0·81, P = 0·001)(Reference Zhang18). Adding height to the analysis did not increase accuracy significantly. On the contrary, it led to the presence of collinearity in the equations, and we also can see that the equation which contains height had the greatest negative constant. According to professional knowledge, we excluded height from the predictive equations, and developed the equation with the most goodness of fit that contained variables in the following combinations: weight and sex in equation number 7 (equation 7, r 2 0·48, RD = 890, Table 4).
Table 4 Generalised regression equations for predicting basal energy expenditure (kJ/d) in southern Chinese healthy adults
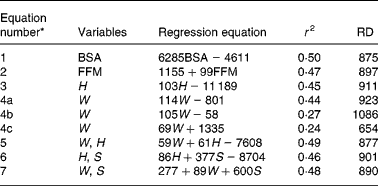
RD, residual standard deviation; BSA, body surface area (m2); FFM, fat-free mass (kg); W, weight (kg); H, height (cm); S, sex (female = 0 and male = 1); r 2, the coefficient of determination.
* Equation numbers 1–3, 4a and 5–7 are derived from the data of total subjects (n 165); equation no. 4b is derived from the data of male subjects (n 79); equation no. 4c is derived from the data of female subjects (n 86).
Considering the existing significantly statistical difference of the BEE values between the males and the females, we also derived predictive equations based on the male and female data separately, as shown in Table 4. However, the sex-specific equations had a lower r 2 value (for males, r 2 0·27; for females, r 2 0·24, Table 4).
Comparison between measured basal energy expenditure and predicted values using predictive equations
Paired t tests were used to compare the differences between mBEE in the present study and predicted BEE (pBEE) using predictive equations developed by Liu (eq-Liu), Henry, Schofield and HB (Table 5). The mBEE in the present study significantly correlated with the BEE values obtained with the eq-Liu (r 0·71). No significant differences were observed between the mBEE 5513 (sem 96) kJ/d and the predicted values estimated using the eq-Liu 5579 (sem 57) kJ/d (P = 0·34, Table 6). In contrast, the BEE estimated by the equations developed by Henry 5763 (sem 54) kJ/d, equations developed by Schofield 5898 (sem 58) kJ/d and equations developed by HB 5863 (sem 51) kJ/d was significantly higher than the mBEE (P = 0·001 for all).
Table 5 Predictive equations for estimation of basal energy expenditure based on the equation derived by other authors

W, weight (kg); H, height (cm); A, age (years), S, sex, HB, Harris–Benedict.
Table 6 Mean difference and correlation coefficient between measured basal energy expenditure (mBEE, kJ/d) in the present study and predicted BEE using predicted equations (pBEE, kJ/d) for subjects aged 18–45 years
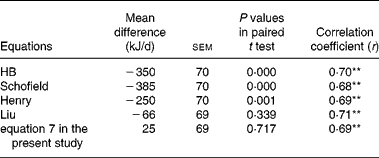
HB, Harris–Benedict.
Mean difference (kJ/d) = mBEE (kJ/d) − pBEE (kJ/d).
** Correlation is significant at the 0·01 level (two-sided).
The results of the paired t test between mBEE in the present study and pBEE indicated that the best pBEE was the results from eq-Liu, so the validity and exactness of new equation 7 developed by the present study were compared with predictive eq-Liu. Linear regression analysis showed that there was a strong correlation between mBEE and pBEE estimated from the eq-Liu (pBEE-eqLiu) and equation 7 (pBEE-equation 7) (Figs. 1 and 2):
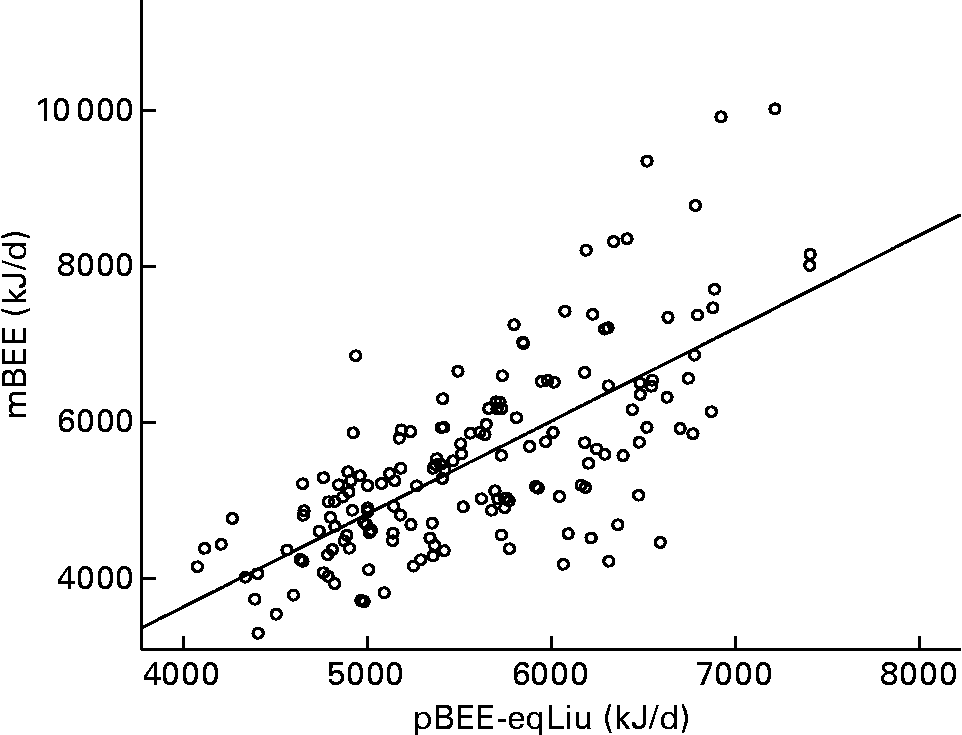
Fig. 1 Linear regression between mBEE (measured basal energy expenditure with Cosmed K4b2) and pBEE-eqLiu (basal energy expenditure calculated with the predictive equation developed by Liu; r 0·71, P < 0·001).

Fig. 2 Linear regression between mBEE (measured basal energy expenditure with Cosmed K4b2) and pBEE-equation 7 (basal energy expenditure calculated with the predictive equation number 7 developed in the present study; r 0·69, P < 0·001).
High concordance between values estimated from the eq-Liu (pBEE-eqLiu) and equation 7 (pBEE-equation 7) was also evident on application of the linear regression (Fig. 3):

Fig. 3 Linear regression between pBEE-Liu and pBEE-equation 7. pBEE-eqLiu, basal energy expenditure calculated with predictive equation developed by Liu; pBEE-equation 7, basal energy expenditure calculated with the equation number 7 developed in the present study; r 0·97, P < 0·001.
Discussion
So far, most studies for a practical and valid method to assess BEE have been focused on Western countries. To the best of our knowledge, there is only one BEE study on Chinese adults, and there is no information on BEE from mainland China, the most populated region in the world(Reference Henry5).
BMR is defined as the amount of energy used for maintaining basal metabolism in a period of time and is measured under standard conditions that include being awake in the supine position after 10–12 h of fasting and 8 h of physical rest, and being in a state of mental relaxation in an ambient environmental temperature that does not elicit heat-generating or heat-dissipating processes(Reference Cuerda, Ruiz and Velasco19). These requirements (i.e. the absence of gross muscular activity, a post-absorptive state, thermoneutral environment, etc.) were strictly met in the present study in order to ensure basal levels of metabolism, so that measurements made between individuals or in the same individual over time are comparable and that biological significance can be imparted to differences that are observed under these conditions(Reference Shetty20).
The data from eight subjects were excluded from further analysis because no valid BEE measurements were obtained during indirect calorimetric measurements due to a device leakage (n 1)(Reference McClave and Snider8), violation of the pre-test conditions (n 6) or sleeping during measurement (n 1). Smoking or drinking within 12 h before the BEE measurement would lead to overestimation of BEE, because leakage or sleeping during measurement could result in an underestimation of BEE(Reference Solomon, Kurzer and Calloway21).
The present results demonstrate that there is a good agreement between the mBEE and the pBEE using the eq-Liu, because the eq-Liu was derived from a Chinese database and studies that were conducted more recently. Moreover, both the present study and Liu's used open-circuit indirect calorimetry (Cosmed K4b2v. metabolic measurement cart), and we believe that these are crucial because there have been studies that demonstrated that closed-circuit indirect calorimetry is more likely to lead to higher BMR values compared with opened-circuit indirect calorimetry ( ± 5·6 %)(Reference Henry5, Reference Shetty20, Reference Clark and Hoffer22). The human body is in dynamic state; lifestyle, body composition and foods ingested change with time.
Although the Henry equation was reported to better predict BEE in Chinese(Reference Li and Qu14), we found that the Henry equation significantly overestimated the Chinese BEE (P = 0·001). A possible reason for the overestimation error in the prediction of RMR for Chinese with equations such as the Schofield equation that have been widely used in the clinical nutrition field may be largely explained by the fact that the Schofield equation was developed using the Schofield database that comprised a disproportionate number (3388 out of 7173 (47 %)) of Italian subjects. Italian subjects had a higher BMR/kg than any other group in the Schofield database. Since the Schofield database contains relatively few subjects from the tropical regions (322 Indian and 615 tropical residents), and the Schofield equations were developed using measurements made over eight decades ago, it is not surprising that the equations fail to accurately calculate BEE in populations in other parts of the world, including Chinese(Reference Henry5, Reference Soares, Francis and Shetty23).
The HB equation has been widely used for estimating BMR. The multiple regression equation was developed in 1919 for predicting an individual's BEE. The present findings indicate that the HB equation overestimated BEE by an average of 385 (sem 70) kJ/d. The differences may be accounted for by modernisation of equipment used in the present study. Subject differences, climatic factors, the levels of physical activity and foods ingested have all changed over the eight decades since completion of the HB study(Reference Daly, Heymsfield and Head24). The early workers also noted a training factor, with repeated measurements of energy expenditure on the same subject decreasing by 8–10 % from the initial measurement, whereas in the present study, each individual BEE was repeatedly measured on consecutive 2 d to minimise the intra-individual variance. Similar differences have been found in other studies(Reference Henry5, Reference Daly, Heymsfield and Head24, Reference Skouroliakou, Giannopoulou and Kostara25). Hence, the present findings suggest that these three commonly used BEE predictive equations (Henry, HB and Schofield) developed on the basis of the Western population database are not appropriate for the Chinese population.
Some study limitations need to be addressed. Because we also measured total energy expenditure using a double-labelled water method on some urban subjects whose urine was collected daily, the subjects continuously ate a ‘standard diet’ for 16 d during the trial (the results will be reported in another paper). Both studies included subjects from various occupations; therefore, good compliance could hardly be achieved simultaneously. Most urban subjects in the present study were college students who were younger (24·4 years) and had a relatively lower BMI (20·60 kg/m2, in the normal body weight range) than other studies(Reference Liu, Lu and Chen13). However, previous practice in assessing energy requirements had indicated that body weight varied in composition, and hence in energy requirement. In addition, adjustment procedures using ratio scaling, i.e. per kg body weight, often overestimated the energy transduction of individuals with small body weight and underestimated that of individuals with large body weight(Reference Norgen26). And still some studies reported that the coefficient of inter-individual variability depended upon the variations in body size; the larger the variation in body weight among subjects, the larger the CV of total energy expenditure(Reference Garby, Lammert and Nielsen27). Further studies in the measurement of Chinese BEE may be necessary to involve more various occupations.
Conclusions
mBEE of southern Chinese healthy adults was 5513 (sem 96) kJ/d. The BMR of Chinese adults of normal weight is overestimated by widely used prediction equations developed by Henry, Schofield and HB. The equation developed in the present study (equation 7) can be used in predicting BEE for Chinese adults aged 18–45 years with normal body weight.
Acknowledgements
None of the authors has a known conflict of interest. The present study was supported by a project of Ministry of Science and Technology, People's Republic of China (2008BAI58B01). Xg. Y., J. P., Q. Z. and D. M. provided technical support. J. P., C. H. and Xj. Y. designed the study. Xj. Y., M. L., C. H. and G. Z. carried out the recruitment of the subjects. Xj. Y., D. M. and M. L. completed BEE determination. Xj. Y., M. L. and Q. Z. analysed urinary nitrogen. W. H. provided diet for subjects, and Xj. Y. and C. H. performed the data analyses. Xj. Y., C. H., Q. Z. and D. M. wrote, edited and reviewed the final manuscript.











