Article contents
A Teacher's Remark on Exact Credibility
Published online by Cambridge University Press: 29 August 2014
Extract
In the classical Bayesian approach to credibility the claims are conditionally independent and identically distributed random variables, with common density f(x, ϑ). The unknown parameter ϑ is a realization of a random variable Θ having initial (prior) density u(ϑ). Let
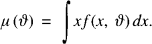
The initial pure premium is
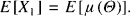
The premium for X t + 1, given X1 +, …, Xt, is the conditional expectation
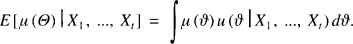
A central question is for which pairs f(x, ϑ) and u (ϑ) this expression is linear, i.e. of the form
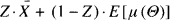
where 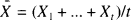 is the observed average. This is indeed the case for about half a dozen famous examples. Jewell (1974) has found an elegant and general approach to unify these examples, see also Goovaerts and Hoogstad (1987, chapter 2). The classical examples can be retrieved as special cases; however a preliminary reparameterization has to be performed on a case by case basis. The purpose of this note is to propose an alternative (but of course strongly related) formulation of the general model, from which the classical examples can be retrieved in a straightforward way.
is the observed average. This is indeed the case for about half a dozen famous examples. Jewell (1974) has found an elegant and general approach to unify these examples, see also Goovaerts and Hoogstad (1987, chapter 2). The classical examples can be retrieved as special cases; however a preliminary reparameterization has to be performed on a case by case basis. The purpose of this note is to propose an alternative (but of course strongly related) formulation of the general model, from which the classical examples can be retrieved in a straightforward way.
Information
- Type
- Short Contribution
- Information
- Copyright
- Copyright © International Actuarial Association 1995
References
- 4
- Cited by

