I. INTRODUCTION
The aim of temporal frame interpolation (TFI) is to insert frames at the decoder that are not present at the encoder. TFI is used in a variety of video coding applications, for example to reduce ghosting artifacts and motion blur in liquid crystal displays [Reference Chan and Nguyen1], or in distributed video coding, where temporally interpolated frames are used as side information for the Wyner–Zyv decoding [Reference Girod, Aaron, Rane and Rebollo-Monedero2]. In scalable video coding, where video can be decoded at different quality levels in terms of spatial, bit-rate, and temporal resolution, TFI is desirable when all information at a certain temporal level is quantized to zero.
In current state-of-the-art codecs, motion fields are coded using blocks; each pixel in the target frame is assigned a vector pointing to the location in the reference frame where the block it belongs to matches best according to some error measure. This block motion does not in general represent the “true” motion, but one which minimizes the prediction error. It is therefore ill-suited to represent motion in the vicinity of motion discontinuities, and cannot be scaled to represent motion to intermediate frames. For these reasons, good-performing TFI methods first (re-)estimate the motion between the two frames where a frame is to be inserted, which is then used to interpolate the target frame. Different frame interpolation (FI) methods have been proposed, which differ in terms of type of motion estimation (ME) performed, as well as where those motion fields are anchored. Also, various strategies and texture optimizations are applied to create the interpolated frame.
A large body of TFI algorithms use block motion fields, which have comparatively low computational complexity. In order to avoid blocking artifacts, various techniques which smooth the interpolated frames are employed. Choi et al. [Reference Choi, Han, Kim and Ko3] use bilateral ME, and block artifacts are reduced using an adaptive overlapped block motion compensation based on the reliability of neighboring motion vectors. Wang et al. [Reference Wang, Zhang, He and Tan4] perform motion-compensated prediction of the intermediate frame from both reference frames independently, and then blend these predictions together using a trilateral filter. Dikbas and Altunbasak [Reference Dikbas and Altunbasak5] use an adaptive interpolation between the forward and backward warped frames. Their method has low computational complexity, but the implicit occlusion handling can lead to severe visual distortions if disoccluded regions become large. Jeong et al. [Reference Jeong, Lee and Kim6] perform motion-compensated FI using a multi-hypothesis ME. The best motion hypothesis is selected by optimizing the cost function of a labeling problem. Pixels in the target frame are computed as a weighted combination of several pixels from the reference frame. They show improved reconstruction quality, at the expense of a significant increase in computational complexity. Veselov and Gilmutdinov [Reference Veselov and Gilmutdinov7] propose a hierarchical bidirectional multi-stage ME algorithm. They partition the target frame into non-overlapping, hierarchical blocks, and approximate the “true” motion flow. Each pixel is blended from multiple reference pixels. Zhang et al. [Reference Zhang, Xu, Ji and Dai8] propose a polynomial motion approximation model in order to account for intensity changes across frames. Their method can be applied to exiting TFI schemes and improve the quality of interpolated frames at the expense of increased memory and computational complexity.
To avoid artificial boundaries created by block motion fields, Chin and Tsai [Reference Chin and Tsai9] estimate a dense motion field, and apply the motion to each pixel location. Simple heuristics are used to handle holes and multiple mapped locations in the upsampled frame. Several FI methods have been proposed which try to detect occluded regions, and show improved performances compared with methods without occlusion handling. Kim et al. [Reference Kim, Lim and Park10] use linearity checking between the estimated forward and backward motion fields to detect occluded regions. Cho et al. [Reference Cho, Lee and Park11] use a bidirectional ME scheme that is based on feature trajectory tracking, which allows us to detect occluded regions.
In [Reference Rüfenacht, Mathew and Taubman12], we have shown how the bidirectional hierarchical anchoring (BIHA) framework naturally lends itself to TFI when all information at a certain temporal level is quantized to zero. The present paper represents an extension of this earlier conference paper. A key distinguishing feature of the proposed bidirectional, occlusion-aware temporal frame interpolation (BOA-TFI) framework is that the interpolation process is driven entirely by piecewise-smooth motion estimates that are anchored at reference frames and considered to represent physical motion. Motion estimated at reference frames is mapped to target frames where it is used to directly infer regions of occlusion and disocclusion. Motion discontinuities at reference frames are explicitly discovered and play a key role in the motion mapping process. We do not use block motion, as it is ultimately not reflective of the underlying physical reality. We also avoid the use of non-physical averaging processes such as overlapped block motion compensation (OBMC), as employed in most state-of-the-art schemes; such approaches can rarely be justified as modeling an underlying physical process, and often result in oversmooth interpolated frames.
This motion centric approach is well adapted to scalable compression schemes [Reference Rüfenacht, Mathew and Taubman13], because it allows the motion to be understood as part of a transform that is applied to the frame data; the proposed TFI scheme can then be understood as the inverse transform that would result if high temporal frequency details were omitted. We expect that this property will be valuable in enabling seemless integration of video decoding and interpolation processes in the future. In the interest of conciseness, however, this paper focuses only on the TFI problem, leaving the interesting connection with compression to other works.
The motion centric approach means that we do not use texture information (pixel values) as part of the detailed reasoning for the FI process. Frame texture information is used only to derive the piecewise-smooth motion representation itself. Recently, there have been various proposals from the computer vision community on how such motion fields can be estimated. Xu et al. [Reference Xu, Jia and Matsushita14] propose a motion detail preserving optical flow algorithm (MDP), which encourages sharp discontinuities in the motion field. Wulff and Black [Reference Wulff and Black15] propose a layered motion model, which is able to obtain piecewise-smooth motion fields with sharp discontinuities on sequences that are heavily affected by motion blur. While currently limited to two motion layers, this work shows a lot of promise.
With respect to its conference version [Reference Rüfenacht, Mathew and Taubman12], in this paper we report on improvements that have made the proposed scheme more robust; we also give a much more detailed description of the fundamental concepts of the proposed TFI scheme. Furthermore, we provide a more extensive experimental validation on a large variety of natural sequences, as well as very challenging computer-generated sequences, which turn out to be more difficult than most common natural test sequences. Compared with the prior art, the main differences of the proposed BOA-TFI scheme are:
-
• High-quality disocclusion masks are computed, which are used to guide the bidirectional prediction of the interpolated frame – we switch to appropriate unidirectional prediction in regions which are occluded in one reference frame.
-
• Estimated motion field discontinuity information allows us to reliably identify the foreground object in regions of motion field folding (i.e., resolve double mappings).
-
• If used with our highly scalable video coding (HSVC) scheme, motion fields which were estimated at the encoding stage can be (re)used for FI, which significantly reduces the computational complexity at the decoder. Additionally, motion fields can be estimated on high-quality texture data at the encoder, as opposed to decoded frames which might suffer from compression artifacts.
II. OVERVIEW
Figure 1 gives an overview of the proposed TFI method, where we used the notation introduced in Table 1. Inputs to the method are the reference frames f
a
and f
c
, and the (potentially estimatedFootnote
1
) motion field between them,
![]() $M_{a \rightarrow c}$
. The proposed scheme involves two types of operations on motion fields: motion inference and motion field inversion. Both these operations involve mapping a motion field from one frame to another, which likely leads to double mappings (because of folding of the motion field), as well as holes in regions that get disoccluded. Both double mappings and disoccluded regions are handled by reasoning about the displacement of motion discontinuities.
$M_{a \rightarrow c}$
. The proposed scheme involves two types of operations on motion fields: motion inference and motion field inversion. Both these operations involve mapping a motion field from one frame to another, which likely leads to double mappings (because of folding of the motion field), as well as holes in regions that get disoccluded. Both double mappings and disoccluded regions are handled by reasoning about the displacement of motion discontinuities.

Fig. 1. Overview of the proposed TFI method: The input to the scheme are a (potentially estimated) motion field M a→c , as well as breakpoint fields estimated on M a→c for frame f a , and on M c→e (only used to obtain breakpoints) for frame f c ; furthermore, the two reference frames f a and f c . In the first step, estimated breakpoints at reference frames f a and f c (B a and B c ) are transferred to the target frame f b (B b ). Next, M a→b is obtained by halving its parent motion field M a→c . M a→c and M a→b are then used to infer the motion field M c→b . The last step consists of inverting M a→b and M c→b to obtain M̂ b→a and M̂ b→c . During the motion inversion process, we compute disocclusion masks Ŝ b→a and Ŝ b→c , which are used to guide the bidirectional MCTFI process to temporally interpolate the frame f̂ b . Breakpoints are used to resolve double mappings and handle occluded regions during both the motion inference and inversion process.
Table 1. Table of notations used throughout the paper.

A variety of ways can be employed to represent motion discontinuities in the proposed framework. Because this work comes out of a highly scalable video coder [Reference Rüfenacht, Mathew and Taubman13], we use breakpoints to represent motion discontinuities [Reference Mathew, Taubman and Zanuttigh16]; breakpoints are very useful in a scalable video coder because of their high scalability attributes both in quality and resolution. See Section IV for more details on how breakpoints are employed in this work to induce motion discontinuities.
The first step of the proposed method consists of warping motion discontinuity information from reference frames f
a
and f
c
, to the (non-existent) target frame f
b
. Next, we compute an estimate
![]() $\hat{M}_{a \rightarrow b}$
of the motion field between frame f
a
and the target frame f
b
by scaling the parent motion field
$\hat{M}_{a \rightarrow b}$
of the motion field between frame f
a
and the target frame f
b
by scaling the parent motion field
![]() $M_{a \rightarrow c}$
by a factor of 0.5. Next, we infer a motion field
$M_{a \rightarrow c}$
by a factor of 0.5. Next, we infer a motion field
![]() $\hat{M}_{c \rightarrow b}$
, which is anchored at frame f
c
and pointing backwards to frame f
b
; to infer
$\hat{M}_{c \rightarrow b}$
, which is anchored at frame f
c
and pointing backwards to frame f
b
; to infer
![]() $\hat{M}_{c \rightarrow b}$
, both its temporal parent motion
$\hat{M}_{c \rightarrow b}$
, both its temporal parent motion
![]() $M_{a \rightarrow c}$
, and its temporal sibling
$M_{a \rightarrow c}$
, and its temporal sibling
![]() $\hat{M}_{a \rightarrow b}$
, are used.
$\hat{M}_{a \rightarrow b}$
, are used.
The next step is to invert both
![]() $\hat{M}_{a \rightarrow b}$
and
$\hat{M}_{a \rightarrow b}$
and
![]() $\hat{M}_{c \rightarrow b}$
, so that we obtain the two motion fields
$\hat{M}_{c \rightarrow b}$
, so that we obtain the two motion fields
![]() $\hat{M}_{b \rightarrow a}$
and
$\hat{M}_{b \rightarrow a}$
and
![]() $\hat{M}_{b \rightarrow c}$
, which are anchored at the target frame f
b
we want to interpolate. During this inversion process, we readily observe regions of the motion that are getting disoccluded; such regions are recorded in the disocclusion masks
$\hat{M}_{b \rightarrow c}$
, which are anchored at the target frame f
b
we want to interpolate. During this inversion process, we readily observe regions of the motion that are getting disoccluded; such regions are recorded in the disocclusion masks
![]() $\hat{S}_{b \rightarrow a}$
and
$\hat{S}_{b \rightarrow a}$
and
![]() $\hat{S}_{b \rightarrow c}$
, and are used to guide the bidirectional, occlusion-aware motion-compensated temporal frame interpolation (MCTFI) process.
$\hat{S}_{b \rightarrow c}$
, and are used to guide the bidirectional, occlusion-aware motion-compensated temporal frame interpolation (MCTFI) process.
III. BIDIRECTIONAL HIERARCHICAL ANCHORING OF MOTION FIELDS
All current state-of-the-art video codecs anchor motion fields at the target frames. In [Reference Rüfenacht, Mathew and Taubman17], we proposed to anchor motion fields at the reference frames instead. In this paper, we demonstrate how the underlying methods of constructing motion fields are highly suited for FI, and can lead to a geometrically consistent bidirectional prediction of the interpolated target frames. Perhaps surprisingly, these interpolated frames can have higher quality than those produced by state-of-the-art TFI schemes. Figure 2 shows the two different ways of anchoring motion fields.

Fig. 2. (a) Traditional anchoring of motion fields in the target frames and (b) bidirectional hierarchical anchoring (BIHA) of motion fields at reference frames.
Let us assume that all odd frames (f
b
and f
d
in Fig. 2) are not present at the encoder, and we want to interpolate them at the decoder. In that case,
![]() $M_{a \rightarrow c}$
is the only motion field present at the decoder that can (potentially) be useful to interpolate frame f
b
. In current state-of-the-art codecs,
$M_{a \rightarrow c}$
is the only motion field present at the decoder that can (potentially) be useful to interpolate frame f
b
. In current state-of-the-art codecs,
![]() $M_{a \rightarrow c}$
is a block-based prediction field that minimizes the prediction residual, and is not reflective of “true motion”. As a result,
$M_{a \rightarrow c}$
is a block-based prediction field that minimizes the prediction residual, and is not reflective of “true motion”. As a result,
![]() $M_{a \rightarrow c}$
cannot be scaled to point to the intermediate frame f
b
, and hence has to be (re)estimated at the decoder. In our scalable video coding scheme, we closely model “true” motion fields, which can be scaled and hence readily be used to perform FI at the decoder.
$M_{a \rightarrow c}$
cannot be scaled to point to the intermediate frame f
b
, and hence has to be (re)estimated at the decoder. In our scalable video coding scheme, we closely model “true” motion fields, which can be scaled and hence readily be used to perform FI at the decoder.
With a “true” motion field
![]() $M_{a \rightarrow c}$
, one can readily compute a scaled version that points to the intermediate frame f
b
, as
$M_{a \rightarrow c}$
, one can readily compute a scaled version that points to the intermediate frame f
b
, as
![]() $\hat{M}_{a \rightarrow b} = \alpha M_{a \rightarrow c}$
(typically α=0.5). In order to serve as prediction reference to interpolate frame f
b
, we need to invert
$\hat{M}_{a \rightarrow b} = \alpha M_{a \rightarrow c}$
(typically α=0.5). In order to serve as prediction reference to interpolate frame f
b
, we need to invert
![]() $\hat{M}_{a \rightarrow b}$
. We present how motion fields are inverted for this work in {Section V.A}. Around the moving object boundaries, there will be regions that get disoccluded (e.g., uncovered) from frame f
a
to f
b
; such regions cannot be predicted from f
a
. It is highly likely that such regions are visible in frame f
c
, that is why we are interested in obtaining
$\hat{M}_{a \rightarrow b}$
. We present how motion fields are inverted for this work in {Section V.A}. Around the moving object boundaries, there will be regions that get disoccluded (e.g., uncovered) from frame f
a
to f
b
; such regions cannot be predicted from f
a
. It is highly likely that such regions are visible in frame f
c
, that is why we are interested in obtaining
![]() $M_{c \rightarrow b}$
.
$M_{c \rightarrow b}$
.
One could be tempted to estimate
![]() $M_{c \rightarrow a}$
, and then compute
$M_{c \rightarrow a}$
, and then compute
![]() $M_{c \rightarrow b}$
as a scaled version of
$M_{c \rightarrow b}$
as a scaled version of
![]() $M_{c \rightarrow a}$
. We avoid this strategy for two main reasons:
$M_{c \rightarrow a}$
. We avoid this strategy for two main reasons:
-
(i) In a highly scalable video coder, this would be redundant information.
-
(ii) It is very likely that
 $M_{a \rightarrow c} \neq (M_{c \rightarrow a})^{-1}$
, in particular around the moving objects. Hence, their scaled versions will not be geometrically consistent in frame f
b
.
$M_{a \rightarrow c} \neq (M_{c \rightarrow a})^{-1}$
, in particular around the moving objects. Hence, their scaled versions will not be geometrically consistent in frame f
b
.
We instead infer
![]() $\hat{M}_{c \rightarrow b}$
, anchored at frame f
c
, from the forward pointing motion field
$\hat{M}_{c \rightarrow b}$
, anchored at frame f
c
, from the forward pointing motion field
![]() $M_{a \rightarrow c}$
and its scaled version
$M_{a \rightarrow c}$
and its scaled version
![]() $\hat{M}_{a \rightarrow b}$
, as follows:
$\hat{M}_{a \rightarrow b}$
, as follows:
where ∘ denotes the composition operator. The fact that
![]() $M_{c \rightarrow b}$
is completely defined by
$M_{c \rightarrow b}$
is completely defined by
![]() $M_{a \rightarrow c}$
and
$M_{a \rightarrow c}$
and
![]() $M_{a \rightarrow b}$
has the key advantage that
$M_{a \rightarrow b}$
has the key advantage that
![]() $M_{c \rightarrow b}$
always “follows”
$M_{c \rightarrow b}$
always “follows”
![]() $M_{a \rightarrow b}$
, such that the two motion fields involved in the prediction of frame f
b
are geometrically consistent. This highly desirable property is illustrated in Fig. 3. In practice, what this means is that the predicted target frame will be significantly less blurred and contain less ghosting than traditional TFI approaches; for examples, the reader is referred to Fig. 11. We remind the reader that a key principle in this work is to avoid averaging techniques (such as OBMC) that do not correspond to physical motion.
$M_{a \rightarrow b}$
, such that the two motion fields involved in the prediction of frame f
b
are geometrically consistent. This highly desirable property is illustrated in Fig. 3. In practice, what this means is that the predicted target frame will be significantly less blurred and contain less ghosting than traditional TFI approaches; for examples, the reader is referred to Fig. 11. We remind the reader that a key principle in this work is to avoid averaging techniques (such as OBMC) that do not correspond to physical motion.

Fig. 3. A rectangle moves from left to right, with accelerated motion. (a) shows the true location of the rectangle (green), and (b) the predicted position of the rectangle under constant motion assumption. Note that because the inferred motion (orange dashed line) follows the scaled motion (blue dotted), the two motion fields M̂ a→b and M̂ c→b are geometrically consistent.
IV. HIERARCHICAL WARPING OF MOTION FIELD DISCONTINUITIES
One key distinguishing feature of the proposed scheme is the use of motion discontinuity information to reason about scene geometry; it is used during the inversion of motion fields to resolve double mappings in regions of motion field folding (see Section V.A), as well as to extrapolate motion in disoccluded regions during the motion field inference process to obtain
![]() $\hat{M}_{c \rightarrow b}$
(see Section V.B). As this work builds upon an HSVC framework, we use a highly scalable way of coding discontinuities using breakpoints
Footnote
2
, where they are used to modify the behavior of the discrete wavelet transform (DWT) in the vicinity of (motion) discontinuities. In essence, the presence and precision of breakpoints in the hierarchical representation is determined in a rate-distortion optimized way; the interested reader is referred [Reference Mathew, Taubman and Zanuttigh16] for a much more detailed description of the technical details on the estimation of breakpoints. In the following, we give a brief summary of how breakpoints are used to induce motion discontinuities. We then present how breakpoints can be transferred from reference frames to the target frame we want to interpolate.
$\hat{M}_{c \rightarrow b}$
(see Section V.B). As this work builds upon an HSVC framework, we use a highly scalable way of coding discontinuities using breakpoints
Footnote
2
, where they are used to modify the behavior of the discrete wavelet transform (DWT) in the vicinity of (motion) discontinuities. In essence, the presence and precision of breakpoints in the hierarchical representation is determined in a rate-distortion optimized way; the interested reader is referred [Reference Mathew, Taubman and Zanuttigh16] for a much more detailed description of the technical details on the estimation of breakpoints. In the following, we give a brief summary of how breakpoints are used to induce motion discontinuities. We then present how breakpoints can be transferred from reference frames to the target frame we want to interpolate.
A) Inducing motion discontinuities from breakpoints
This section presents how motion discontinuity information can be induced from an existing breakpoint field; for a comprehensive description of how breakpoints used in this work are estimated, we refer the interested reader to [Reference Mathew, Taubman and Zanuttigh16]. Breakpoints lie on grid arcs, and can be connected to form discontinuity line segments. They are organized in a hierarchical manner, such that breakpoints at finer spatial levels can be induced from coarser levels. We use Fig. 4 to guide the description.

Fig. 4. Scalable geometry representation: Two breakpoints on the perimeter of the same cell can induce discontinuity information onto the root arcs (purple crosses). If the root arc contains a vertex (red cross), the inducing is stopped.
A breakpoint field at spatial level η consists of cells of size
![]() $2^{\eta} \times 2^{\eta}$
pixels; these cells are the fundamental unit used to induce discontinuities. A cell consists of four perimeter arcs (cyan lines in Fig. 4), as well as two root arcs (gray lines in Fig. 4). The significance of root arcs is that they do not exist at coarser levels in the pyramid. Each arc can be occupied by at most one breakpoint. If a cell contains exactly two perimeter breakpoints, and the root arcs at this level have no explicitly coded breaks, connecting the two perimeter breaks allows breakpoints to be induced onto the root arcs. To avoid confusion, we use the term vertices to identify the explicitly coded breaks. What this means then is that spatial induction transfers discontinuity information recursively from coarser level vertices to finer levels in the hierarchy, except where such transfer would be in conflict with finer level vertices.
$2^{\eta} \times 2^{\eta}$
pixels; these cells are the fundamental unit used to induce discontinuities. A cell consists of four perimeter arcs (cyan lines in Fig. 4), as well as two root arcs (gray lines in Fig. 4). The significance of root arcs is that they do not exist at coarser levels in the pyramid. Each arc can be occupied by at most one breakpoint. If a cell contains exactly two perimeter breakpoints, and the root arcs at this level have no explicitly coded breaks, connecting the two perimeter breaks allows breakpoints to be induced onto the root arcs. To avoid confusion, we use the term vertices to identify the explicitly coded breaks. What this means then is that spatial induction transfers discontinuity information recursively from coarser level vertices to finer levels in the hierarchy, except where such transfer would be in conflict with finer level vertices.
B) Temporal breakpoint induction
For TFI, motion discontinuity information is not available for frame f b . In this work, we transfer such discontinuity information from the reference frames to the target frame using a hierarchical extension of the breakpoint warping scheme proposed in [Reference Rüfenacht, Mathew and Taubman18]. The underlying idea of mapping breakpoints from reference to target frames is the fact that motion discontinuities travel with the foreground object. Because the presence of a breakpoint necessarily implies that the motion on either side of it is significantly different, the aim is to identify the foreground motion by performing a breakpoint compatibility check between the two reference frames f a and f c , and then to warp compatible line segments to the target frame by halving the identified foreground motion. Figure 5 illustrates the three main steps of the proposed hierarchical temporal breakpoint induction method:
-
(i) Breakpoint compatibility check to find compatible (i.e., foreground) motion to assign to discontinuity line segments.
-
(ii) Warping of compatible line segments under constant motion assumption to the target frame, where they are intersected with grid arcs and stored as breakpoints (temporal induction).
-
(iii) Upsampling of breakpoints to the next finer spatial resolution (spatial induction).

Fig. 5. Spatio-temporal induction of breakpoints. Going from coarse to fine spatial resolution, the proposed temporal induction process consists of three steps at each resolution level η: (1) Assessment of temporal compatibility of line segments induced by breakpoints between two coarse-level frames f a and f c ; (2) Warping of compatible line segments to f b ; (3) Spatial induction of all breakpoints to the next finer spatial resolution η−1. For better visualization, root arcs are not shown in this figure.
In cases where a warped line segment intersects an arc that already contains a spatially induced breakpoint, the temporally induced breakpoint always overwrites the spatially induced one.
The advantage of this hierarchical extension is that the temporal inducing constraints are tightest at the finest spatial resolution; spatially induced discontinuity information from coarser spatial levels can help completing discontinuity information in regions that are not compatible at finer spatial resolutions.
V. MOTION FIELD OPERATIONS
In this section, we present two motion field operations that are used in the proposed TFI method, and show how motion discontinuity information is used to solve key problems current TFI methods suffer from, namely the handling of double mappings, as well as occluded regions.
A) Inversion of motion fields
Most TFI methods map either pixels or whole blocks from reference to target frames, which creates a variety of unwanted artifacts such as holes within objects because the adjacent blocks have different motion assigned. Also, even if ground truth motion were used, a simple mapping can lead to holes in the target frame if the object is expanding.
To avoid these problems, we employ piecewise-smooth motion, and employ a cellular affine warping (CAW) procedure first proposed in [Reference Rüfenacht, Mathew and Taubman18] to warp motion fields from one frame to another. We use Fig. 6 to guide the description of the CAW procedure. In the current implementation, the reference motion field is partitioned into triangles of size 1×1 pixel, so that there are approximately twice as many triangles as there are pixels in the frame.Footnote 3 The warped motion field is guaranteed to have no holes (in disoccluded regions). On the leading side of moving objects, one is likely to observe double mappings during the motion field warping process. In the following, we explain how such double mappings can be resolved using motion discontinuity information.

Fig. 6. Illustration of the proposed CAW procedure. These figures show color-coded motion fields. (a) The reference motion field is partitioned into triangles; (b) each such triangle is then mapped from the reference to the target frame, where each integer location gets assigned the corresponding affine motion. In regions that get disoccluded, triangles stretch without changing orientation (e.g., the green triangle), and the affine model assigns a interpolated value between the foreground and background motion, without leaving any hole.
1) Identifying foreground motion in double-mapped regions
As explained in the previous section, as the CAW procedure maps triangles from reference to target frames, in regions of folding, multiple triangles map to the same location x
j
in the target frame f
j
. In other words, there are two locations
![]() ${\bf x}_{i,1}$
and
${\bf x}_{i,1}$
and
![]() ${\bf x}_{i,2}$
in f
i
, which are mapped by
${\bf x}_{i,2}$
in f
i
, which are mapped by
![]() $M_{i \rightarrow j}$
to the same location. In this section, we show how motion discontinuity information can be used to locally reason about foreground moving objects. We use Fig. 7 to guide the description. We denote the line segment that connects
$M_{i \rightarrow j}$
to the same location. In this section, we show how motion discontinuity information can be used to locally reason about foreground moving objects. We use Fig. 7 to guide the description. We denote the line segment that connects
![]() ${\bf x}_{i,1}$
and
${\bf x}_{i,1}$
and
![]() ${\bf x}_{i,2}$
in the reference frame f
i
as
${\bf x}_{i,2}$
in the reference frame f
i
as
![]() ${\bf l}$
; this line has to intersect with (at least) one motion discontinuity, denoted as B in the figure. In the example, the scepter is lifted and moves on top of the snow in the background. Let B
− denote the location on
${\bf l}$
; this line has to intersect with (at least) one motion discontinuity, denoted as B in the figure. In the example, the scepter is lifted and moves on top of the snow in the background. Let B
− denote the location on
![]() ${\bf l}$
which is on the same side as
${\bf l}$
which is on the same side as
![]() ${\bf x}_{i,1}$
; similarly, let B
+ denote the location on
${\bf x}_{i,1}$
; similarly, let B
+ denote the location on
![]() ${\bf l}$
that is on the side of
${\bf l}$
that is on the side of
![]() ${\bf x}_{i,2}$
. Because the motion discontinuity moves with the foreground object, either
${\bf x}_{i,2}$
. Because the motion discontinuity moves with the foreground object, either
![]() ${\bf y}_{j,{\bf B^{-}}} = M_{i \rightarrow j}({\bf B^{-}})$
{or}
${\bf y}_{j,{\bf B^{-}}} = M_{i \rightarrow j}({\bf B^{-}})$
{or}
![]() ${\bf y}_{j,{\bf B^{+}}} = M_{i \rightarrow j}({\bf B^{+}})$
will map very closely to a motion discontinuity in the target frame f
j
; this is the foreground motion we register. In the example in the figure,
${\bf y}_{j,{\bf B^{+}}} = M_{i \rightarrow j}({\bf B^{+}})$
will map very closely to a motion discontinuity in the target frame f
j
; this is the foreground motion we register. In the example in the figure,
![]() ${\bf y}_{j,{\bf B^{-}}}$
gets mapped onto motion discontinuities; therefore,
${\bf y}_{j,{\bf B^{-}}}$
gets mapped onto motion discontinuities; therefore,
![]() $\hat{M}_{a \rightarrow b}({\bf x}_{i,1})$
gets recorded as foreground motion at location
$\hat{M}_{a \rightarrow b}({\bf x}_{i,1})$
gets recorded as foreground motion at location
![]() ${\bf x}_{j}$
where the double mapping occurred (e.g.,
${\bf x}_{j}$
where the double mapping occurred (e.g.,
![]() $\hat{M}_{b \rightarrow a}({\bf x}_{j}) = - \hat{M}_{a \rightarrow b}({\bf x}_{i,1})$
).
$\hat{M}_{b \rightarrow a}({\bf x}_{j}) = - \hat{M}_{a \rightarrow b}({\bf x}_{i,1})$
).

Fig. 7. Resolving of double mappings in the mapped motion field by reasoning about motion discontinuities (represented as red dashed lines around the scepter). The key idea in identifying the foreground motion is that the motion discontinuities travel with the foreground object.
2) Obtaining a disocclusion mask
The inversion of
![]() $M_{i \rightarrow j}$
allows us to readily observe regions that get disoccluded in the target frame; we record this valuable information in a disocclusion mask
$M_{i \rightarrow j}$
allows us to readily observe regions that get disoccluded in the target frame; we record this valuable information in a disocclusion mask
![]() $S_{j \rightarrow i}$
as follows:
$S_{j \rightarrow i}$
as follows:
In the proposed bidirectional prediction setup, we obtain two such disocclusion masks anchored at the target frame f
b
: one during the inversion of
![]() $M_{a \rightarrow b}$
, which we denote
$M_{a \rightarrow b}$
, which we denote
![]() $S_{b \rightarrow a}$
, and the other
$S_{b \rightarrow a}$
, and the other
![]() $S_{b \rightarrow c}$
, obtained during the inversion of
$S_{b \rightarrow c}$
, obtained during the inversion of
![]() $M_{c \rightarrow b}$
. They are used to generate the interpolated frame as explained in Section VI.
$M_{c \rightarrow b}$
. They are used to generate the interpolated frame as explained in Section VI.
B) Motion field inference
As shown in equation (1), the backward pointing motion field
![]() $\hat{M}_{c \rightarrow b}$
, anchored at frame f
c
, is inferred from the forward pointing motion field
$\hat{M}_{c \rightarrow b}$
, anchored at frame f
c
, is inferred from the forward pointing motion field
![]() $M_{a \rightarrow c}$
and its scaled version
$M_{a \rightarrow c}$
and its scaled version
![]() $\hat{M}_{a \rightarrow b}$
. As mentioned earlier, one advantage of this operation is that
$\hat{M}_{a \rightarrow b}$
. As mentioned earlier, one advantage of this operation is that
![]() $\hat{M}_{a \rightarrow b}$
and
$\hat{M}_{a \rightarrow b}$
and
![]() $\hat{M}_{c \rightarrow b}$
are geometrically consistent, meaning that the interpolated target frame will contain much less ghosting artifacts.
$\hat{M}_{c \rightarrow b}$
are geometrically consistent, meaning that the interpolated target frame will contain much less ghosting artifacts.
Both
![]() $\hat{M}_{a \rightarrow b}$
and
$\hat{M}_{a \rightarrow b}$
and
![]() $\hat{M}_{c \rightarrow b}$
should reflect “true” motion with sharp discontinuities. In particular,
$\hat{M}_{c \rightarrow b}$
should reflect “true” motion with sharp discontinuities. In particular,
![]() $\hat{M}_{c \rightarrow b}$
is most useful in regions which are not visible in frame f
a
(e.g., disoccluded). Part of the motion field inference process involves the inversion of the motion field
$\hat{M}_{c \rightarrow b}$
is most useful in regions which are not visible in frame f
a
(e.g., disoccluded). Part of the motion field inference process involves the inversion of the motion field
![]() $M_{a \rightarrow c}$
; during this process, we readily observe regions that are not visible in f
a
. The CAW procedure assigns a linear interpolation between background and foreground motion to disoccluded regions; in order to be most useful, however, motion in disoccluded regions of
$M_{a \rightarrow c}$
; during this process, we readily observe regions that are not visible in f
a
. The CAW procedure assigns a linear interpolation between background and foreground motion to disoccluded regions; in order to be most useful, however, motion in disoccluded regions of
![]() $\hat{M}_{c \rightarrow b}$
should be extrapolated from the triangle vertices falling on one side of the motion discontinuities. In the following, we describe this procedure in more detail.
$\hat{M}_{c \rightarrow b}$
should be extrapolated from the triangle vertices falling on one side of the motion discontinuities. In the following, we describe this procedure in more detail.
1) Motion extrapolation in disoccluded triangles
The aim of the motion inference process is to obtain a motion field
![]() $\hat{M}_{c \rightarrow b}$
, anchored at frame f
c
, and pointing to f
b
, which is as close to a “real” motion field as possible. In the absence of new motion appearing in regions that get disoccluded between frames f
a
and f
c
, a good estimate for the motion is to extrapolate the motion of the triangle vertices up to motion discontinuity boundaries. For most of the disoccluded triangle, this means that background motion is extrapolated; only a small (if any) part of the triangle falls onto the foreground object. We use Fig. 8 to explain the details of the proposed motion extrapolation technique.
$\hat{M}_{c \rightarrow b}$
, anchored at frame f
c
, and pointing to f
b
, which is as close to a “real” motion field as possible. In the absence of new motion appearing in regions that get disoccluded between frames f
a
and f
c
, a good estimate for the motion is to extrapolate the motion of the triangle vertices up to motion discontinuity boundaries. For most of the disoccluded triangle, this means that background motion is extrapolated; only a small (if any) part of the triangle falls onto the foreground object. We use Fig. 8 to explain the details of the proposed motion extrapolation technique.

Fig. 8. Closeup of the scene in Fig. 6, to illustrate the motion extrapolation technique applied in disoccluded regions. Panel (a) shows a triangle in the reference frame f i , which straddles a motion discontinuity boundary. Panel (b) shows the warped, stretched triangle in the target frame f j ; panel (c) introduces the relevant notations used in the text to describe the motion extrapolation procedure. Instead of linearly interpolating motion from foreground to background, we instead extrapolate motion from the vertices to the motion discontinuity boundary, represented by B 1 and B 2; this results in sharp boundaries, as exemplified in (d), where the blue dotted line corresponds to linearly interpolated motion, and the green solid line corresponds to extrapolated motion.
Whenever a triangle is stretching as it is mapped from a reference to a target frame, we expect it to intersect with motion discontinuities in the target frame; this is because some of its vertices belong to the background (possibly in motion), and some belong to the foreground (moving) object. In Fig. 8(c),
![]() $D_{1}^{\prime}$
and
$D_{1}^{\prime}$
and
![]() $D_{2}^{\prime}$
sit in the background, whereas
$D_{2}^{\prime}$
sit in the background, whereas
![]() $D_{3}^{\prime}$
belongs to the foreground. The warped triangle has two edges that intersect with motion discontinuities, which we denote as e
1 and e
2. As mentioned before, instead of interpolating a value transitioning from background (
$D_{3}^{\prime}$
belongs to the foreground. The warped triangle has two edges that intersect with motion discontinuities, which we denote as e
1 and e
2. As mentioned before, instead of interpolating a value transitioning from background (
![]() $D_{1}^{\prime}$
in Fig. 8) to the foreground motion
$D_{1}^{\prime}$
in Fig. 8) to the foreground motion
![]() $D_{3}^{\prime}$
, we want to extrapolate the background motion up to the motion boundary, and likewise extrapolate the foreground motion up to the motion boundary. To clarify this, we show a 1D cut along the e
1, formed by connecting
$D_{3}^{\prime}$
, we want to extrapolate the background motion up to the motion boundary, and likewise extrapolate the foreground motion up to the motion boundary. To clarify this, we show a 1D cut along the e
1, formed by connecting
![]() $D_{1}^{\prime}$
and
$D_{1}^{\prime}$
and
![]() $D_{3}^{\prime}$
, of the horizontal component (mv
x
) of the motion in Fig. 8(d); the dashed blue line shows the motion assigned by the CAW procedure, and the green solid (staircase) shows the background and foreground extrapolated motion. Irrespective of what object (foreground or background) each of the three vertices of the triangle belongs to, the motion extrapolation method performs the same steps: The motion of
$D_{3}^{\prime}$
, of the horizontal component (mv
x
) of the motion in Fig. 8(d); the dashed blue line shows the motion assigned by the CAW procedure, and the green solid (staircase) shows the background and foreground extrapolated motion. Irrespective of what object (foreground or background) each of the three vertices of the triangle belongs to, the motion extrapolation method performs the same steps: The motion of
![]() $D_{3}^{\prime}$
is extrapolated in the triangle formed by
$D_{3}^{\prime}$
is extrapolated in the triangle formed by
![]() $D_{1}^{\prime}$
, B
1, and B
2. The quadrilateral (
$D_{1}^{\prime}$
, B
1, and B
2. The quadrilateral (
![]() $D_{1}^{\prime}$
,
$D_{1}^{\prime}$
,
![]() $D_{2}^{\prime}$
, B
1, B
2) is broken up into two triangles (
$D_{2}^{\prime}$
, B
1, B
2) is broken up into two triangles (
![]() $D_{1}^{\prime}$
,
$D_{1}^{\prime}$
,
![]() $D_{2}^{\prime}$
, B
1) and (
$D_{2}^{\prime}$
, B
1) and (
![]() $D_{2}^{\prime}$
, B
1, B
2), and the motion of
$D_{2}^{\prime}$
, B
1, B
2), and the motion of
![]() $D_{1}^{\prime}$
and
$D_{1}^{\prime}$
and
![]() $D_{2}^{\prime}$
is extrapolated in the respective triangles.
$D_{2}^{\prime}$
is extrapolated in the respective triangles.
VI. MOTION-COMPENSATED TEMPORAL FRAME INTERPOLATION
The last step is to interpolate the target frame f̂
b
. We use
![]() $\cal{W}_{\hat{M}_{i \rightarrow j}}(f_{j})$
to denote the warping process of frame f
j
to frame f
i
. The warping of frame f
j
to frame f
i
, evaluated at location x, is then denoted as
$\cal{W}_{\hat{M}_{i \rightarrow j}}(f_{j})$
to denote the warping process of frame f
j
to frame f
i
. The warping of frame f
j
to frame f
i
, evaluated at location x, is then denoted as
![]() $f_{j \rightarrow i}({\bf x}) = (\cal{W}_{\hat{M}_{i \rightarrow j}}(f_{j}))({\bf x})$
. Every pixel location
$f_{j \rightarrow i}({\bf x}) = (\cal{W}_{\hat{M}_{i \rightarrow j}}(f_{j}))({\bf x})$
. Every pixel location
![]() $\hat{f}_{b}({\bf x})$
in f
b
is computed using
$\hat{f}_{b}({\bf x})$
in f
b
is computed using
![]() $\hat{M}_{b \rightarrow a}$
and
$\hat{M}_{b \rightarrow a}$
and
![]() $\hat{M}_{b \rightarrow c}$
, together with the estimated disocclusion maps
$\hat{M}_{b \rightarrow c}$
, together with the estimated disocclusion maps
![]() $S_{b \rightarrow a}$
and
$S_{b \rightarrow a}$
and
![]() $S_{b \rightarrow c}$
, as:
$S_{b \rightarrow c}$
, as:
where
![]() $\kappa({\bf x})=S_{b \rightarrow a}({\bf x}) + S_{b \rightarrow c}({\bf x})$
.
$\kappa({\bf x})=S_{b \rightarrow a}({\bf x}) + S_{b \rightarrow c}({\bf x})$
.
Regions in f
b
which are disoccluded in both of the reference frames (i.e.,
![]() $\kappa({\bf x})=0$
), are predicted from both reference frames equally, where the affine warping process results in a stretching of the background texture information.
$\kappa({\bf x})=0$
), are predicted from both reference frames equally, where the affine warping process results in a stretching of the background texture information.
VII. ESTIMATION OF PIECEWISE-SMOOTH MOTION FIELDS WITH DISCONTINUITIES
In the proposed work, we require piecewise-smooth motion fields with sharp discontinuities at moving object boundaries. The estimation of such motion fields that are tailored for the proposed scheme is a parallel, ongoing stream of research. To show the applicability of the proposed scheme on natural sequences, we need to estimate motion fields that satisfy our requirements. We found that Xu et al.’s [Reference Xu, Jia and Matsushita14] motion detail preserving (MDP) optical flow algorithm provides motion fields of sufficient quality to work with our proposed framework; the parent motion field
![]() $\hat{M}_{a \rightarrow c}$
is estimated using the default parameters of their implementation.
$\hat{M}_{a \rightarrow c}$
is estimated using the default parameters of their implementation.
MDP uses an extended coarse-to-fine refinement framework, which is able to recover motion details at each scale by reducing the reliance of flow estimates that are propagated from coarser scales. Large displacements are handled by using sparse feature detection and matching, and a dense nearest-neighbor patch matching algorithm is used to handle small textureless regions which are likely missed by the feature matching algorithm. Furthermore, an adaptive structure map which maintains motion discontinuity is used in the optical flow regularization term.
Next, we run Mathew et al.’s [Reference Mathew, Taubman and Zanuttigh16] breakpoint estimation scheme to estimate motion discontinuities on
![]() $\hat{M}_{a \rightarrow c}$
(see Section IV). Figure 9 shows an example estimated motion and breakpoint field. To show the applicability of the estimated motion and breakpoint field on natural sequences, we further show estimated disocclusion masks, inverted motion fields, as well as temporally interpolated frame f̂
b
.
$\hat{M}_{a \rightarrow c}$
(see Section IV). Figure 9 shows an example estimated motion and breakpoint field. To show the applicability of the estimated motion and breakpoint field on natural sequences, we further show estimated disocclusion masks, inverted motion fields, as well as temporally interpolated frame f̂
b
.

Fig. 9. Example results for estimated motion on a natural sequence with reasonably complex motion. Panel (a) shows the motion field M̂ a→c , estimated using [14] with the default parameters; Panel (b) shows the breakpoint field (at the second coarsest spatial level for visualization), which was estimated on M̂ a→c using the breakpoint estimation method described in [16]. Panel (c) shows the union of the estimated disocclusion masks, where yellow and cyan indicate that the pixel is not visible in the previous (f a ) and future (f c ) frame, respectively. Panels (d) and (e) show the inverted motion fields, anchored at the target frame f b , which together with the disocclusion mask are used to obtain (f), the bidirectionally predicted target frame f̂ b .
We note that in our wavelet-based highly scalable video coder [Reference Rüfenacht, Mathew and Taubman13], the motion field estimation and the breakpoint estimation is performed at the encoder; at the decoder, only the motion field inversion and subsequent motion-compensated prediction of the frame to be interpolated have to be performed, which significantly reduces the computational complexity of the proposed approach.
VIII. EXPERIMENTAL EVALUATION AND DISCUSSION
In our previous work [Reference Rüfenacht, Mathew and Taubman12], we have shown preliminary results of the proposed BOA-TFI method on synthetic sequences, and have highlighted the quality of the proposed method in occluded regions. In this work, we significantly enhance the evaluation of the proposed method both qualitatively and quantitatively on various high-resolution natural sequences (Section VIII.A), and compare our performance with two state-of-the-art TFI methods [Reference Jeong, Lee and Kim6,Reference Veselov and Gilmutdinov7].
One key distinguishing feature of the proposed method is its ability to handle regions around moving objects. Video resolution has seen a significant increase in recent years, while the frame-rate has not dramatically changed; what this means is that the expected size of disoccluded regions is larger, which makes appropriate handling of such regions more important. By contrast, the handling of occluded regions on low-resolution video (e.g., CIF and lower) is not so important, since they tend to be small. On such low-resolution sequences, our TFI method performs similarly to existing TFI methods, and sometimes even worse, because we do not apply any smoothing to our interpolated frames. In this paper, we want to highlight the importance of better motion and interpolation methods for high-resolution data; for this reason, all experiments are performed on high-resolution video sequences.
Recently, the computer-generated animation movie “Sintel” has become very popular in the computer vision community because of its complexity and high correlation with natural sequences [Reference Butler, Wulff, Stanley and Black19]; in Section VIII.C, we further show qualitative results of the proposed motion inference scheme on various scenes from the Sintel sequence, which contain much larger amounts of disocclusions than the natural sequences.
A) Results on natural sequences
In this section, we show the results obtained on common test sequences; motion fields are estimated using the optical flow estimator proposed by Xu et al. [Reference Xu, Jia and Matsushita14], as detailed in Section VII. We compare our results with two state-of-the-art TFI methods: Jeong et al.[Reference Jeong, Lee and Kim6] focus on a sophisticated multi-hypothesis testing framework, where a lot of effort is spent on texture optimization. Veselov and Gilmutdinov [Reference Veselov and Gilmutdinov7] focus on estimating high-quality motion fields, which are then used without any sophisticated texture optimization to interpolate the target frame.
We selected 12 sets of various common high-resolution test sequences with a large variety of motion and texture complexity; Fig. 10 shows the first frame of each sequence. For each such sequence, we choose 11 adjacent even numbered frames, and interpolate the odd numbered frames in between them; this results in 10 interpolated frames per sequence. Table 2 presents the per sequence results, averaged over the 10 frames.

Fig. 10. First frame of each of the natural sequences used in the experiments. All sequences are readily available on https://media.xiph.org/video/derf/.
Table 2. Quantitative comparison of the proposed method with [Reference Jeong, Lee and Kim6,Reference Veselov and Gilmutdinov7] on common natural test sequences. In parantheses (·), we show the difference between the PSNR of the proposed BOA-TFI method and the respective method we compare it with \newline (“−” means that the proposed BOA-TFI performs better, “+” means worse performance).

Bold indicates the best performance for a given sequence.
While reporting average peak signal-to-noise ratio (PSNR) values provides a compact way of summarizing the performance of the tested methods, we note that this measure only makes sense in regions where there is no acceleration between the two reference frames. Ultimately, it is the perceived visual quality that is important. We therefore provide qualitative results for some of the sequences in Fig. 11. First off, both TFI methods chosen for comparison are able to provide high-quality interpolated frames, in particular in regions inside moving objects (i.e., away from moving object boundaries). The differences in PSNR values and visual quality are governed by two major factors:

Fig. 11. Qualitative comparison of TFI on natural sequences. The first row shows the full frame. The second to last row show crops of the ground truth, proposed BOA-TFI, Jeong et al. [6] and Veselov and Gilmutdinov [7], respectively.
1) How regions of global motion are interpolated
Block-based methods usually employ a variant of OBMC, which tends to oversmooth the interpolated frames, resulting in significant blurring of the overall texture. In Fig. 11, this can be seen in highly textured regions such as the running man with the umbrella in the first column, as well as the text on the card of the Cactus sequence in the second row.
2) How regions around moving objects are handled
Regions around moving objects are only visible from one reference frame, and hence should only be predicted from the frame they are visible. This can only be achieved if such regions are detected. The quality of the proposed occlusion handling can be appreciated in various crops shown, but is most visible in the “Parkrun” sequence, as well as the “Cactus” sequence, where the “10” (cyan crop) is properly interpolated by our method.
In the current implementation of the proposed method, we do not perform any texture optimization. In regions which are highly affected by motion blur, such as the tiger in the “Cactus” sequence, this can create artificial high frequencies. A similar observation is also noted for the “Rushhour” sequence, which is highly affected by motion blur and atmospheric blur. For the first frames of the “Kimono” sequence, the optical flow estimator has problems on the right side of the woman, and mistakenly associates background pixels to the foreground object. While hardly visible, this results in a significant PSNR drop.
We plan to address the above-mentioned problems in future work by selectively smoothing the prediction in regions where there is a transition from uni- to bidirectional prediction; such regions can easily be identified by the presence of motion discontinuities.
B) Processing times
In this section, we report on the processing times of the proposed TFI method, and compare it with [Reference Jeong, Lee and Kim6,Reference Veselov and Gilmutdinov7]. It is important to note that none of the methods is optimized for time, and the timings were obtained on different machines. Table 3 shows the relevant specifications of the testing machines, as well as the average per-frame processing time. As mentioned before, we use [Reference Xu, Jia and Matsushita14] to estimate motion fields, and the contribution of this work is how such motion and estimated motion discontinuity information can be used to improve the FI process. For this reason, we split up the processing times for the ME part and the FI part.
Table 3. Average per-frame processing time (in sec) on all the frames tested in Section VIII.A, split up in ME and FI, as well as total time. We further provide the CPU and amount of RAM of the machines the results were obtained.
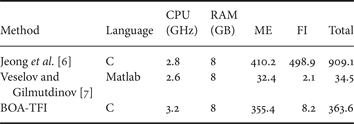
One can see that most of the processing time in the proposed BOA-TFI method is spent on estimating the motion, which is currently done using [Reference Xu, Jia and Matsushita14]. Veselov and Gilmutdinov [Reference Veselov and Gilmutdinov7] is about 10 times faster than the proposed method, while our BOA-TFI is around three times faster than Jeong et al. [Reference Jeong, Lee and Kim6].
We are working on an ME scheme that is tailored for the proposed method, which should make the ME both faster and more suited for the BOA-TFI scheme. Furthermore, in existing video codecs, the motion has to be (re-)estimated at the decoder for TFI purposes. This is in stark contrast to an HSVC scheme such as the one proposed in [Reference Rüfenacht, Mathew and Taubman13], which employs estimated “physical” motion, which does not have to be (re-)estimated at the decoder for TFI purposes; this significantly reduces the processing time of the proposed TFI framework.
As mentioned before, the focus of this paper is on the motion inference process, which is part of the FI. Most of the FI time is spent on mapping triangles from one frame to another in order to change invert and infer motion fields. In the current implementation, we map triangles of size 1×1; in regions away from moving objects, where motion is expected to be smooth, the triangle size could be greatly increased without any significant loss in quality. Initial investigations on a small number of sequences show that triangle merging can result in roughly 40–50 times fewer triangles, and hence a significant drop in the processing time can be expected. A much more thorough investigation of the trade-off between larger triangle size and interpolation quality is left for future work.
C) Results on Sintel sequences
As mentioned earlier, the main focus of this work is on the motion inference process which produces geometrically consistent interpolated frames. For this to work, we need piecewise-smooth motion fields with sharp boundaries at moving object boundaries. The optical flow estimator we currently use to generate the results in Section VIII.A ([Reference Xu, Jia and Matsushita14]) is unidirectional, and hence has problems in finding the “correct” object boundary on the side of moving objects which do not have a correspondence; a parallel stream of work on bidirectional ME schemes is likely to provide further improved results.
To substantiate this claim and show what the proposed scheme is capable of if motion fields better suited for our TFI method are employed, we turn our attention to the Sintel sequence [Reference Butler, Wulff, Stanley and Black19]; this computer-generated sequence is gaining a lot of popularity in the computer vision community because of its complexity. In order to show the performance of the scheme with “better” motion, we look at the quality of interpolated frames obtained using ground truth motion fields. Since both methods we compare ourselves to in Section VIII.A cannot make use of ground truth motion, we only show the results of our method, noting that any block-ME scheme would be highly challenged by the complexity of the underlying motion fields. Figure 12 shows sample interpolated frames generated by the proposed BOA-TFI method; full-resolution versions of the results, including animated versions, can be found on the website dedicated to this publication.Footnote 4

Fig. 12. TFI results on Sintel Sequence, which highlights the effectiveness of the proposed method to handle occluded regions. The first column shows the (color-coded) ground truth motion fields between the two reference frames, which, together with the two reference frames (not shown), form the input to our method in this experiment. The second column shows the union of the forward and backward disocclusion mask produced by the proposed BOA-TFI method, where yellow pixels are locations that get disoccluded between the previous and the interpolated frame; similarly, cyan are locations that get disoccluded between the future reference frame and the interpolated frame; red are regions that are not visible in either of the frames. The last column shows crops of the temporally interpolated frames obtained by the proposed BOA-TFI method.
The first column in the figure shows the (complex) ground truth motion fields, containing a variety of types of motion such as translation, rotation, zoom, and panning; furthermore, the motion magnitudes are much larger than on most natural sequences, resulting in larger regions of disocclusion around moving objects, as visualized in the second column of the figure. Because the ground truth motion fields for the Sintel sequence are only between adjacent frames, the frame we interpolate does not exist in the sequence, and hence we cannot compute a PSNR. As mentioned before, what ultimately counts is the perceived quality. One can see how the scheme is able to create high-quality reconstructed frames. The crops in the third row of Fig. 12 highlight difficult regions around moving object boundaries, where our BOA-TFI scheme switches from bidirectional to unidirectional prediction without smoothing the texture.
It is worth highlighting that the current scheme does not perform any texture optimization. In particular, the transition from uni- to bidirectional prediction can cause artifacts at the transition boundary if there are significant changes in illumination between the two reference frames. This can be observed in the right crop of the “Bandage 1” sequence Fig. 12l, most visible in the upper left part; the part of the wing which is brighter moves under the hand, and hence is only predicted from the left reference frame. The wing is significantly brighter in the left reference frame, and hence the bidirectionally predicted part of the wing is darker than the unidirectionally predicted part. We plan to address this problem by looking into ways of optimizing the texture in such regions, which are easily identified from the disocclusion mask, and apply a selective filter in such transition regions. Even without any texture optimizations, we show that a good motion inference scheme is highly competitive with state-of-the-art TFI methods.
IX. CONCLUSIONS AND FUTURE WORK
This paper presents a TFI framework that creates geometrically consistent interpolated frames; explicit handling of occluded regions allows to resolve traditionally problematic regions around moving object boundaries. This is made possible by using high-quality piecewise-smooth motion fields, together with motion discontinuities at moving object boundaries. Motion discontinuities allow to reason about where foreground objects move, and enables to resolve double mappings, as well as assign reasonable motion in disoccluded regions.
We evaluate the method on a large set of natural and challenging computer-generated sequences, and our method compares favorably to state-of-the-art TFI methods. While the estimation and interpolation steps can be applied directly to the output from any current video codec, the proposed approach is especially beneficial if used in conjunction with a highly scalable video coder that employs the motion and breakpoint fields directly. In this case, the proposed method can be understood as an extension of the decoding algorithm, avoiding the need for (re)estimation of motion.
Ongoing and future work includes the development of a hierarchical ME scheme that is tailored to the proposed motion inference scheme. Furthermore, we plan to look into texture optimizations such as optical blur handling to further improve the visual quality of the upsampled frames.
ACKNOWLEDGEMENTS
We would like to thank Seong-Qyun Jeong [6] and Anton Veselov [7], for providing us with the results of their temporal frame interpolation methods.
Dominic Rüfenacht received his B.Sc. in Communication Systems, in 2009, and the M.Sc. in Communication Systems with specialization in “Signals, Images and Interfaces” in 2011, both from the Swiss Federal Institute of Technology in Lausanne (EPFL). During his undergraduate studies, he was an exchange student at the University of Waterloo, Ontario, Canada, and did his Master's thesis at Philips Consumer Lifestyle in Eindhoven, Netherlands, entitled “Stereoscopic High Dynamic Range Video”. From 2011 to 2013, he was with the Image and Visual Representation Group (IVRG) at EPFL as a Research Engineer, where he was working on computational photography problems, with emphasis on color and near-infrared imaging. He is currently pursuing a Ph.D. in Electrical Engineering at the University of New South Wales (UNSW), Sydney, Australia. His research interests are both in computational photography and highly scalable image and video compression.
Reji Mathew received the B.E. degree from the University of Western Australia, Perth, Australia, in 1990, and the M.E. and Ph.D. degrees from the University of New South Wales (UNSW), Australia, in 1996 and 2010, respectively. He is currently with UNSW where he pursues his research interests in image and video coding, motion estimation, and scalable representations of motion and depth data. Reji's prior work experience includes employment with UNSW, Canberra (ADFA), from 1996 to 1997, Motorola Labs, Motorola Australian Research Centre, Sydney, from 1997 to 2003, and National ICT Australia, Sydney, from 2004 to 2005.
David Taubman received B.S. and B.E. (Electrical) degrees in 1986 and 1988 from the University of Sydney, and M.S. and Ph.D. degrees in 1992 and 1994 from the University of California at Berkeley. From 1994 to 1998 he worked at Hewlett-Packard's Research Laboratories in Palo Alto, California, joining the University of New South Wales in 1998, where he is a Professor in the School of Electrical Engineering and Telecommunications. Dr. Taubman is author with M. Marcellin of the book, “JPEG2000: Image compression fundamentals, standards and practice”. His research interests include highly scalable image and video compression, motion estimation and modeling, inverse problems in imaging, perceptual modeling, and multimedia distribution systems. Dr. Taubman was awarded the University Medal from the University of Sydney. He has received two Best Paper awards: from the IEEE Circuits and Systems Society for the 1996 paper, “A Common Framework for Rate and Distortion Based Scaling of Highly Scalable Compressed Video”; and from the IEEE Signal Processing Society for the 2000 paper, “High Performance Scalable Image Compression with EBCOT”.
















