Article contents
Shock train response to pulse backpressure forcing
Published online by Cambridge University Press: 17 January 2024
Abstract
Transient numerical simulations were conducted to investigate the influence of large amplitude and fast impact backpressure on a shock train. The fundamental problem consists of a shock train within a constant-area channel with a Ma=1.61 inflow and a pulse backpressure applied to the outlet. The pressure disturbance in the isolator has an intense forcing-response lag. From the moment of the backpressure peak appearance, it takes 36 times the backpressure duration for the pressure disturbance to reach the upstream end. It moves upstream with time in the form of a normal shock wave. As time progresses, the normal shock degenerates into a 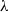 $\lambda $ shock and a compression wave behind due to the action of viscous dissipation in the boundary layer. Eventually, a multi-stage shock train is formed. The maximum backpropagation distance is a quadratic function of both the pulse backpressure peak and duration, and the relationship between these variables was determined by fitting. When the integral value of backpressure to time is fixed, reducing the backpressure peak while increasing the duration will reduce the backpressure pulsation at the isolator outlet, which will be more conducive to shortening the maximum backpropagation distance than reducing the duration and increasing the backpressure peak. The values of backpressure peak and duration are obtained from the detonation combustion case, which ensures the authenticity of backpressure characteristics. The relevant research conclusions can provide a reference for the design of the isolator of pulse detonation ramjet.
$\lambda $ shock and a compression wave behind due to the action of viscous dissipation in the boundary layer. Eventually, a multi-stage shock train is formed. The maximum backpropagation distance is a quadratic function of both the pulse backpressure peak and duration, and the relationship between these variables was determined by fitting. When the integral value of backpressure to time is fixed, reducing the backpressure peak while increasing the duration will reduce the backpressure pulsation at the isolator outlet, which will be more conducive to shortening the maximum backpropagation distance than reducing the duration and increasing the backpressure peak. The values of backpressure peak and duration are obtained from the detonation combustion case, which ensures the authenticity of backpressure characteristics. The relevant research conclusions can provide a reference for the design of the isolator of pulse detonation ramjet.
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of Royal Aeronautical Society
References
- 1
- Cited by

