Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Tuominen, Pekka
and
Tweedie, Richard L.
1979.
Exponential ergodicity in Markovian queueing and dam models.
Journal of Applied Probability,
Vol. 16,
Issue. 04,
p.
867.
Rubinovitch, Michael
and
Cohen, J. W.
1980.
Level crossings and stationary distributions for general dams.
Journal of Applied Probability,
Vol. 17,
Issue. 01,
p.
218.
Brockwell, P. J.
and
Pacheco-Santiago, N.
1980.
Invariant imbedding and dams with Markovian input rate.
Journal of Applied Probability,
Vol. 17,
Issue. 03,
p.
778.
Brockwell, P. J.
Resnick, S. I.
and
Tweedie, R. L.
1982.
Storage processes with general release rule and additive inputs.
Advances in Applied Probability,
Vol. 14,
Issue. 2,
p.
392.
Brockwell, P. J.
Resnick, S. I.
and
Pacheco-Santiago, N.
1982.
Extreme values, range and weak convergence of integrals of Markov chains.
Journal of Applied Probability,
Vol. 19,
Issue. 02,
p.
272.
Brockwell, P. J.
Resnick, S. I.
and
Pacheco-Santiago, N.
1982.
Extreme values, range and weak convergence of integrals of Markov chains.
Journal of Applied Probability,
Vol. 19,
Issue. 2,
p.
272.
Brockwell, P. J.
Gani, J. M.
and
Resnick, S. I.
1983.
CATASTROPHE PROCESSES WITH CONTINUOUS STATE‐SPACE1.
Australian Journal of Statistics,
Vol. 25,
Issue. 2,
p.
208.
Sato, Ken-iti
and
Yamazato, Makoto
1984.
Operator-selfdecomposable distributions as limit distributions of processes of Ornstein-Uhlenbeck type.
Stochastic Processes and their Applications,
Vol. 17,
Issue. 1,
p.
73.
de Kok, A.G.
1985.
Computational results for a dam problem with variable release rate and service level constraints.
Communications in Statistics. Stochastic Models,
Vol. 1,
Issue. 3,
p.
291.
Pötzelberger, Klaus
1987.
Completely positive operators and processes of Ornstein-Uhlenbeck type.
Stochastic Processes and their Applications,
Vol. 25,
Issue. ,
p.
249.
Perry, David
and
Posner, M. J. M.
1990.
Analysis of production/inventory systems with several production rates.
Communications in Statistics. Stochastic Models,
Vol. 6,
Issue. 1,
p.
99.
Zakusilo, O. K.
1990.
General Storage Processes with Additive Inputs.
Theory of Probability & Its Applications,
Vol. 34,
Issue. 2,
p.
240.
Zakusilo, O. K.
1991.
Once More on the Local Behavior of Storage Processes with Stable Input.
Theory of Probability & Its Applications,
Vol. 35,
Issue. 2,
p.
393.
Meyn, Sean P.
and
Tweedie, R. L.
1993.
Stability of Markovian processes III: Foster–Lyapunov criteria for continuous-time processes.
Advances in Applied Probability,
Vol. 25,
Issue. 03,
p.
518.
Bar-Lev, Shaul K.
and
Perry, David
1993.
Two-Stage Release Rule Procedure in a Regenerative Dam.
Probability in the Engineering and Informational Sciences,
Vol. 7,
Issue. 4,
p.
571.
Attia, F. A.
and
Brockwell, P. J.
1993.
On the control of an infinite capacity storage system.
Stochastic Hydrology and Hydraulics,
Vol. 7,
Issue. 3,
p.
195.
Zakusilo, O. K.
2000.
A Remark on the Characterization of the Global Behavior of a Process with Independent Increments.
Ukrainian Mathematical Journal,
Vol. 52,
Issue. 9,
p.
1380.
Löpker, Andreas
and
Palmowski, Zbigniew
2013.
On time reversal of piecewise deterministic Markov processes.
Electronic Journal of Probability,
Vol. 18,
Issue. none,
Daw, Andrew
Hampshire, Robert C.
and
Pender, Jamol J.
2025.
How to Staff When Customers Arrive in Batches.
Management Science,
Vol. 71,
Issue. 8,
p.
6580.
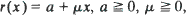 and when r(x) = x α and {A t } is stable with index β ∊ (0, 1). In general if EAt , < ∞ and r(0 +) > 0 it is shown that the condition sup r(x)>EA 1 is necessary and sufficient for a stationary distribution to exist, a stationary distribution being found explicitly when the conditions are satisfied. If sup r(x)>EA 1 it is shown that there is at most one stationary distribution and that if there is one then it is the limiting distribution of {Xt } as t → ∞. For {At } stable with index β and r(x) = x α , α + β = 1, we show also that
and when r(x) = x α and {A t } is stable with index β ∊ (0, 1). In general if EAt , < ∞ and r(0 +) > 0 it is shown that the condition sup r(x)>EA 1 is necessary and sufficient for a stationary distribution to exist, a stationary distribution being found explicitly when the conditions are satisfied. If sup r(x)>EA 1 it is shown that there is at most one stationary distribution and that if there is one then it is the limiting distribution of {Xt } as t → ∞. For {At } stable with index β and r(x) = x α , α + β = 1, we show also that 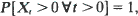 complementing results of Brockwell and Chung for the zero-set of {Xt } in the cases α + β < 1 and α + β > 1. We conclude with a brief treatment of the finite dam, regarded as a limiting case of infinite dams with suitably chosen release functions.
complementing results of Brockwell and Chung for the zero-set of {Xt } in the cases α + β < 1 and α + β > 1. We conclude with a brief treatment of the finite dam, regarded as a limiting case of infinite dams with suitably chosen release functions.
