In the study of ribbon knots, Lamm introduced symmetric unions inspired by earlier work of Kinoshita and Terasaka. We show an identity between the twisted Alexander polynomials of a symmetric union and its partial knot. As a corollary, we obtain an inequality concerning their genera. It is known that there exists an epimorphism between their knot groups, and thus our inequality provides a positive answer to an old problem of Jonathan Simon in this case. Our formula also offers a useful condition to constrain possible symmetric union presentations of a given ribbon knot. It is an open question whether every ribbon knot is a symmetric union.

We define a family of discontinuous maps on the circle, called Bowen–Series-like maps, for geometric presentations of surface groups. The family has $2N$ parameters, where $2N$ is the number of generators of the presentation. We prove that all maps in the family have the same topological entropy, which coincides with the volume entropy of the group presentation. This approach allows a simple algorithmic computation of the volume entropy from the presentation only, using the Milnor–Thurston theory for one-dimensional maps.

Building on the correspondence between finitely axiomatised theories in Łukasiewicz logic and rational polyhedra, we prove that the unification type of the fragment of Łukasiewicz logic with $n\geqslant 2$ variables is nullary. This solves a problem left open by V. Marra and L. Spada [Ann. Pure Appl. Logic 164 (2013), pp. 192–210]. Furthermore, we refine the study of unification with bounds on the number of variables. Our proposal distinguishes the number m of variables allowed in the problem and the number n in the solution. We prove that the unification type of Łukasiewicz logic for all $m,n \geqslant 2$ is nullary.

We give a new criterion which guarantees that a free group admits a bi-ordering that is invariant under a given automorphism. As an application, we show that the fundamental group of the “magic manifold” is bi-orderable, answering a question of Kin and Rolfsen.

A pattern knot in a solid torus defines a self-map of the smooth knot concordance group. We prove that if the winding number of a pattern is even but not divisible by 8, then the corresponding map is not a homomorphism, thus partially establishing a conjecture of Hedden.

We solve generalizations of Hubbard’s twisted rabbit problem for analogs of the rabbit polynomial of degree $d\geq 2$. The twisted rabbit problem asks: when a certain quadratic polynomial, called the Douady rabbit polynomial, is twisted by a cyclic subgroup of a mapping class group, to which polynomial is the resulting map equivalent (as a function of the power of the generator)? The solution to the original quadratic twisted rabbit problem, given by Bartholdi and Nekrashevych, depended on the 4-adic expansion of the power of the mapping class by which we twist. In this paper, we provide a solution to a degree-d generalization that depends on the $d^2$-adic expansion of the power of the mapping class element by which we twist.

Given a symmetric monoidal category ${\mathcal C}$ with product $\sqcup $, where the neutral element for the product is an initial object, we consider the poset of $\sqcup $-complemented subobjects of a given object X. When this poset has finite height, we define decompositions and partial decompositions of X which are coherent with $\sqcup $, and order them by refinement. From these posets, we define complexes of frames and partial bases, augmented Bergman complexes and related ordered versions. We propose a unified approach to the study of their combinatorics and homotopy type, establishing various properties and relations between them. Via explicit homotopy formulas, we will be able to transfer structural properties, such as Cohen-Macaulayness.

In well-studied scenarios, the poset of $\sqcup $-complemented subobjects specializes to the poset of free factors of a free group, the subspace poset of a vector space, the poset of nondegenerate subspaces of a vector space with a nondegenerate form, and the lattice of flats of a matroid. The decomposition and partial decomposition posets, the complex of frames and partial bases together with the ordered versions, either coincide with well-known structures, generalize them, or yield new interesting objects. In these particular cases, we provide new results along with open questions and conjectures.

A subset of a finite set of filling curves on a surface is not necessarily filling. However, when a filling set spans homology and curves intersect pairwise at most once, it is shown that one can always add a curve and subtract a different curve to obtain a filling set that spans homology. A motivation for filling sets of curves that span homology comes from the Thurston spine and the Steinberg module of the mapping class group.

We study random walks on metric spaces with contracting isometries. In this first article of the series, we establish sharp deviation inequalities by adapting Gouëzel’s pivotal time construction. As an application, we establish the exponential bounds for deviation from below, central limit theorem, law of the iterated logarithms, and the geodesic tracking of random walks on mapping class groups and CAT(0) spaces.

This paper discusses variants of Weber’s class number problem in the spirit of arithmetic topology to connect the results of Sinnott–Kisilevsky and Kionke. Let p be a prime number. We first prove the p-adic convergence of class numbers in a ${\mathbb{Z}_{p}}$-extension of a global field and a similar result in a ${\mathbb{Z}_{p}}$-cover of a compact 3-manifold. Secondly, we establish an explicit formula for the p-adic limit of the p-power-th cyclic resultants of a polynomial using roots of unity of orders prime to p, the p-adic logarithm, and the Iwasawa invariants. Finally, we give thorough investigations of torus knots, twist knots, and elliptic curves; we complete the list of the cases with p-adic limits being in ${\mathbb{Z}}$ and find the cases such that the base p-class numbers are small and $\nu$’s are arbitrarily large.

Let M be a closed oriented 3-manifold equipped with an Euler structure e and an acyclic representation of its fundamental group. We define a twisted self-linking homology class of the diagonal of the two-point configuration space of M with respect to e. This twisted self-linking homology class appears as an obstruction in the Chern–Simons perturbation theory. When the representation is the maximal free abelian representation $\rho_0$, we prove that our self-linking class is a properly defined “logarithmic derivative” of the Reidemeister–Turaev torsion of $(M,\rho_0,e)$ equipped with the given Euler structure.

Kontsevich ([Kir95, Problem 3.48]) conjectured that $\mathrm {BDiff}(M, \text {rel }\partial )$ has the homotopy type of a finite CW complex for all compact $3$-manifolds with nonempty boundary. Hatcher-McCullough ([HM97]) proved this conjecture when M is irreducible. We prove a homological version of Kontsevich’s conjecture. More precisely, we show that $\mathrm {BDiff}(M, \text {rel }\partial )$ has finitely many nonzero homology groups each finitely generated when M is a connected sum of irreducible $3$-manifolds that each have a nontrivial and non-spherical boundary.

We show that the fundamental groups of smooth $4$-manifolds that admit geometric decompositions in the sense of Thurston have asymptotic dimension at most four, and equal to four when aspherical. We also show that closed $3$-manifold groups have asymptotic dimension at most three. Our proof method yields that the asymptotic dimension of closed $3$-dimensional Alexandrov spaces is at most three. Thus, we obtain that the Novikov conjecture holds for closed $4$-manifolds with such a geometric decomposition and for closed $3$-dimensional Alexandrov spaces. Consequences of these results include a vanishing result for the Yamabe invariant of certain $0$-surgered geometric $4$-manifolds and the existence of zero in the spectrum of aspherical smooth $4$-manifolds with a geometric decomposition.

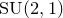We study the relative $\mathrm {SU}(2,1)$-character varieties of the one-holed torus, and the action of the mapping class group on them. We use an explicit description of the character variety of the free group of rank two in $\mathrm {SU}(2,1)$ in terms of traces, which allow us to describe the topology of the character variety. We then combine this description with a generalization of the Farey graph adapted to this new combinatorial setting, using ideas introduced by Bowditch. Using these tools, we can describe an open domain of discontinuity for the action of the mapping class group which strictly contains the set of convex cocompact characters, and we give several characterizations of representations in this domain.

We study the length of short cycles on uniformly random metric maps (also known as ribbon graphs) of large genus using a Teichmüller theory approach. We establish that, as the genus tends to infinity, the length spectrum converges to a Poisson point process with an explicit intensity. This result extends the work of Janson and Louf to the multi-faced case.

Let S be an orientable, connected surface of finite topological type, with genus $g \leqslant 2$, empty boundary and complexity at least 2; we prove that any graph endomorphism of the curve graph of S is actually an automorphism. Also, as a complement of the author’s previous results, we prove that under mild conditions on the complexity of the underlying surfaces, any graph morphism between curve graphs is induced by a homeomorphism of the surfaces.

To prove these results, we construct a finite subgraph whose union of iterated rigid expansions is the curve graph $\mathcal{C}(S)$. The sets constructed, and the method of rigid expansion, are closely related to Aramayona and Leininger’s finite rigid sets. We prove as a consequence that Aramayona and Leininger’s rigid set also exhausts $\mathcal{C}(S)$ via rigid expansions. The combinatorial rigidity results follow as an immediate consequence, based on the author’s previous results.

We consider a family of cyclic presentations and show that, subject to certain conditions on the defining parameters, they are spines of closed 3-manifolds. These are new examples where the reduced Whitehead graphs are of the same type as those of the Fractional Fibonacci presentations; here the corresponding manifolds are often (but not always) hyperbolic. We also express a lens space construction in terms of a class of positive cyclic presentations that are spines of closed 3-manifolds. These presentations then furnish examples where the Whitehead graphs are of the same type as those of the positive cyclic presentations of type $\mathfrak {Z}$, as considered by McDermott.

We study the problem of conjugating a diffeomorphism of the interval to (positive) powers of itself. Although this is always possible for homeomorphisms, the smooth setting is rather interesting. Besides the obvious obstruction given by hyperbolic fixed points, several other aspects need to be considered. As concrete results we show that, in class C1, if we restrict to the (closed) subset of diffeomorphisms having only parabolic fixed points, the set of diffeomorphisms that are conjugate to their powers is dense, but its complement is generic. In higher regularity, however, the complementary set contains an open and dense set. The text is complemented with several remarks and results concerning distortion elements of the group of diffeomorphisms of the interval in several regularities.

We study the behaviour of Kauffman bracket skein modules of 3-manifolds under gluing along surfaces. For this we extend this notion to $3$-manifolds with marking consisting of open intervals and circles in the boundary. The new module is called the stated skein module.

The first results concern non-injectivity of certain natural maps defined when forming connected sums along spheres or disks. These maps are injective for surfaces or for generic quantum parameter, but we show that in general they are not when the quantum parameter is a root of 1. We show that when the quantum parameter is a root of 1, the empty skein is zero in a connected sum where each constituent manifold has non-empty marking. We also prove various non-injectivity results for the Chebyshev-Frobenius map and the map induced by deleting marked balls.

We then interpret stated skein modules as a monoidal symmetric functor from a category of “decorated cobordisms” to a category of algebras and their bimodules. We apply this to deduce properties of stated skein modules as a Van-Kampen like theorem, a computation through Heegaard decompositions and a relation to Hochshild homology for trivial circle bundles over surfaces.