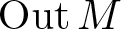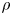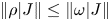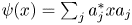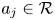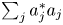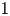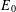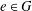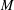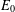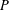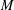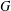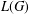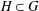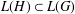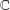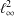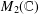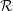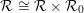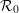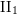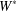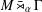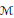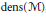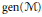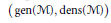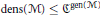Refine search
Actions for selected content:
21 results
QUANTUM EXPANDERS AND QUANTIFIER REDUCTION FOR TRACIAL VON NEUMANN ALGEBRAS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 04 July 2025, pp. 1-37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Every locally compact group is the outer automorphism group of a II1 factor
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 March 2025, pp. 1-12
-
- Article
- Export citation
DYNAMICAL MCDUFF-TYPE PROPERTIES FOR GROUP ACTIONS ON VON NEUMANN ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 02 April 2024, pp. 2593-2629
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Corrigendum: Von Neumann algebras and extensions of inverse semigroups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 3 / August 2023
- Published online by Cambridge University Press:
- 22 August 2023, pp. 919-922
-
- Article
-
- You have access
- HTML
- Export citation
Which states can be reached from a given state by unital completely positive maps?
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 3 / August 2022
- Published online by Cambridge University Press:
- 05 July 2022, pp. 632-651
-
- Article
- Export citation
MEASURABLE
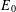 $E_{0}$-SEMIGROUPS ARE CONTINUOUS
$E_{0}$-SEMIGROUPS ARE CONTINUOUS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 04 December 2019, pp. 278-288
- Print publication:
- October 2021
-
- Article
- Export citation
Ozawa's class 𝒮 for locally compact groups and unique prime factorization of group von Neumann algebras
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 19 July 2019, pp. 2656-2681
- Print publication:
- October 2020
-
- Article
- Export citation
A VON NEUMANN ALGEBRA CHARACTERIZATION OF PROPERTY (T) FOR GROUPOIDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 21 December 2018, pp. 363-386
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
LEFT SYMMETRIC POINTS FOR BIRKHOFF ORTHOGONALITY IN THE PREDUALSOF VON NEUMANN ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 28 August 2018, pp. 494-501
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
Stability of products of equivalence relations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 9 / September 2018
- Published online by Cambridge University Press:
- 17 August 2018, pp. 2005-2019
- Print publication:
- September 2018
-
- Article
- Export citation
A Note on Uniformly Bounded Cocycles into Finite Von Neumann Algebras
-
- Journal:
- Canadian Mathematical Bulletin / Volume 61 / Issue 2 / 01 June 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 236-239
- Print publication:
- 01 June 2018
-
- Article
-
- You have access
- Export citation
WEAK HAAGERUP PROPERTY OF
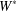 $W^{\ast }$ -CROSSED PRODUCTS
$W^{\ast }$ -CROSSED PRODUCTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 31 August 2017, pp. 119-126
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
Von Neumann Algebras and Extensions of Inverse Semigroups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 19 September 2016, pp. 57-97
-
- Article
- Export citation
From Quantum Groups to Groups
-
- Journal:
- Canadian Journal of Mathematics / Volume 65 / Issue 5 / 01 October 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1073-1094
- Print publication:
- 01 October 2013
-
- Article
-
- You have access
- Export citation
On Cardinal Invariants and Generators for von Neumann Algebras
-
- Journal:
- Canadian Journal of Mathematics / Volume 64 / Issue 2 / 16 April 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 455-480
- Print publication:
- 16 April 2012
-
- Article
-
- You have access
- Export citation
KK-Theory and Spectral Flow in von Neumann Algebras
-
- Journal:
- Journal of K-Theory / Volume 10 / Issue 2 / October 2012
- Published online by Cambridge University Press:
- 04 April 2012, pp. 241-277
- Print publication:
- October 2012
-
- Article
- Export citation
TYPE DECOMPOSITION OF A PSEUDOEFFECT ALGEBRA
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 89 / Issue 3 / December 2010
- Published online by Cambridge University Press:
- 28 February 2011, pp. 335-358
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
On the equational theory of projection lattices of finite von neumann factors
-
- Journal:
- The Journal of Symbolic Logic / Volume 75 / Issue 3 / September 2010
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1102-1110
- Print publication:
- September 2010
-
- Article
- Export citation
SPECTRAL FLOW AND WINDING NUMBER IN VON NEUMANN ALGEBRAS
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 7 / Issue 3 / July 2008
- Published online by Cambridge University Press:
- 27 February 2008, pp. 589-619
- Print publication:
- July 2008
-
- Article
- Export citation
On certain pairs of automorphisms of rings
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 54 / Issue 1 / February 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 29-38
- Print publication:
- February 1993
-
- Article
-
- You have access
- Export citation