Refine search
Actions for selected content:
4 results
ON THE RANK OF A VERBAL SUBGROUP OF A FINITE GROUP
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 12 May 2021, pp. 145-159
- Print publication:
- October 2022
-
- Article
-
- You have access
- Open access
- Export citation
A NILPOTENCY CRITERION FOR SOME VERBAL SUBGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 27 February 2019, pp. 281-289
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
ON GROUPS WITH FINITE CONJUGACY CLASSES IN A VERBAL SUBGROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 08 June 2017, pp. 429-437
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
A problem of expressibility in some amalgamated products of groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 1 / August 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 105-115
- Print publication:
- August 2001
-
- Article
-
- You have access
- Export citation
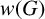
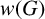

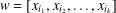
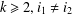
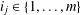
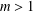
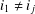
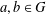
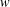
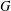
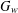
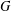
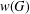
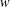
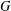
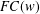
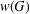
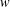
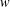
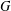
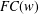
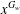
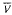 (
(