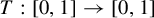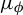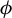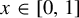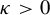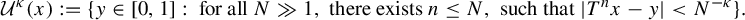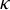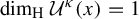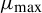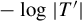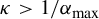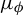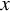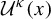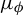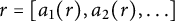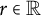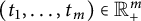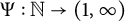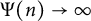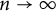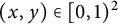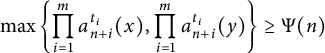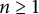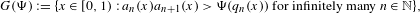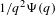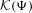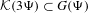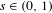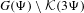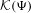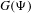Refine search
Actions for selected content:
5 results
Uniform Diophantine approximation and run-length function in continued fractions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 30 September 2024, pp. 1246-1280
- Print publication:
- April 2025
-
- Article
- Export citation
Uniform approximation problems of expanding Markov maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 15 February 2023, pp. 159-183
- Print publication:
- January 2024
-
- Article
- Export citation
A note on the relative growth of products of multiple partial quotients in the plane
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 19 August 2022, pp. 544-552
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
METRICAL PROBLEMS IN DIOPHANTINE APPROXIMATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 26 July 2021, pp. 519-521
- Print publication:
- December 2021
-
- Article
-
- You have access
- HTML
- Export citation
The sets of Dirichlet non-improvable numbers versus well-approximable numbers
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 27 June 2019, pp. 3217-3235
- Print publication:
- December 2020
-
- Article
- Export citation