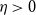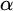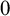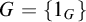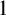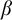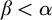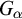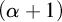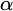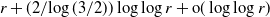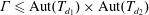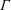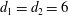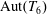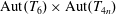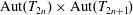Refine search
Actions for selected content:
50 results
12 - Regression and Classification
-
- Book:
- Probability and Statistics for Data Science
- Published online:
- 19 June 2025
- Print publication:
- 03 July 2025, pp 495-598
-
- Chapter
- Export citation
Critical scaling profile for trees and connected subgraphs on the complete graph
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 11 June 2025, pp. 1-16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Differential Ordering of Objects and Attributes
-
- Journal:
- Psychometrika / Volume 51 / Issue 2 / June 1986
- Published online by Cambridge University Press:
- 01 January 2025, pp. 209-240
-
- Article
- Export citation
Tree universality in positional games
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 13 December 2024, pp. 338-358
-
- Article
- Export citation
ON THE RAMSEY NUMBERS OF TREE GRAPHS VERSUS CERTAIN GENERALISED WHEEL GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 08 October 2024, pp. 564-565
- Print publication:
- December 2024
-
- Article
-
- You have access
- HTML
- Export citation
Antidirected subgraphs of oriented graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 06 March 2024, pp. 446-466
-
- Article
- Export citation
A HIERARCHY ON NON-ARCHIMEDEAN POLISH GROUPS ADMITTING A COMPATIBLE COMPLETE LEFT-INVARIANT METRIC
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 06 February 2024, pp. 1-19
-
- Article
- Export citation
DEDEKIND-FINITE CARDINALS HAVING COUNTABLE PARTITIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 17 July 2023, pp. 1308-1323
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Calling time on the imperial lawn and the imperative for greenhouse gas mitigation
-
- Journal:
- Global Sustainability / Volume 6 / 2023
- Published online by Cambridge University Press:
- 06 January 2023, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cover time for branching random walks on regular trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 09 February 2022, pp. 256-277
- Print publication:
- March 2022
-
- Article
- Export citation
APPROXIMATING TREES AS COLOURED LINEAR ORDERS AND COMPLETE AXIOMATISATIONS OF SOME CLASSES OF TREES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 08 June 2021, pp. 1035-1065
- Print publication:
- September 2021
-
- Article
- Export citation
Conserving the Critically Endangered tree Vatica cauliflora: population and conservation status assessment
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE AUTOMORPHISM GROUP OF THE UNIVERSAL HOMOGENEOUS MEET-TREE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 01 February 2021, pp. 1508-1540
- Print publication:
- December 2021
-
- Article
- Export citation
7 - Skeletons and Life
- from Part II - Life Here, Implications for Elsewhere
-
- Book:
- The Biological Universe
- Published online:
- 24 September 2020
- Print publication:
- 24 September 2020, pp 101-117
-
- Chapter
- Export citation
A CLASS OF SMALL DEVIATION THEOREMS FOR FUNCTIONALS OF RANDOM FIELDS ON A TREE WITH UNIFORMLY BOUNDED DEGREE IN RANDOM ENVIRONMENT
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 36 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 24 August 2020, pp. 169-183
-
- Article
- Export citation
6 - Multiple Boundary Representations of λ-Harmonic Functions on Trees
-
-
- Book:
- Analysis and Geometry on Graphs and Manifolds
- Published online:
- 14 August 2020
- Print publication:
- 20 August 2020, pp 95-125
-
- Chapter
- Export citation
A tree species with an extremely small population: recategorizing the Critically Endangered Acer yangbiense
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
7 - The Graph Conception
-
- Book:
- Conceptions of Set and the Foundations of Mathematics
- Published online:
- 09 January 2020
- Print publication:
- 23 January 2020, pp 184-217
-
- Chapter
- Export citation
New Simple Lattices in Products of Trees and their Projections
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 07 October 2019, pp. 1624-1690
- Print publication:
- December 2020
-
- Article
- Export citation
THE GENERALIZED ENTROPY ERGODIC THEOREM FOR NONHOMOGENEOUS MARKOV CHAINS INDEXED BY A HOMOGENEOUS TREE
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 34 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 30 January 2019, pp. 221-234
-
- Article
- Export citation