Refine search
Actions for selected content:
11 results
3 - Flat Torsors in Complex Geometry
-
-
- Book:
- Moduli, Motives and Bundles
- Published online:
- 31 October 2025
- Print publication:
- 20 November 2025, pp 106-142
-
- Chapter
- Export citation
Non-formality of Galois cohomology modulo all primes
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 12 August 2025, pp. 831-858
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Positivity of Hodge bundles of abelian varieties over some function fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 9 / September 2021
- Published online by Cambridge University Press:
- 03 August 2021, pp. 1964-2000
- Print publication:
- September 2021
-
- Article
- Export citation
RIGIDIFIED TORSOR COCYCLES, HYPERCOVERINGS AND BUNDLE GERBES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 07 April 2020, pp. 115-144
- Print publication:
- February 2022
-
- Article
- Export citation
On a purely inseparable analogue ofthe Abhyankar conjecture for affine curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 8 / August 2018
- Published online by Cambridge University Press:
- 19 July 2018, pp. 1633-1658
- Print publication:
- August 2018
-
- Article
- Export citation
Octonion Algebras over Rings Are Not Determined by their Norms
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 2 / 14 June 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 303-309
- Print publication:
- 14 June 2014
-
- Article
-
- You have access
- Export citation
On the Notion of Visibility of Torsors
-
- Journal:
- Canadian Mathematical Bulletin / Volume 56 / Issue 2 / 01 June 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 225-228
- Print publication:
- 01 June 2013
-
- Article
-
- You have access
- Export citation
Rationally trivial torsors in
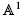 -homotopy theory
-homotopy theory
-
- Journal:
- Journal of K-Theory / Volume 7 / Issue 3 / June 2011
- Published online by Cambridge University Press:
- 16 May 2011, pp. 541-572
- Print publication:
- June 2011
-
- Article
- Export citation
The canonical subgroup for families of abelian varieties
-
- Journal:
- Compositio Mathematica / Volume 143 / Issue 3 / May 2007
- Published online by Cambridge University Press:
- 04 December 2007, pp. 566-602
- Print publication:
- May 2007
-
- Article
-
- You have access
- Export citation
Invariants de classes : le cas semi-stable
-
- Journal:
- Compositio Mathematica / Volume 141 / Issue 4 / July 2005
- Published online by Cambridge University Press:
- 21 June 2005, pp. 887-901
- Print publication:
- July 2005
-
- Article
-
- You have access
- Export citation
Non-abelian Cohomology and Rational Points
-
- Journal:
- Compositio Mathematica / Volume 130 / Issue 3 / February 2002
- Published online by Cambridge University Press:
- 04 December 2007, pp. 241-273
- Print publication:
- February 2002
-
- Article
-
- You have access
- Export citation















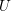
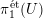
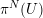
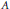
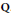
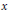
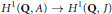
 -homotopy theory
-homotopy theory
